题解 LOJ3275 「JOISC 2020 Day2」有趣的 Joitter 交友
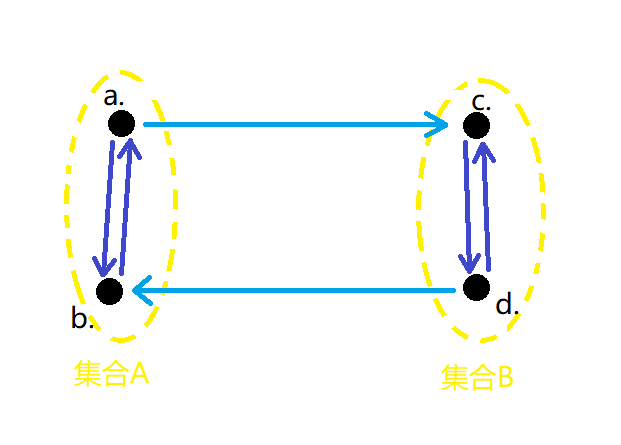
把两个互相关注的人缩成一个集合。如果对于两个集合A,B,集合A中某个人关注了集合B中的某个人,集合B中的某个人也关注了集合A中的某个人(这四个人可以互不相同),则把A,B缩成一个大集合。以此类推。例如下图中,原有A,B两个集合,后来加入了\(a\rightarrow c\), \(d\rightarrow b\)两条边。此时如果搞活动,会带来\(a\rightarrow d\), \(d\rightarrow a\)两新的条边。接下来会有连锁反应,其结果是\(a\),\(b\),\(c\),\(d\)两两相互关注。这就是为什么我们可以把图缩成若干个“集合”,然后直接在集合间连边。
考虑一个集合\(S\),大小为\(sz(S)\)。如果有\(ine(S)\)条边连向这个集合(连向集合内的至少一个点),则集合\(S\)对答案的贡献是:\(sz(S)(sz(S)-1)+sz(S)ine(S)\)。
我们用并查集维护这些集合。用\(\texttt{set}\)维护连向每个集合的边\(ine\)。
考虑如何处理加边操作。加入一条边\(x\rightarrow y\)时,分三种情况讨论:
- 如果\(x\),\(y\)已经在同一个集合内,则什么都不用做。
- 如果\(y\)所在集合已经有了连向\(x\)所在集合的边,则把两个点所在集合合并。
- 其他情况下,更新\(y\)所在集合的\(ine\)即可。
发现要判断:\(y\)所在集合是否有连向\(x\)所在集合的边。我们给每个集合再开两个\(\texttt{set}\),记录这个集合的入边、出边。注意这里的“出/入边”指的是集合之间的边。
合并两个集合时,用启发式合并。维护好每个集合相关信息的若干个\(\texttt{set}\)即可。注意,合并时可能会造成连锁反应,所以我们用一个队列,只要队列不为空,就不断取出队头,进行合并。
时间复杂度\(O(n\log^2n)\)。
参考代码:
//problem:LOJ3275
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
namespace Fread{
const int MAXN=1<<20;
char buf[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buf)+fread(buf,1,MAXN,stdin);
if(S==T)return EOF;
}
return *S++;
}
}//namespace Fread
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
template<typename T>inline void read(T& x){
x=0;int f=1;
char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch))x=x*10+(ch-'0'),ch=getchar();
x*=f;
}
/* ------ by:duyi ------ */ // myt天下第一
const int MAXN=1e5;
int n,m,fa[MAXN+5];
ll ans;
set<int>points[MAXN+5],ine[MAXN+5],inp[MAXN+5],outp[MAXN+5];
queue<pii>q;
int get_fa(int x){return x==fa[x]?x:(fa[x]=get_fa(fa[x]));}
inline ll calc(int x){
return (ll)points[x].size()*(points[x].size()-1)+(ll)ine[x].size()*points[x].size();
}
void _merge(int x,int y){
x=get_fa(x);y=get_fa(y);if(x==y)return;
// y -> x
if(points[x].size()<points[y].size())swap(x,y);
fa[y]=x;ans-=calc(x);ans-=calc(y);
if(inp[x].count(y))inp[x].erase(y);
if(outp[x].count(y))outp[x].erase(y);
for(set<int>::iterator it=points[y].begin();it!=points[y].end();++it){
int v=(*it);
points[x].insert(v);
if(ine[x].count(v))ine[x].erase(v);
}
for(set<int>::iterator it=ine[y].begin();it!=ine[y].end();++it){
int v=(*it);
if(!points[x].count(v)){
ine[x].insert(v);
}
}
for(set<int>::iterator it=inp[y].begin();it!=inp[y].end();++it){
int v=(*it);
if(v!=x){
outp[v].erase(y);
outp[v].insert(x);
if(outp[x].count(v)){
q.push(mk(x,v));
}
else inp[x].insert(v);
}
}
for(set<int>::iterator it=outp[y].begin();it!=outp[y].end();++it){
int v=(*it);
if(v!=x){
inp[v].erase(y);
inp[v].insert(x);
if(inp[x].count(v)){
q.push(mk(x,v));
}
else outp[x].insert(v);
}
}
ans+=calc(x);
}
void merge_points(){
while(!q.empty()){
int x=q.front().fi,y=q.front().se;
q.pop();_merge(x,y);
}
}
int main() {
read(n);read(m);
for(int i=1;i<=n;++i)fa[i]=i,points[i].insert(i);
while(m--){
int x,y;read(x);read(y);
if(get_fa(x)==get_fa(y)){printf("%lld\n",ans);continue;}
if(inp[get_fa(x)].count(get_fa(y))){
q.push(mk(x,y));
merge_points();
}
else if(!ine[get_fa(y)].count(x)){
ans-=calc(get_fa(y));
ine[get_fa(y)].insert(x);
inp[get_fa(y)].insert(get_fa(x));
outp[get_fa(x)].insert(get_fa(y));
ans+=calc(get_fa(y));
}
printf("%lld\n",ans);
}
return 0;
}

