LOJ3277 「JOISC 2020 Day3」星座 3
LOJ3277 「JOISC 2020 Day3」星座 3
题目大意
建议直接阅读原题题面。
本题题解
考虑一个区间,初始时为\([1,n]\)。每次找出区间中楼房的最大高度\(mx\)。高度为\(mx\)的这些楼房把区间划分为了若干段,我们继续递归每一段。递归的边界是区间内所有楼房高度相同时不再递归。这样,我们就建出了一个有\(O(n)\)个节点的树形结构,因为我们是根据区间最大值来划分区间,所以可以认为建出的树是一棵广义的笛卡尔树(虽然它并不是二叉树)。
根据题目中“不能存在星座”的要求,发现:对于笛卡尔树的每个区间,它上方的区域(也就是下图中蓝色框框柱的区域,以下简称蓝色区域),要么一颗星星都没有,要么只保留一颗星星。因为只要数量超过\(1\)颗,就一定会冲突。不过这只是必要条件,并不充分,因为蓝色区域里的星星,可能和下面(儿子里的)星星在同一个长方形中。所以我们将通过 DP 进行更复杂的决策。
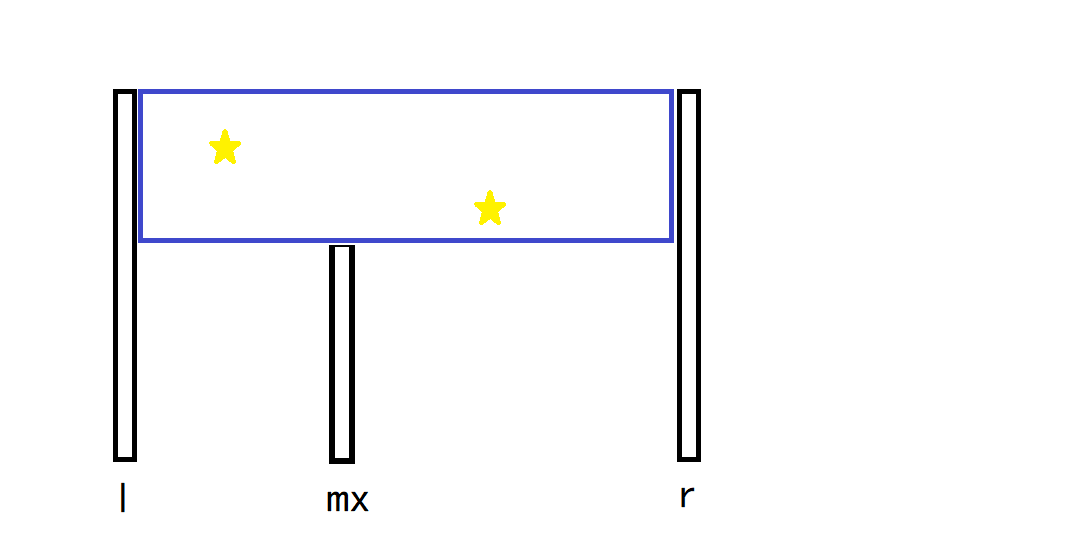
设\(f[l,r]\)表示笛卡尔树上\([l,r]\)这个节点,只考虑它的儿子和蓝色区域内的星星,需要删除的星星的代价之和的最小值。
可以发现,一个节点的各个儿子之间是互不相关的。
每个节点的转移,分为:(1)蓝色区域内一颗星星都没有 (2)蓝色区域内只保留一颗星星,这两种情况。
-
当蓝色区域内一颗星星都没有时,我们只需要把各个儿子的\(f\)值相加,再加上删除蓝色区域内所有星星的代价即可。
-
如果要在蓝色区域内保留一颗星星,我们枚举保留哪一颗。当保留某一颗星星时,这颗星星下方的子树会受到限制(可以结合样例2理解)。
首先,对于照片的每一列,也就是每一个\(x\)坐标,一定有一个包含它的,且深度最大的节点,我们记这个节点为\(p[x]\)。
发现,如果我们要保留的星星横坐标为\(x\),则笛卡尔树上,\(p[x]\)到当前节点的这一条链上,每个节点的蓝色区域内的星星都必须全部删除。如下图(黑色节点表示这个节点蓝色区域内的星星被全部删除):
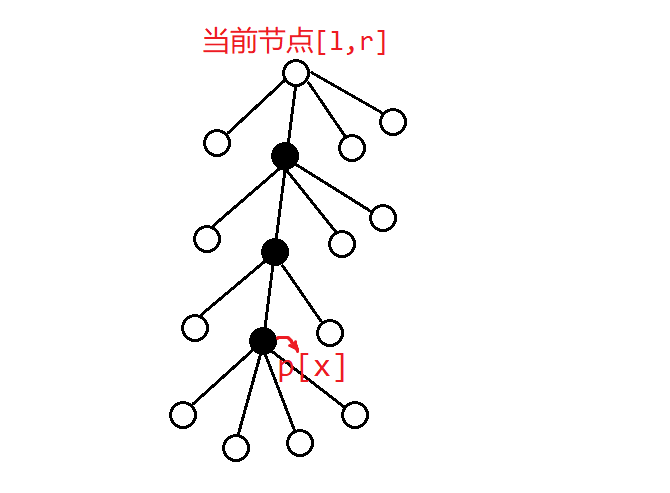
因此我们对每个节点,维护一个\(g[l,r]\),表示强制只进行第(1)种转移的代价,和进行第(2)种转移的代价的差。那么\(f[l,r]\)的第二种转移,就相当于只进行第一种转移的代价,减去要保留的这颗星星的\(c_i\),再加上从\([l,r]\)到\(p[x]\)的这条链上的节点的\(g\)的和。
求树上一条链的和,可以用树链剖分实现。
到这里这道题的主要思路基本讲完了。还有一个实现上的小问题,就是怎么把每颗星星,精准定位到笛卡尔树上某个节点的蓝色区域里。我们可以线段树上二分,找到这颗星星左边第一个高度大于等于该星星\(y\)的楼房,右边第一个高度大于等于该星星\(y\)的楼房,这两幢楼房之间,一定是笛卡尔树上的一个节点,把该星星放到这个节点的蓝色区域内就好了。
时间复杂度\(O(m\log n+n\log^2n)\)。分别是线段树上二分和树链剖分的复杂度。
参考代码
//problem:LOJ3277
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
namespace Fread{
const int MAXN=1<<20;
char buf[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buf)+fread(buf,1,MAXN,stdin);
if(S==T)return EOF;
}
return *S++;
}
}//namespace Fread
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
inline int read(){
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
/* ------ by:duyi ------ */ // myt天下第一
const int MAXN=2e5,MAXC=1e9;
const ll INF=0x3f3f3f3f3f3f3f3f;
int n,m,a[MAXN+5];
struct stars{int x,y,c,l,r;}b[MAXN+5];
struct SegmentTree{
int mx[MAXN*4+5],mxp[MAXN*4+5];
void push_up(int p){
if(mx[p<<1]>=mx[p<<1|1]){
mx[p]=mx[p<<1];
mxp[p]=mxp[p<<1];
}
else{
mx[p]=mx[p<<1|1];
mxp[p]=mxp[p<<1|1];
}
}
void build(int p,int l,int r){
if(l==r){
mx[p]=a[l];
mxp[p]=l;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
push_up(p);
}
pii query(int p,int l,int r,int ql,int qr){
if(ql<=l&&qr>=r)return mk(mx[p],mxp[p]);
int mid=(l+r)>>1;
pii res=mk(0,0);
if(ql<=mid)res=query(p<<1,l,mid,ql,qr);
if(qr>mid){pii t=query(p<<1|1,mid+1,r,ql,qr);if(t.fst>res.fst)res=t;}
return res;
}
int _nxt_geq(int p,int l,int r,int v){
if(l==r){assert(mx[p]>=v);return l;}
int mid=(l+r)>>1;
if(mx[p<<1]>=v)return _nxt_geq(p<<1,l,mid,v);
else return _nxt_geq(p<<1|1,mid+1,r,v);
}
int nxt_geq(int p,int l,int r,int pos,int v){
if(mx[p]<v)return n+1;
if(l>=pos)return _nxt_geq(p,l,r,v);
int mid=(l+r)>>1,res=n+1;
if(pos<=mid)res=nxt_geq(p<<1,l,mid,pos,v);
if(res!=n+1)return res;
else return nxt_geq(p<<1|1,mid+1,r,pos,v);
}
int _pre_geq(int p,int l,int r,int v){
if(l==r){assert(mx[p]>=v);return l;}
int mid=(l+r)>>1;
if(mx[p<<1|1]>=v)return _pre_geq(p<<1|1,mid+1,r,v);
else return _pre_geq(p<<1,l,mid,v);
}
int pre_geq(int p,int l,int r,int pos,int v){
if(mx[p]<v)return 0;
if(r<=pos)return _pre_geq(p,l,r,v);
int mid=(l+r)>>1,res=0;
if(pos>mid)res=pre_geq(p<<1|1,mid+1,r,pos,v);
if(res)return res;
else return pre_geq(p<<1,l,mid,pos,v);
}
SegmentTree(){}
}T;
map<pii,int>id;
pii rev[MAXN+5];
int cnt,p[MAXN+5];
vector<int>pos[MAXN+5],G[MAXN+5];
void build_tree(int l,int r){
//cout<<"solve "<<l<<" "<<r<<endl;
id[mk(l,r)]=++cnt;
int u=cnt;
rev[u]=mk(l,r);
int mx=T.query(1,1,n,l,r).fst;
int lb=l;
while(lb<=r){
pii t=T.query(1,1,n,lb,r);
if(t.fst!=mx)break;
pos[u].pb(t.scd);
lb=t.scd+1;
}
if(pos[u].size()==r-l+1){
for(int i=l;i<=r;++i)p[i]=u;
return;
}
pos[u].pb(r+1);
int lst=l-1;
for(int i=0;i<(int)pos[u].size();++i){
if(i!=pos[u].size()-1)p[pos[u][i]]=u;
if(lst+1!=pos[u][i]){
build_tree(lst+1,pos[u][i]-1);
G[u].pb(id[mk(lst+1,pos[u][i]-1)]);
}
lst=pos[u][i];
}
pos[u].pop_back();
}
int fa[MAXN+5],son[MAXN+5],sz[MAXN+5],dep[MAXN+5];
void dfs1(int u){
dep[u]=dep[fa[u]]+1;
sz[u]=1;
for(int i=0;i<(int)G[u].size();++i){
int v=G[u][i];
fa[v]=u;
dfs1(v);
sz[u]+=sz[v];
if(!son[u]||sz[v]>sz[son[u]])son[u]=v;
}
}
int top[MAXN+5],dfn[MAXN+5];
void dfs2(int u,int t){
top[u]=t;dfn[u]=++cnt;
if(son[u])dfs2(son[u],t);
for(int i=0;i<(int)G[u].size();++i){
int v=G[u][i];
if(v==son[u])continue;
dfs2(v,v);
}
}
struct FenwickTree{
//单点修改区间查询
ll c[MAXN+5];
ll query(int p){
ll res=0;
for(;p;p-=(p&(-p)))res+=c[p];
return res;
}
ll query(int l,int r){
return query(r)-query(l-1);
}
void modify(int p,ll v){
for(;p<=n;p+=(p&(-p)))c[p]+=v;
}
FenwickTree(){}
}F;
ll query(int v,int goal){
if(v==goal)return 0;
ll res=0;
while(top[v]!=top[goal]){
res+=F.query(dfn[top[v]],dfn[v]);
v=fa[top[v]];
}
if(v==goal)return res;
res+=F.query(dfn[goal]+1,dfn[v]);
return res;
}
void add(int u,ll val){
F.modify(dfn[u],val);
}
vector<int>vec[MAXN+5];
ll s[MAXN+5],f[MAXN+5],g[MAXN+5];
void solve(int l,int r){
int u=id[mk(l,r)];
//cout<<"solve "<<l<<" "<<r<<" "<<s[u]<<endl;
if(pos[u].size()==r-l+1){
f[u]=s[u];
for(int i=0;i<(int)vec[u].size();++i){
f[u]=min(f[u],s[u]-b[vec[u][i]].c);
}
g[u]=s[u]-f[u];
add(u,g[u]);
return;
}
pos[u].pb(r+1);
int lst=l-1;
ll sum=s[u];
for(int i=0;i<(int)pos[u].size();++i){
if(lst+1!=pos[u][i]){
solve(lst+1,pos[u][i]-1);
sum+=f[id[mk(lst+1,pos[u][i]-1)]];
}
lst=pos[u][i];
}
f[u]=sum;//上方星座全部删除
for(int i=0;i<(int)vec[u].size();++i){//上方星座保留一个
f[u]=min(f[u],sum-b[vec[u][i]].c+query(p[b[vec[u][i]].x],u));
}
g[u]=sum-f[u];
add(u,g[u]);
}
int main() {
//freopen("data.in","r",stdin);
n=read();
for(int i=1;i<=n;++i)a[i]=read();
T.build(1,1,n);build_tree(1,n);
m=read();
for(int i=1;i<=m;++i){
b[i].x=read(),b[i].y=read(),b[i].c=read();
b[i].l=T.pre_geq(1,1,n,b[i].x,b[i].y)+1;
b[i].r=T.nxt_geq(1,1,n,b[i].x,b[i].y)-1;
assert(id.count(mk(b[i].l,b[i].r)));
vec[id[mk(b[i].l,b[i].r)]].pb(i);
s[id[mk(b[i].l,b[i].r)]]+=b[i].c;
}
cnt=0;dfs1(1);dfs2(1,1);
solve(1,n);
cout<<f[id[mk(1,n)]]<<endl;
return 0;
}


