实验三:朴素贝叶斯算法实验
【实验目的】
理解朴素贝叶斯算法原理,掌握朴素贝叶斯算法框架。
【实验内容】
针对下表中的数据,编写python程序实现朴素贝叶斯算法(不使用sklearn包),对输入数据进行预测;
熟悉sklearn库中的朴素贝叶斯算法,使用sklearn包编写朴素贝叶斯算法程序,对输入数据进行预测;
【实验报告要求】
对照实验内容,撰写实验过程、算法及测试结果;
代码规范化:命名规则、注释;
查阅文献,讨论朴素贝叶斯算法的应用场景。
| 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
| 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 碍滑 | 是 |
| 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 碍滑 | 是 |
| 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 碍滑 | 是 |
| 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 碍滑 | 是 |
| 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 碍滑 | 是 |
| 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
一、编写python程序实现朴素贝叶斯算法(不使用sklearn包)
1.
#输入数据集 datasets=[['青绿','蜷缩','浊响','清晰','凹陷','碍滑','是'], ['乌黑','蜷缩','沉闷','清晰','凹陷','碍滑','是'], ['乌黑','蜷缩','浊响','清晰','凹陷','碍滑','是'], ['青绿','蜷缩','沉闷','清晰','凹陷','碍滑','是'], ['浅白','蜷缩','浊响','清晰','凹陷','碍滑','是'], ['青绿','稍蜷','浊响','清晰','稍凹','软粘','是'], ['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','是'], ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','是'], ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','否'], ['青绿','硬挺','清脆','清晰','平坦','软粘','否'], ['浅白','硬挺','清脆','模糊','平坦','硬滑','否'], ['浅白','蜷缩','浊响','模糊','平坦','软粘','否'], ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','否'], ['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','否'], ['乌黑','稍蜷','浊响','清晰','稍凹','软粘','否'], ['浅白','蜷缩','浊响','模糊','平坦','硬滑','否'], ['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','否'] ]
2.
#数据集标签特征 labels=['色泽','根蒂','敲声','纹理','脐部','触感','好瓜']
3.
import pandas as pd #将数据集转换为DataFrame数据 data=pd.DataFrame(datasets,columns=labels)
4.
#样本数据 data

5.
# 计算样本数据集分类标签为是/否的概率 # data为样本数据和分类结果;cls_val是分类字符,是/否 #求先验概率函数 def prob1(data,cls_val): cnt=0.0 for index,row in data.iterrows(): if row[-1]==cls_val: cnt+=1 return cnt/len(data) # 统计每种属性的取值可能,拉普拉斯修正用 def prob2(data,cls_val): cnt=0.0 for index,row in data.iterrows(): if row[-1]==cls_val: cnt+=1 return (cnt+1)/(len(data)+len(set(data['好瓜']))) # 计算条件概率 # data为样本数据和分类结果;cls_val是分类字符,是/否;attr_index是属性的序号;attr_val是属性的取值;s是属性的特征数目 def conditionp1(data,cls_val,attr_index,attr_val): cnt1=0.0 cnt2=0.0 for index,row in data.iterrows(): if row[-1]==cls_val: cnt1+=1 if row[attr_index]==attr_val: cnt2+=1 return cnt2/cnt1 # 统计每种属性的取值可能,拉普拉斯修正用 def conditionp2(data,cls_val,attr_index,attr_val,s): cnt1=0.0 cnt2=0.0 for index,row in data.iterrows(): if row[-1]==cls_val: cnt1+=1 if row[attr_index]==attr_val: cnt2+=1 return (cnt2+1)/(cnt1+s) # 利用后验概率计算先验概率 # data为样本数据和分类结果;testlist是新样本数据列表;cls_y、cls_n是分类字符,是/否;s是属性的特征数目 def nb(data,testlist,cls_y,cls_n): py=prob1(data,cls_y) pn=prob1(data,cls_n) for i,val in enumerate(testlist): py*=conditionp1(data,cls_y,i,val) pn*=conditionp1(data,cls_n,i,val) if (py==0) or (pn==0): py=prob2(data,cls_y) pn=prob2(data,cls_n) for i,val in enumerate(testlist): s=len(set(data[data.columns[i]])) py*=conditionp2(data,cls_y,i,val,s) pn*=conditionp2(data,cls_n,i,val,s) if py>pn: result=cls_y else: result=cls_n return {cls_y:py,cls_n:pn,'好瓜':result}
6.
#测试 tsvec = ['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑'] prob = nb(data,tsvec,'是','否') print("测试结果:",prob)

二、使用sklearn包编写朴素贝叶斯算法程序
1.
#输入数据集 datasets1=[['0','0','0','0','0','0','1'], ['1','0','1','0','0','0','1'], ['1','0','0','0','0','0','1'], ['0','0','1','0','0','0','1'], ['2','0','0','0','0','0','1'], ['0','1','0','0','1','1','1'], ['1','1','0','1','1','1','1'], ['1','1','0','0','1','2','1'], ['1','1','1','1','1','2','0'], ['0','2','2','0','2','1','0'], ['2','2','2','2','2','2','0'], ['2','0','0','2','2','1','0'], ['0','1','0','1','0','2','0'], ['2','1','1','1','0','2','0'], ['1','1','0','0','1','1','0'], ['2','0','0','2','2','2','0'], ['0','0','1','1','1','2','0'] ] #青绿:0 乌黑:1 浅白:2 # 蜷缩 0 稍蜷 1 硬挺 2 # 浊响 0 沉闷 1 清脆 2 # 清晰 0 稍糊 1 模糊 2 # 凹陷 0 稍凹 1 平坦 2 # 碍滑 0 软粘 1 硬滑 2 # 是 1 否 0 labels=['色泽','根蒂','敲声','纹理','脐部','触感','好瓜']
2.
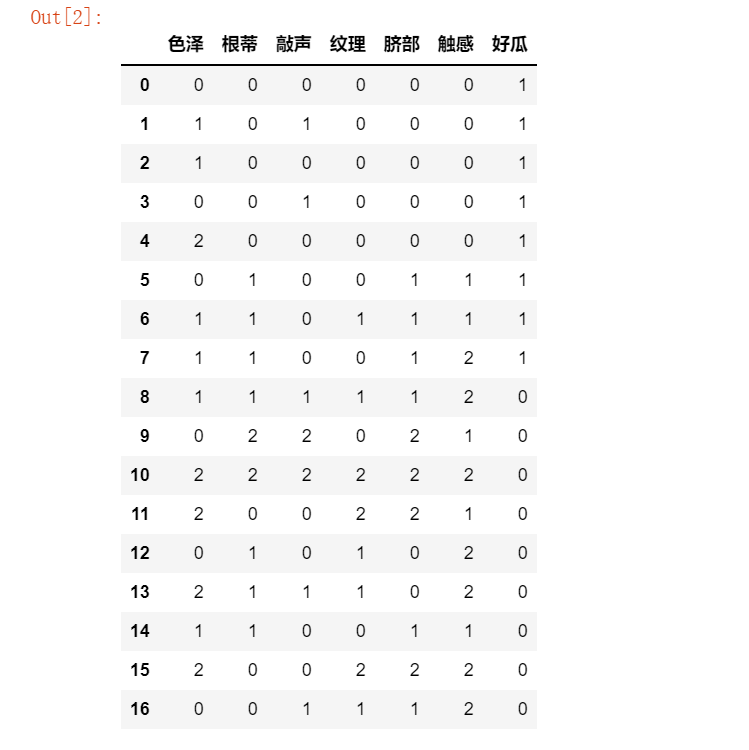
#样本数据 import pandas as pd #将数据集转换为DataFrame数据 data1=pd.DataFrame(datasets1,columns=labels) data1
3.
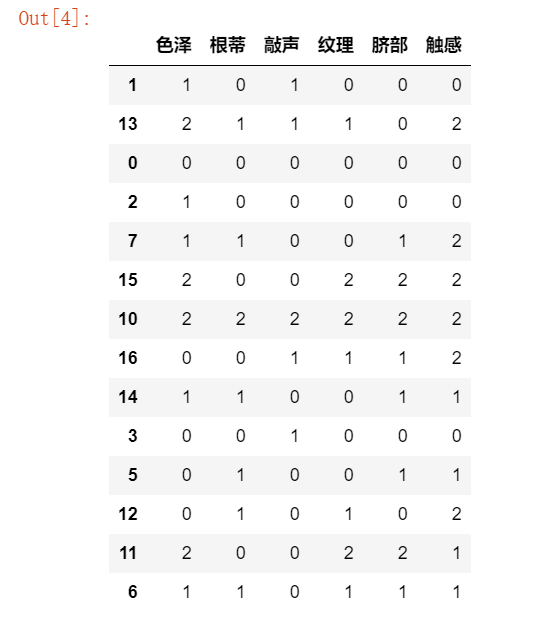
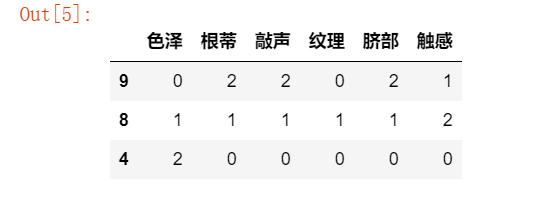
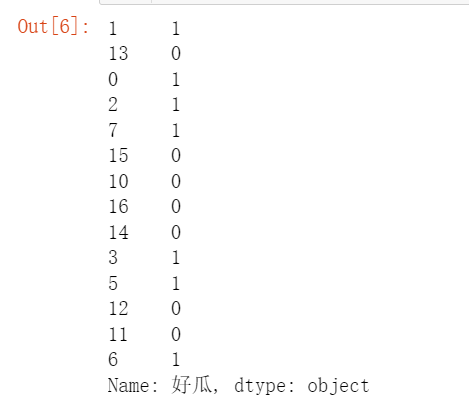
from sklearn.model_selection import train_test_split #将原始数据划分为数据集与测试集两个部分 from sklearn.naive_bayes import BernoulliNB X=data1.iloc[:,:-1] y=data1.iloc[:,-1] #X_train训练样本, X_test测试样本, y_train训练样本分类, y_test测试样本分类 #X样本数据分类集, y分类结果集, test_size=3测试样本数量,random_state=1 生成数据随机 X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=3,random_state=None)
4.
X_train
5.
X_test
6.
y_train
7.
y_test

8.
clf = BernoulliNB()
clf.fit(X,y)

9.
# 返回预测的精确性 clf.score(X_test, y_test)

10.
# 查看预测结果 clf.predict(X_test)

11.
#测试样本 ['青绿','蜷缩','浊响','清晰','凹陷','硬滑'] tt=['0','0','0','0','0','2']
12.
tt=pd.DataFrame(tt) test=tt.T
test

13.
# 查看预测结果 clf.predict(test)

三、朴素贝叶斯算法的应用场景
1.文本分类、垃圾文本过滤、情感判别
2.多分类实时预测
3.推荐系统



 浙公网安备 33010602011771号
浙公网安备 33010602011771号