卷积神经网络CNN的原理（二）－－－公式推导

　　卷积神经网络与普通神经网络的区别在于，卷积神经网络包含多个由卷积层和池化层构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元连接。在CNN的一个卷积层中，通常包含若干个特征平面(featureMap)，每个特征平面由一些矩形排列的的神经元组成，同一特征平面的神经元共享权值，这里共享的权值就是卷积核。卷积核一般以随机小数矩阵的形式初始化，在网络的训练过程中卷积核将学习得到合理的权值。共享权值（卷积核）带来的直接好处是减少网络各层之间的连接，同时又降低了过拟合的风险。子采样也叫做池化（pooling），通常有均值子采样（mean pooling）和最大值子采样（max pooling）两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度，减少了模型的参数。

　　神经网络的公式推导：

神经网络的每个单元如下：

 　　其对应的公式如下：

　　其中，该单元也可以被称作是Logistic回归模型。当将多个单元组合起来并具有分层结构时，就形成了神经网络模型。下图展示了一个具有一个隐含层的神经网络。

   　　　　 其对应的公式如下：

 

    多层的神经网络和这个比较类，神经网络可以扩展到有2,3,4,5，…个隐含层。

 神经网络的训练方法也同Logistic类似，不过由于其多层性，还需要利用链式求导法则对隐含层的节点进行求导，即梯度下降+链式求导法则，专业名称为反向传播。

　　卷积的公式：

卷积的概念，高等数学里面才接触到，大学没有好好学习的同学，是不是此处要泪奔了：

它的物理意义大概可以理解为：系统某一时刻的输出是由多个输入共同作用（叠加）的结果。放在图像分析里，f(x) 可以理解为原始像素点(source pixel)，所有的原始像素点叠加起来，就是原始图了。

h(T)可以称为作用点，所有作用点合起来我们称为卷积核（Convolution kernel）

　　微积分中卷积的表达式为：

 

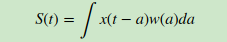
　　　　离散形式是：

 

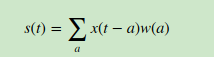
　这个式子如果用矩阵表示可以为：

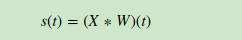
 　　其中星号表示卷积。

如果是二维的卷积，则表示式为：

 

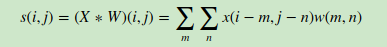
 　　在CNN中，虽然我们也是说卷积，但是我们的卷积公式和严格意义数学中的定义稍有不同,比如对于二维的卷积，定义为：

　　这个式子虽然从数学上讲不是严格意义上的卷积，但是大牛们都这么叫了，那么我们也跟着这么叫了。其中，我们叫W为我们的卷积核，而X则为我们的输入。如果X是一个二维输入的矩阵，而W也是一个二维的矩阵。但是如果X是多维张量，那么W也是一个多维的张量。

 今日格言：心伤也不是坏事，说明你曾经付出过 

献给正在为梦想付出的人

 参考文档：

１　https://zhuanlan.zhihu.com/p/25249694

2     https://www.zhihu.com/question/22298352

3      http://www.cnblogs.com/pinard/p/6483207.html