[1] mysql索引的数据结构比较: http://www.liuzk.com/410.html
[2]深入理解硬盘原理: https://blog.csdn.net/srs1995/article/details/107028790
[3]演示数据结构动画:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
mysql B+ 树
1、索引的分类
- B+树索引
- Hash索引
- 全文索引
2、各种查找树
2.1 二叉查找树

如图,我们为user表新建了一个二叉树查找树,注意,节点中同时保存了存储的键值和实际的数据data,对应到user表中,键值对应user表的id,数据对应id对应的行数据。
二叉查找树的特点
任何节点的左子节点的键值小于当前节点的键值任何节点的右子节点的键值大于当前节点的键值- 最顶端的节点,我们称之为根节点; 没有子节点的节点我们称之为叶子节点
查找数据的过程
例如,我们现在查找id=12 的数据,其过程为:
- 我们以根节点为当前节点,将key比较,12 > 10,那么当前节点变成当前节点的右子节点;
- 我们key再比较, 12> 13 ,那么当前节点移动到当前节点的左子节点;
- 我们key再比较,12 = 12 , 查找到数据,结束查找
由上面的过程,我们查找3次,查到到了数据
2.2 平衡二叉树
由2.1 的二叉树,我们的查询速度变快了,但是如果我们的二叉树变成如下结构:
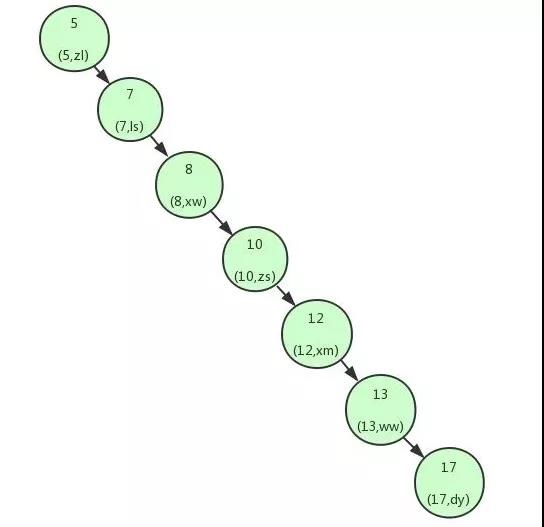
-
产生的问题:
我们再数据插入的时候,导致数据变成这样的结构,相当于链表了。当我们查找id=17 的数据时,我们必须要查找7次,相当于全表扫描。
-
产生的原因:
由于二叉树变得不平衡导致的,也就是高度太高,导致我们查询的效率不稳定。 -
解决办法:
我们再构建二叉树的时候,需要保证二叉树的平衡,也就是平衡二叉树。
平衡二叉树,又称为AVL树,在二叉树的特性上,每个节点的子数高度相差不能超过1
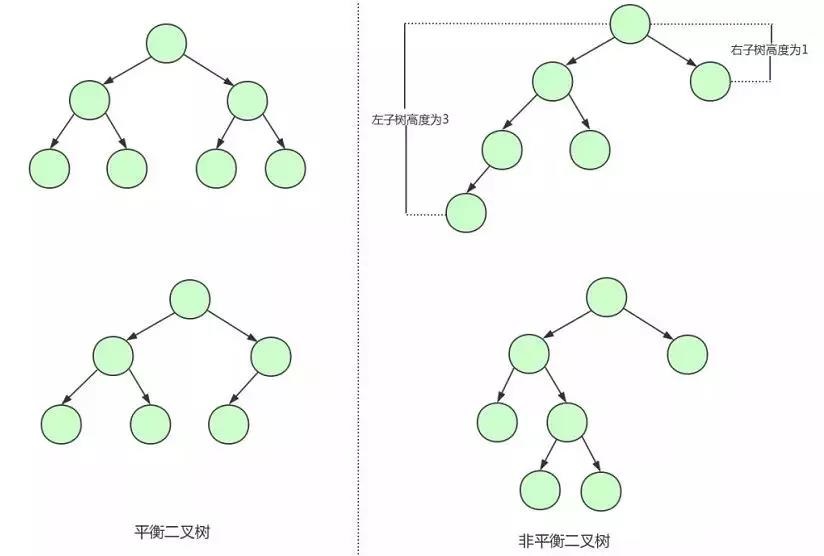
由图所示,最开始的那个就是一个平衡二叉树,为了保持二叉树的平衡,需要插入数据的时候进行相应的调整,具体方式:~~~~
- 结论:平衡二叉树[AVL]查询更加稳定,总体的查询效率比二叉树更高
2.3 B树
内存、机械硬盘、固态硬盘 - 专门研究一下
-
问题:
我们在平衡二叉树中,每个节点只保存了一个键值和数据,当我们保存海量的数据是,二叉树的高度就会非常高,而且磁盘的利用率也极低,访问磁盘的次数非常多,所以我们必须提高效率,一个节点保存多个键值。
-
解决:
B树(blacnce Tree)即平衡树,单节点上能保存多个键值和数据的平衡树。
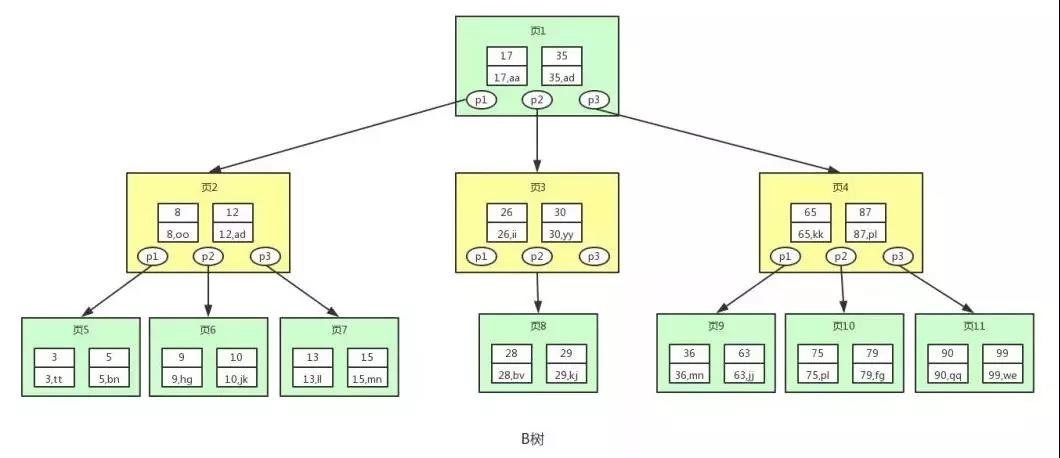
图中的每个节点,我们称之为页,mysql读取数据的最小单位就是页
从上图可以看出:
- B树的每个节点比平衡二叉树保存了更多的键值和数据;
- 每个节点拥有了更多的子节点;
子节点的个数一般被称之为阶数,以上图是一个3阶B数结构,这样B数的高度就相对变小。
基于上面的特性,B树查找数据访问磁盘的次数大大减小,查询效率较平衡二叉树提高很多。
查询数据的过程:
我们想要查询id=28的数据,那么过程如下:
- 我们从根节点开始查找,17< 28 < 35,我们可以判断到p2指针的第3页数据;
- 当前第3页节点, 26 < 28 <30,我们判断数据在当前节点的p2指针的第8页数据;
- 当前第8页节点, 28 =28 ,查询数据结束;
2.4 B+树
B+树是对B树的进一步优化

B树和B+树的区别
-
B+树的非叶子节点上不保存数据,仅仅保存键值;B树的每一个节点既保存键值又保存数据;
-
在数据库中页的大小是固定的,innDB中默认大小时16KB; -
B+ 树的阶数等于可保存键值的数量;如果我们B+ 树一个节点可以保存1000个键值,那么3阶B+树就可以保存: 1000x1000x1000=10亿的数据。一般根节点是常驻内存的,所以我们查找10亿数据,只需要访问两次磁盘! 真牛皮
-
-
B+树索引的所有数据保存在叶子节点,而且是按照顺序排列的;
- 由于B+树这样的特性,使得范围查找、分组查找、排序变得异常简单;B树中,数据非常分散无法快速得分组,排序等等。
-
B+树的键值保存页之间用双向链表连接的,叶子节点的数据之间用单向链表连接;
上图就是InnDB索引在磁盘保存真正的数据结构;
在MyISam中,有一点点不同B+树的叶子节点不存储数据,只保存数据的文件地址;
3、B+树索引的分类
3.1 聚集索引
以innDB作为存储引擎的表,表中的数据都会有一个主键,即使你不创建主键,系统也会帮你创建一个隐式的主键。
InnDB把数据存放在B+树中,而B+树的键值就是主键,在B+树的叶子节点中保存了表的所有数据。
这种以主键为B+树索引的键值而构建的B+树,我们称之为聚集索引。
3.2 非聚集索引
以非主键的列为B+树的键值构建的B+树,我们称之为非聚集索引。
3.3 聚集索引与非聚集索引之间的区别
非聚集索引的叶子节点不存储表中的数据,而是存储改列对应的主键,查找数据的时候,我们还需要在根据聚集索引的主键进行查找,这个根据聚集索引查找数据的过程我们称之为回表;
数据就是索引,索引就是数据
3.4 聚集索引查找数据
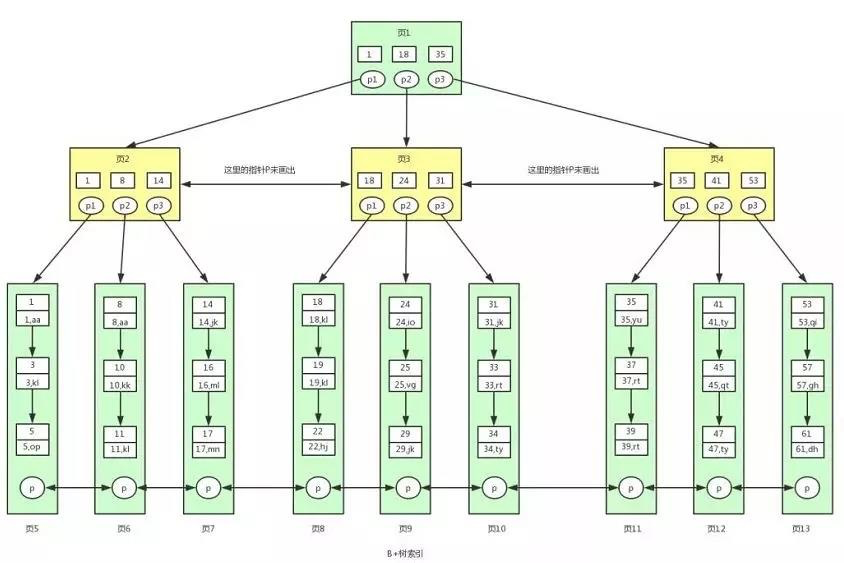
假设我们现在需要查询 id<=18 <40的用户数据:
select * from user where id >=18 and id < 40;
具体查找过程如下:
1、一般根节点是常驻内存中,也就是页1保存在内存中,直接读取;我们首先要找到id=18的页,根据p2然后定位到页3;
2、我们带着p2指针定位到页3,从磁盘中加载页3放入内存,然后进行查找,我们查找到了18,根据p1定位到了页8;
3、同样页8 不存在内存中,我们根据p1定位到了页8 ,加载到内存中;因为页中的数据是用链表进行连接的,而且键值是按照顺序排序的,用二分法定位数据18的数据。
因为数据页是连续保存数据的,我们根据范围查找连续遍历取到我们想要的数据,一直到id=22时,数据页没有了数据。
此时我们根据p直接去查找到第9页的数据。
4、再将第9页数据加载到内存中,并通过和页 8 中一样的方式进行数据的查找,直到将页 12 加载到内存中,发现 41 大于 40,此时不满足条件。那么查找到此终止
最终我们找到满足条件的所有数据,总共 12 条记录:
(18,kl), (19,kl), (22,hj), (24,io), (25,vg) , (29,jk), (31,jk) , (33,rt) , (34,ty) , (35,yu) , (37,rt) , (39,rt) 。
完整的查找过程:

3.5 非聚集索引查找数据
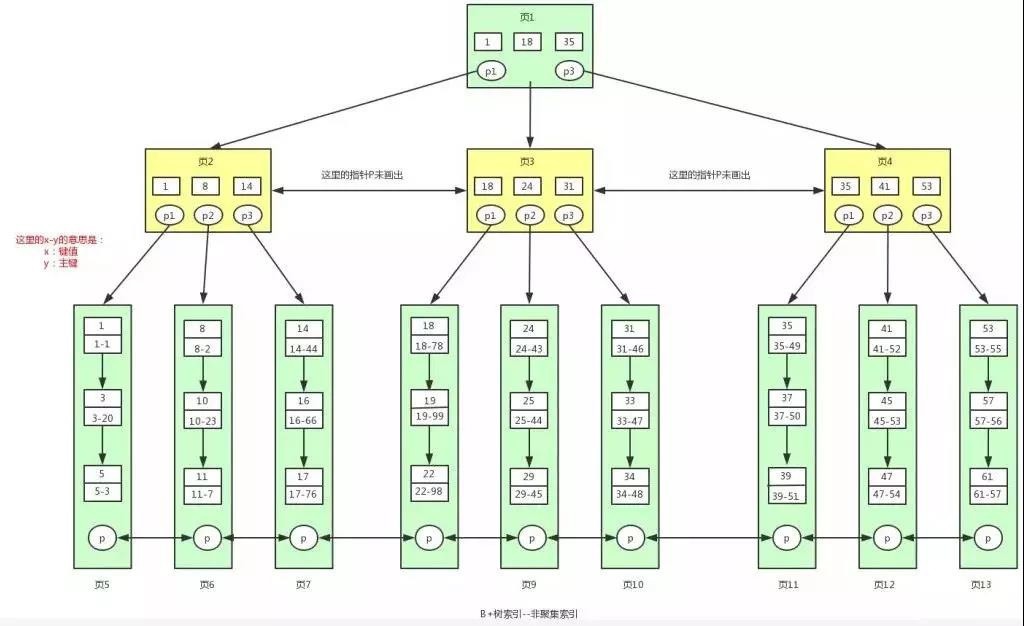
数据表为:
| id | name | luckynum |
|---|---|---|
| 1 | zs | 23 |
| 2 | ls | 7 |
在非聚集索引中,索引B+树的叶子节点不再保存数据了,保存键值和主键,对于叶子节点中的 x-y,比如 1-1。左边的 1 表示的是索引的键值,右边的 1 表示的是主键值。
select * from user where luckNum=33
具体的查找过程
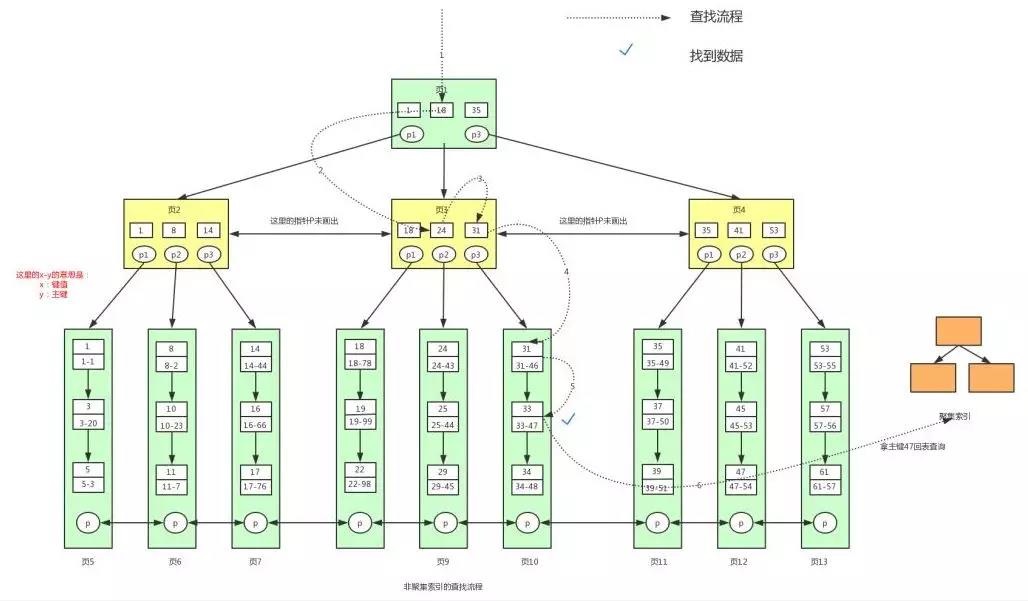
在 MyISAM 中,聚集索引和非聚集索引的叶子节点都会存储数据的文件地址。
总而言之,言而总之,数据就是索引,索引就是数据。
4、磁盘
4.1 硬盘的原理
大部分的存储设备信息都是保存在磁盘里面的,磁盘上被磁化的代表1,没有被磁化的代表0,用二进制来存储信息。
4.2 硬盘的组成

一般来说,硬盘都是由盘片、磁头、主轴、控制电机、数据转换器、接口、缓存等几个部分组成。
4.3 硬盘的工作原理
- 硬盘在逻辑上被划分为磁道、柱面以及扇区

- 盘面号: 扇区所在的刺头柱面好:磁道
访问磁盘的过程
确定磁盘地址(柱面好,磁头号,扇区号),内存地址(源/目):当需要从磁盘读取数据时,系统会将数据逻辑地址传给磁盘,磁盘的控制电路按照寻址逻辑将逻辑地址翻译成物理地址,确定数据在哪个磁道,哪个扇区
- 为了读取这个扇区的数据,需要将刺头放到这个扇区上方,为实现这一点:
- 必须找到柱面,即刺头需要移动到对应的磁道,这个时间叫寻道;
- 然后目标扇区旋转到磁头下,即磁盘旋转将扇区旋转到磁头下,这个耗费的时间叫做旋转时间
即一次访盘请求(读/写)完成过程由三个动作组成:
1)寻道(时间) :磁头移动定位到指定磁道
2)旋转延迟(时间):等待指定扇区从磁头下旋转经过
3)数据传输(时间):数据在磁盘与内存之间的实际传输
因此,磁盘读取一个扇区需要的时间:Ti/o = tseek + tla + n * twm
tseek 为寻道时间 tla为旋转时间 twm 为传输时间





