牛客题单_动态规划课程状压dp例题
牛客题单_动态规划课程状压dp例题
NC15832 Most Powerful
大意：
现在有n个石头，每个石头碰撞都会产生能量，现在给出一个矩阵A,\(a_{i,j}\)代表石头i和石头j碰撞后且石头j消失时释放的能量，问将n个石头进行n-1次碰撞，产生的能量最多是多少
思路：
\(dp[i]\)代表i的二进制位上为1的石头已经消失时释放的能量，这样对于每个已经消失的石头，都可以枚举没有消失的石头来转移，最后枚举最后留下哪个石头即可
#include <bits/stdc++.h>
using namespace std;
const int N = 20 + 5;
typedef long long LL;
int n, a[N][N], dp[1<<12];
int main() {
while (scanf("%d", &n) && n != 0) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> a[i][j];
}
}
memset(dp, 0, sizeof dp);
int num = (1 << n) - 1;
for (int i = 0; i <= num; i++) {
for (int j = 0; j < n; j++) {
if (i & (1 << j)) {
for (int k = 0; k < n; k++) {
if (!(i & (1 << k))) {
dp[i] = max(dp[i], dp[i - (1 << j)] + a[k][j]);
}
}
}
}
}
int res = 0;
for (int i = 0; i < n; i++) {
res = max(res, dp[num - (1 << i)]);
}
cout << res << endl;
}
return 0;
}
NC16122 郊区春游
大意：
在铁子的城市里有n个郊区和m条无向道路，第i条道路连接郊区Ai和Bi，路费是Ci。经过铁子和顺溜的提议，他们决定去其中的R个郊区玩耍（不考虑玩耍的顺序），但是由于他们的班费紧张，所以需要找到一条旅游路线使得他们的花费最少，假设他们制定的旅游路线为V1, V2 ,V3 ... VR，那么他们的总花费为从V1到V2的花费加上V2到V3的花费依次类推，注意从铁子班上到V1的花费和从VR到铁子班上的花费是不需要考虑的
思路：
首先Floyd计算两个点之间的最短路，然后枚举状态，用当前的状态更新没有到过的点的状态
\(dp[i][j]\)代表已经走过的点的状态为i，当前停在j点
#include <bits/stdc++.h>
using namespace std;
const int N = 2e2 + 5;
typedef long long LL;
int n, m, r;
int mp[N][N], add[20], dp[1 << 16][20];
void floyd() {
for (int k = 0; k < n; ++k) // 枚举中间点
for (int i = 0; i < n; ++i) // 枚举起点
for (int j = 0; j < n; ++j) // 枚举终点
mp[i][j] = min(mp[i][j], mp[i][k] + mp[k][j]); // 更新i到j的距离
}
int main() {
cin >> n >> m >> r;
memset(mp, 0x3f, sizeof mp);
memset(dp, 0x3f, sizeof dp);
for (int i = 0; i < n; i++) mp[i][i] = 0;
for (int i = 0; i < r; i++) cin >> add[i],add[i]--;
for (int i = 0; i < m; i++) {
int x, y, w;
cin >> x >> y >> w;
x--, y--;
if (mp[x][y] > w) {
mp[x][y] = w;
mp[y][x] = w;
}
}
floyd();
int num = (1 << r) - 1;
for (int i = 0; i < r; i++) dp[1 << i][i] = 0;
for (int i = 0; i <= num; i++) {
for (int j = 0; j < r; j++) {
if (i & (1 << j)) {
for (int k = 0; k < r; k++) {
if (!(i & (1 << k)))
dp[i+(1<<k)][k] = min(dp[i+(1<<k)][k], dp[i][j] + mp[add[j]][add[k]]);
}
}
}
}
int res = 0x3f3f3f3f;
for (int i = 0; i < r; i++) {
res = min(res, dp[num][i]);
}
cout << res << endl;
return 0;
}
NC16544 简单环
大意：
给定一张n个点m条边的无向图，求出图中所有简单环的数量。(简单环：简单环又称简单回路，图的顶点序列中，除了第一个顶点和最后一个顶点相同外，其余顶点不重复出现的回路叫简单回路。或者说，若通路或回路不重复地包含相同的边，则它是简单的)
思路：
设\(dp[status][i]\)表示当前枚举的链为集合status（注意当前是一条链，枚举的子集不能当成环）
以i这个点为结束点，以status的第一个开始点为起始点的方案数，转移的时候枚举在子集中的点j，不在status子集中的点k，看点k是否可以加入这条链，\(dp[status|(1<<k)][k]+=dp[status][j]\)，然后再看k是否可以和status的起点建边，如果可以，这就是一个合法的简单环方案，加入答案。
需要注意的是，因为dp表示的是以status的第一个点作为起点的链的数量，所以枚举k的时候，要从第一个点以后的点开始枚举，否则会导致重复
另外，在统计答案的时候，仍然要将答案除以2，因为对于每个环，都统计了顺时针和逆时针两种情况，因为这里取模了，所以要用2
的逆元
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n, m, k, mp[30][30];
const LL mod = 998244353;
LL dp[1 << 21][21], sum[30], res[30];
int main() {
cin >> n >> m >> k;
for (int i = 0; i < m; i++) {
int x, y;
cin >> x >> y;
mp[x][y] = mp[y][x] = 1;
}
int num = (1 << n) - 1;
for (int i = 1; i <= n; i++) dp[1 << (i - 1)][i] = 1;
for (int i = 1; i <= num; i++) {
int s = -1;
for (int j = 1; j <= n; j++) {
if (i & (1 << (j - 1))) {
s = j;
break;
}
}
for (int j = 1; j <= n; j++) {
if (dp[i][j]) {
for (int k = s + 1; k <= n; k++) {
if (!(i & (1 << (k - 1))) && mp[j][k]) {
dp[i + (1 << (k - 1))][k] =
(dp[i + (1 << (k - 1))][k] + dp[i][j]) % mod;
}
}
if (mp[j][s]) {
if (__builtin_popcount(i) < 3) continue;
res[__builtin_popcount(i) % k] =
(res[__builtin_popcount(i) % k] + dp[i][j]) % mod;
}
}
}
}
for (int i = 0; i < k; i++) {
cout << (res[i] * ((LL)(mod + 1) / 2) % mod) % mod << endl;
}
return 0;
}
NC16886 炮兵阵地
大意： 司令部的将军们打算在N * M的网格地图上部署他们的炮兵部队。一个N * M的地图由N行M列组成，地图的每一格可能是山地（用”H” 表示），也可能是平原（用”P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：
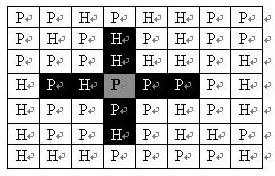
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。输出最多能摆放的炮兵部队的数量。N≤100,M≤10
思路：
\(dp[now][i][j]\)表示当前行的状态为j，上一行的状态为i的答案，那么每次转移都可以利用上上行与上一行的状态的答案来转移
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 10, M = 1 << 10;
int n, m;
int g[1010];
int f[2][M][M];
vector<int> state;
int cnt[M];
bool check(int state) {
for (int i = 0; i < m; i ++ )
if ((state >> i & 1) && ((state >> i + 1 & 1) || (state >> i + 2 & 1)))
return false;
return true;
}
int count(int state) {
int res = 0;
for (int i = 0; i < m; i ++ )
if (state >> i & 1)
res ++ ;
return res;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < m; j ++ ) {
char c;
cin >> c;
g[i] += (c == 'H') << j;
}
for (int i = 0; i < 1 << m; i ++ )
if (check(i)) {
state.push_back(i);
cnt[i] = count(i);
}
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < state.size(); j ++ )
for (int k = 0; k < state.size(); k ++ )
for (int u = 0; u < state.size(); u ++ ) {
int a = state[j], b = state[k], c = state[u];
if (a & b | a & c | b & c) continue;
if (g[i] & b | g[i - 1] & a) continue;
f[i & 1][j][k] = max(f[i & 1][j][k], f[i - 1 & 1][u][j] + cnt[b]);
}
int res = 0;
for (int i = 0; i < state.size(); i ++ )
for (int j = 0; j < state.size(); j ++ )
res = max(res, f[n & 1][i][j]);
cout << res << endl;
return 0;
}
NC20240 [SCOI2005]互不侵犯KING
在N×N的棋盘里面放K个国王，使他们互不攻击，共有多少种摆放方案。
国王能攻击到它上下左右，以及左上 左下右上右下八个方向上附近的各一个格子，共8个格子。
和上个题类似的模板题
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 12, M = 1 << 10, K = 110;
int n, m;
vector<int> state;
int cnt[M];
vector<int> head[M];
LL f[N][K][M];
// 计算每种情况是否合法
bool check(int state) {
for (int i = 0; i < n; i ++ )
if ((state >> i & 1) && (state >> i + 1 & 1))
return false;
return true;
}
// 计算每种情况内的1
int count(int state) {
int res = 0;
for (int i = 0; i < n; i ++ ) res += state >> i & 1;
return res;
}
int main() {
cin >> n >> m;
// 记录所有合法的情况，同时计算出每种合法情况的1数目
for (int i = 0; i < 1 << n; i ++ )
if (check(i)) {
state.push_back(i);
cnt[i] = count(i);
}
// 计算哪两种合法情况间能够互相匹配
for (int i = 0; i < state.size(); i ++ )
for (int j = 0; j < state.size(); j ++ ) {
int a = state[i], b = state[j];
if ((a & b) == 0 && check(a | b))
head[i].push_back(j);
}
// 状态转移：f[i][j][a]:到第i行，使用了j个，第i行填充a
f[0][0][0] = 1; // 本题入口与蒙德里安的梦想不同是因为本题的第一列可以填东西，而蒙德里安的梦想第一列不可以填东西
for (int i = 1; i <= n + 1; i ++ )
for (int j = 0; j <= m; j ++ )
for (int a = 0; a < state.size(); a ++ )
for (int b : head[a]) { // 第i-1行填充b
int c = cnt[state[a]];
if (j >= c)
f[i][j][a] += f[i - 1][j - c][b];
}
cout << f[n + 1][m][0] << endl; // 输出第n+1行，使用了m个，第n+1行填充0的情况
return 0;
}
NC51189 Mondriaan's Dream
大意： 求把N * M的棋盘分割成若干个1 * 2的的长方形，有多少种方案。
例如当N=2，M=4时，共有5种方案。当N=2，M=3时，共有3种方案。
如下图所示：
1≤N,M≤11
思路： 我们可以规定砖头的竖放的上部分为1，砖头的横放或者是竖放的下部分为0。这样的话，单排的情况就本题列数最多的情况，最小状压出来的就是000000000000000000000000000000000，而最大的是111111111111111111111111111111111。而仔细想一下就会发现最后一行因为不能为竖放的上部分，也就是不能为1，那么最后一行的情况必定全都是0。仔细考虑就可以知道全部的方案是取决于横的方块的方案，一旦横的方块确定后竖的方块也就确定了。使用f [i] [j]表示前i-1列填完，第i列为j的情况，那么能够合法填充的j和k满足，j&k==0且j|k之间连续的1为偶数。那么考虑dp的转移方程为:f [i] [j]+= f [i-1] [k] (k是和j能够匹配的合法方案)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, m;
int const N = 1e4 + 10;
LL f[20][N];
int st[N];
vector<int> state[N];
int main() {
while (cin >> n >> m && n && m) {
// 初始化
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 0; i < 1 << n; ++i) state[i].clear();
// 预处理st
for (int i = 0; i < 1 << n; i ++ ) {
int cnt = 0;
st[i] = true;
for (int j = 0; j < n; j ++ )
if (i >> j & 1) {
if (cnt & 1) st[i] = false;
cnt = 0;
}
else cnt ++ ;
if (cnt & 1) st[i] = false;
}
// 预处理state
for (int i = 0; i < 1 << n; ++i) {
for (int j = 0; j < 1 << n; ++j) {
if ((i & j) == 0 && st[i | j]) state[i].push_back(j);
}
}
// dp转移
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < 1 << n; ++j) {
for (int k = 0; k < state[j].size(); ++k) { // 获得所有的合法方案
f[i][j] += f[i - 1][state[j][k]];
}
}
}
printf("%lld\n", f[m][0]);
}
return 0;
}
