Kuangbin 博弈专题
Kuangbin 博弈专题
- Kuangbin 博弈专题
- HDU 1079 Calendar Game
- HDU 1525 Euclid's Game
- HDU 1564 Play a game
- HDU 1846 Brave Game
- HDU 1847 Good Luck in CET-4 Everybody!
- HDU 2516 取石子游戏
- HDU 2897 邂逅明下
- HDU 3032 Nim or not Nim?
- HDU 3389 Game
- HDU 3537 Daizhenyang's Coin
- HDU 3544 Alice's Game
- HDU 3863 No Gambling
- HDU 3951 Coin Game
- HDU 2188 悼念512汶川大地震遇难同胞――选拔志愿者
- HDU 2149 Public Sale
- HDU 1850 Being a Good Boy in Spring Festival
- HDU 2176 取(m堆)石子游戏
- HDU 1527 取石子游戏
- HDU 2177 取(2堆)石子游戏
- HDU 1517 A Multiplication Game
- HDU 2486 A simple stone game
- HDU 4315 Climbing the Hill
- HDU 1538 A Puzzle for Pirates
- HDU 3404 Switch lights
HDU 1079 Calendar Game
大意：
A和B两个人从一个日期开始，A先手，可以将这个日期变为下一天，或者是下个月中相同的天，有效的日期为1900年1月1日至2001年11月4日，无法取的人输，现在给出开始日期，问先手输赢
思路：
sg函数简单题，不过写日期写了好久...
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int t;
int f[150][15][35];
bool is_leap(int y) {
if (y % 4 == 0 && y % 100 != 0) return 1;
if (y % 400 == 0) return 1;
return 0;
}
bool check(int y, int m, int d) {
if (y > 2001) return 0;
if (y == 2001 && m > 11) return 0;
if (y == 2001 && m == 11 && d > 4) return 0;
if(m == 4 || m == 6 || m == 9 || m == 11){
if (d == 31) return 0;
}
if(m==2&&!is_leap(y)){
if (d == 29) return 0;
}
return 1;
}
int sg(int y, int m, int d) {
//cout << y << ' ' << m << ' ' << d << endl;
if (f[y - 1900][m][d] != -1) return f[y - 1900][m][d];
int ny, nm, nd;
//下一天
if (d == 31) {
nd = 1;
if (m == 12) {
nm = 1, ny = y + 1;
} else
ny = y, nm = m + 1;
} else if (d == 30) {
ny = y;
if (m == 4 || m == 6 || m == 9 || m == 11) {
nm = m + 1, nd = 1;
} else
nm = m, nd = d+1;
} else if (d == 29 && m == 2) {
ny = y, nm = 3, nd = 1;
}
else if(d==28&&m==2&&is_leap(y)){
ny = y, nm = 2, nd = 29;
}
else if(d==28&&m==2){
ny = y, nm = 3, nd = 1;
}
else{
ny = y, nm = m, nd = d + 1;
}
if(check(ny,nm,nd)){
if (sg(ny, nm, nd)==0) return f[y - 1900][m][d] = 1;
}
//下一月
if(m==12){
ny = y + 1, nm = 1, nd = 1;
}
else
ny = y, nm = m + 1, nd = d;
if(check(ny,nm,nd)){
if (sg(ny, nm, nd)==0) return f[y - 1900][m][d] = 1;
}
return f[y - 1900][m][d] = 0;
}
int main() {
cin >> t;
memset(f, -1, sizeof f);
f[2001 - 1900][11][4] = 0;
while (t--) {
int y, m, d;
cin >> y >> m >> d;
if (sg(y, m, d))
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}
HDU 1525 Euclid's Game
大意：
有n和m两个数，每次可以从较大的那个数里取出较小的那个数的倍数，直到一个数变为0，不能取的人输，问先手是否必胜
思路：
非常玄妙，我愿称之为欧几里得博弈模型（doge)
dfs，假设当前两个数为a、b且a>=b，如果当前b==0，则必败，如果当前a % b ==0,则必胜，因为直接把a减到0即可
如果a大于b的两倍，那么也是必胜，因为此时：
如果b,a%b是必败态，先手将a,b变成b,a%b,那么先手肯定赢。
如果b,a%b是必胜态，先手将a,b变成b,a%b+b,那么对手只有将这两个数变成a%b,b,所以先手获胜。
而a在2b到b之间，那么只好直接dfs往下找，找到之后返回
#include <bits/stdc++.h>
using namespace std;
int c, a, b;
bool dfs(int a, int b) {
if (a < b) swap(a, b);
if (b == 0) return 0;
if (dfs(b, a % b) == 0 || a > b * 2)
return 1;
else
return 0;
}
int main() {
while (scanf("%d %d", &a, &b)&&(a+b!=0)) {
if (b > a) swap(a, b);
if (dfs(a, b))
printf("Stan wins\n");
else
printf("Ollie wins\n");
}
return 0;
}
HDU 1564 Play a game
大意：
一个nxn的棋盘，一个石头放在角落，轮流将这个石头移动到没有经过的位置，直到不能移动为止
思路：
猜结论+推理：一共有(n+1)^2个点，除去第一个点以外，如果有奇数个，那么一定是先手赢，因为走满了之后后手就走不了了，反之就是后手赢
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5;
typedef long long LL;
LL n;
int main(){
while(scanf("%lld",&n)&&n!=0){
n++;
if(n*n%2==0){
cout << "ailyanlu" << endl;
}
else
cout << "8600" << endl;
}
return 0;
}
HDU 1846 Brave Game
巴什博弈裸题
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, m, t;
cin >> t;
while (t--) {
cin >> n >> m;
if (n % (m + 1) == 0)
cout << "second" << endl;
else
cout << "first" << endl;
}
return 0;
}
HDU 1847 Good Luck in CET-4 Everybody!
给出n个石子，每次可以从中取出2的幂次，不能取的输
找规律结论：对3取模为0则先手必败（类似luogu p4018Roy&October之取石子，对6取模），因为3的倍数都不是2的幂次
#include <bits/stdc++.h>
using namespace std;
int n;
int main() {
while (scanf("%d", &n) != EOF)
n % 3 == 0 ? cout << "Cici" << endl : cout << "Kiki" << endl;
}
HDU 2516 取石子游戏
斐波那契博弈裸题(“Zeckendorf定理”（齐肯多夫定理）：任何正整数可以表示为若干个不连续的Fibonacci数之和。)
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
int f[N];
void Init() {
f[0] = f[1] = 1;
for(int i=2;i<N;i++)
f[i] = f[i-1] + f[i-2];
}
int main() {
Init();
int n;
while(cin>>n) {
if(n == 0) break;
bool flag = 0;
for(int i=0;i<N;i++) {
if(f[i] == n) {
flag = 1;
break;
}
}
if(flag) puts("Second win");
else puts("First win");
}
return 0;
}
HDU 2897 邂逅明下
大意：
每行有三个数字n，p，q，表示一堆硬币一共有n枚，从这个硬币堆里取硬币，一次最少取p枚，最多q枚，如果剩下少于p枚就要一次取完。两人轮流取，直到堆里的硬币取完，最后一次取硬币的算输。对于每一行的三个数字，给出先取的人是否有必胜策略，如果有回答WIN，否则回答LOST。
思路：
类似巴什博弈，用和巴什博弈差不多的思路去推就行
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n, p, q;
int main() {
while (cin >> n >> p >> q)
if (n <= p) {
cout << "LOST" << endl;
} else {
n -= p;
if ((n-1) % (p + q) < q) {
cout << "WIN" << endl;
} else {
cout << "LOST" << endl;
}
}
return 0;
}
HDU 3032 Nim or not Nim?
大意：
给出n堆石头，每次可以从一堆里面取出任意（至少是1）个石头，或者将一堆石头分成两堆，不能操作的人输
思路：
n和ai都很大，没法直接用sg去搜，但是可以打表：
int sg(int x) {
if (f[x] != -1) return f[x];
unordered_set<int> s;
for (int i = 1; i <= x; i++) {
s.insert(sg(x-i)); //从中拿出任意一个
}
for (int i = 1; i < x; i++) {
s.insert(sg(i) ^ sg(x - i)); //分成两份，此时sg需要用异或求（因为是两个堆）
}
for (int i = 0;; i++) {
if (!s.count(i)) return f[x] = i;
}
}
打表发现当n%4 == 3时，sg=n+1，当n % 4== 0 时，sg=n-1
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5;
typedef long long LL;
int f[N];
int sg(int x) {
if (f[x] != -1) return f[x];
unordered_set<int> s;
for (int i = 1; i <= x; i++) {
s.insert(sg(x-i)); //从中拿出任意一个
}
for (int i = 1; i < x; i++) {
s.insert(sg(i) ^ sg(x - i)); //分成两份，此时sg需要用异或求（因为是两个堆）
}
for (int i = 0;; i++) {
if (!s.count(i)) return f[x] = i;
}
}
int sg2(int x){
if (x % 4 == 3) return x + 1;
if (x % 4 == 0) return x - 1;
else return x;
}
int main() {
/*
memset(f, -1, sizeof f);
for (int i = 0; i <= 1000;i++){
cout <<i<<' '<< sg(i) << endl;
}
*/
int t;
cin>>t;
while(t--){
int n;
cin >> n;
int res = 0;
while(n--){
int x;
cin>>x;
res ^= sg2(x);
}
if (res) cout << "Alice" << endl;
else cout << "Bob" << endl;
}
return 0;
}
HDU 3389 Game
大意：
给出n个位置，每个位置上有ai个石子，设当前点为A，每次可以选择一个点B，满足B<A && (A+B)%2=1 && (A+B)%3=0，然后将A上的任意个点转移到B，不能转移则输
思路：
阶梯博弈的思路，寻找移动奇数步的位置，然后将其异或即可,找规律发现模6为0 2 5的位置移动步数为奇数
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int t, cases = 0;
int main() {
cin >> t;
while (t--) {
int n;
cases++;
cin >> n;
int res = 0;
for (int i = 1; i <= n; i++) {
int x;
cin>>x;
if (i % 6 == 0 || i % 6 == 2 || i % 6 == 5) res ^= x;
}
if (res) cout << "Case "<<cases<<": Alice" << endl;
else cout << "Case "<<cases<<": Bob" << endl;
}
return 0;
}
HDU 3537 Daizhenyang's Coin
翻硬币游戏的第6种模型
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n;
int sg(int x) {
int num = 0;
int t=2* x;
while (t) {
if (t & 1) num++;
t /= 2;
}
if (num & 1) return 2 * x;
else return 2 * x + 1;
}
int main() {
while (cin >> n) {
set<int> s;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
s.insert(x);
}
int res = 0;
for (auto i : s) {
res ^= sg(i);
}
if (res) cout << "No" << endl;
else cout << "Yes" << endl;
}
return 0;
}
HDU 3544 Alice's Game
大意：
给出一些巧克力，Alice可以每次选择一个巧克力，将其竖着切开，Bob每次选择一个将其横着切开，但是得到的尺寸必须是整数，不能切的输
思路：
因为两个人的选择方法不同，所以是一个不平等博弈
如果对于一个n * n的块,先切的人,就是给后切的人多了一次的切的数目，所以为了让后面的人少切，同时让自己多切，那么就从中间切开最优（因为如果不从中间切的话，后手可以从切下来的那两个中较小的那个切，这样先手下次切的时候可选择的余地就变小了）
所以两个人都是沿着中间切，那么算一下每个巧克力这么切下去最后是多少即可
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
#define int LL
int t;
signed main(){
cin>>t;
int cases=0;
while(t--){
cases++;
int n,a=0,b=0;
cin >> n;
while(n--){
int x,y;
cin>>x>>y;
while(x>1&&y>1){
x>>=1,y>>=1;
}
if(x>1)a+=x-1;
if(y>1) b+=y-1;
}
if(a>b)printf("Case %d: Alice\n",cases);
else printf("Case %d: Bob\n",cases);
}
return 0;
}
HDU 3863 No Gambling
给出一个尺寸为n的对称棋盘，先手走蓝色点，后手走红色，先手目标是连一条从左到右的线，后手是从上到下，如图b就是先手获胜
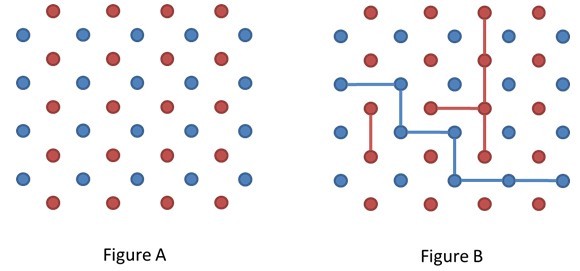
现在给出棋盘大小，问先手还是后手获胜
结论：对称图的游戏，先手必胜。但是没有找到严格的证明，网上一个帮助理解的思路是：画一下会发现，是先手必胜的，如果我们考虑后手一直都在堵先手的路，因为先手会比后手多走一步，所以说先手到达最右边是没法堵的，因为游戏已经结束了.
#include<bits/stdc++.h>
using namespace std;
int n;
int main(){
while(scanf("%d",&n)&&n!=-1){
cout << "I bet on Oregon Maple~" << endl;
}
return 0;
}
HDU 3951 Coin Game
大意：
给出n个硬币排成环形，每次可以取1到k个连续的硬币，不能取的人输
思路：
当k为1时，根据奇偶来判断
当k大于等于2时，先手取过一次之后，环形变成了一条连续的链，此时后手可以从中间取一个或者两个，使得剩下的硬币为对称的两段，然后先手怎么取我就怎么取即可，那么后手必赢，注意n小于等于k的特殊情况
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n, k;
int main() {
int t, cases = 0;
cin >> t;
while (t--) {
cin >> n >> k;
cases++;
if (k == 1) {
if (n % 2 == 0)
printf("Case %d: second\n", cases);
else
printf("Case %d: first\n", cases);
} else {
if (n <= k)
printf("Case %d: first\n", cases);
else
printf("Case %d: second\n", cases);
}
}
return 0;
}
HDU 2188 悼念512汶川大地震遇难同胞――选拔志愿者
巴什博弈裸题
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, m, t;
cin >> t;
while (t--) {
cin >> n >> m;
if (n % (m + 1) == 0)
cout << "Rabbit" << endl;
else
cout << "Grass" << endl;
}
return 0;
}
HDU 2149 Public Sale
大意：
刚开始底价为0，两个人轮流开始加价，不过每次加价的幅度要在1～N之间，当价格大于或等于田地的成本价 M 时，主办方就把这块田地卖给这次叫价的人。问先手第一次报价时，怎样报价才能必胜，如果能，输出第一次报价的全部策略，否则输出none
思路：
还是巴什博弈，必败的时候输出none，否则看怎么才能让对方必败即可
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n, m;
int main() {
while (scanf("%d%d", &m, &n) != EOF) {
if (m <= n) {
for (int i = m; i <= n; i++) {
if (i == m) cout << i;
else cout << ' ' << i;
}
cout << endl;
}
else{
if(m%(n+1)) cout << m % (n + 1) << endl;
else cout << "none" << endl;
}
}
return 0;
}
HDU 1850 Being a Good Boy in Spring Festival
大意：
有n堆石子，每次可以从任意一堆中取出任意个石子，问先手如果获胜，第一轮有多少种不同的取法
思路：
就是问NIM游戏第一步应该怎么走，这就要深刻理解NIM游戏sg的含义，当sg的异或和不等于0时，对于每一堆的sg，如果有取法，那么只有一种使整体的sg为0的取法，所以只需要扫一遍即可
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n, a[N];
int main() {
while (scanf("%d", &n) && n != 0) {
int sg = 0;
for (int i = 0; i < n; i++) {
cin >> a[i];
sg ^= a[i];
}
if (sg == 0)
cout << 0 << endl;
else {
int num = 0;
for (int i = 0; i < n; i++) {
if ((sg ^a[i])<=a[i]) num++;
}
cout << num << endl;
}
}
return 0;
}
HDU 2176 取(m堆)石子游戏
和上一题一样，不过是输出所有的方案,注意：sg^a[i] 是这堆石子应该剩下多少
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int m, a[N];
int main() {
while (scanf("%d", &m) && m != 0) {
int sg = 0;
for (int i = 0; i < m; i++) {
cin >> a[i];
sg ^= a[i];
}
if (sg == 0)
cout << "No" << endl;
else {
cout << "Yes" << endl;
for (int i = 0; i < m; i++) {
if ((sg ^ a[i]) <= a[i]) {
cout << a[i] << ' ' << (sg ^ a[i]) << endl;
}
}
}
}
return 0;
}
HDU 1527 取石子游戏
威佐夫博弈裸题
#include <bits/stdc++.h>
using namespace std;
int main() {
int n1, n2, temp;
while (cin >> n1 >> n2) {
if (n1 > n2) swap(n1, n2);
temp = floor((n2 - n1) * (1 + sqrt(5.0)) / 2.0);
if (temp == n1)
cout << "0" << endl;
else
cout << "1" << endl;
}
return 0;
}
HDU 2177 取(2堆)石子游戏
大意：
威佐夫博弈，要求输出第一步拿的方式
思路：
可以首先将必败局面打表记录下来，然后输出相应的局面
打表需要用到的两个性质：
必败局面中，a和b的差值是递增的，分别是0,1,2,3,4,5,6,7......n
局势的第一个值是未在前面出现过的最小的自然数。
例如：
第一种（0，0）
第二种（1，2）
第三种（3，5）
第四种 (4 ，7）
第五种（6，10）
第六种 (8，13）
第七种 (9 ， 15）
第八种 (11 ，18）
所以枚举差值，然后记录a和b即可，输出局面的时候，如果从两堆里面都拿，那么两个数的差值是不变的，所以直接看差值对应的a是否小于输入的n即可，如果只拿一堆，那么就看n和m分别做b，然后对应的a即可，最多只有三种情况
#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 5;
typedef long long LL;
int n, m, a[N/2], b[N/2];
bool vis[N];
double k = (1 + sqrt(5.0)) / 2.0;
int mp[N];
int main() {
int cnt = 0;
for (int i = 0; i <= 1e6; i++) {
if (!vis[i]) {
a[cnt] = i;
b[cnt] = i + cnt;
vis[i] = vis[i + cnt] = 1;
mp[i + cnt] = i;
cnt++;
}
}
while (scanf("%d%d", &n, &m) && (n + m != 0)) {
if (n > m) swap(n, m);
int temp = floor((m - n) * (1 + sqrt(5.0)) / 2.0);
if (temp == n)
cout << "0" << endl;
else {
cout << "1" << endl;
int sub = m - n;
if (a[sub] < n) {
cout << a[sub] << ' ' << b[sub] << endl;
}
if (mp[m]) {
if (mp[m] < n) cout << mp[m] << ' ' << m << endl;
}
if (mp[n]) {
if (n != m) cout << mp[n] << ' ' << n << endl;
}
}
}
return 0;
}
HDU 1517 A Multiplication Game
大意：
从1开始，两个人可以将当前的数乘上2到9之间的任意一个数，首先得到大于等于n的数的人赢
思路：
有点类似巴什博弈，首先将n一直除以18，然后得到一个数m，如果这个数小于等于9，那么先手可以第一次的时候将1乘到m，然后不管后手乘数k是几，先手都可以乘18/k，这样就可以在先手的时候超过n，注意需要用double
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int main() {
double n;
while (scanf("%lf", &n) != EOF) {
while (n > 18) n /= 18;
if (n > 9) cout << "Ollie wins." << endl;
else cout << "Stan wins." << endl;
}
return 0;
}
HDU 2486 A simple stone game
有n个石子，两个游戏者轮流操作，第一个操作的人最多能拿走n-1个石子，以后，每个游戏者最多能拿走前一个游戏者拿走数目的k倍，如果先手必败输出lose，否则输出必胜的情况下第一步拿走的石子数。
这就是K倍动态减法游戏，可以参考《曹钦翔从“k倍动态减法游戏”出发探究一类组合游戏问题》的论文。
首先k=1的时候，必败态是2 ^ i, 因为我们把数按二进制分解后，拿掉二进制的最后一个1，那么对方必然不能拿走倒数第二位的1，因为他不能拿的比你多。你只要按照这个策略对方一直都不可能拿完，而且一定会生成新的低位的1。所以你就会赢。而当分解的二进制中只有一个1时，因为第一次先手不能全部取完，所以后手一定有办法取到最后一个1，所以必败！
k=2的时候，即为斐波那契博弈，必败态是斐波那契数列，这里用到一个斐波那契数列的性质，即任何数都可以表示成若干个“互不相邻的”斐波那契数的和，而不相邻的斐波那契数所差的倍数都是大于2的，那么我们就可以类比K=1的情况，把N按这种“斐波那契数列”的数制分解，每次仍然是取走最低位的1，由于后手无法取走高两位之上的1而前边的不相邻有保证了不会有连续的1出现，所以接下来就和K=1的时候一样了，每次取走最低位的1直到结束。
k>2的时候,犹如Fibonacci博弈，我们首先要求一个数列，将n分解成数列中一些项的和，然后就可以按Fibonacci博弈的解决方法来完成，也可以按二进制的方法来理解，每次取掉最后一个1 还是符合上面的条件。
我们用a数组表示要被求的数列，b数组中的b[i]保存 a[0...i] 组合能够构造的最大数字。这儿有点难理解，所谓构造就是指n分解为Fib数相加的逆过程。举例说明，当k = 2 时，a[N]={1, 2, 3, 5, 8, 13, 21, 33....} （Fibonacci数组）；那么b[3] 即 1、2、 3 能够构造的最大数字，答案是4，有点匪夷所思？或许你会问为什么不是5、6或者其它的什么，其实是这样的 ，4 能分解成 1+3 是没有争议的，但5能分解成2+3吗? 不能，因为5本身也是Fibonacci数；6虽然能分解，但不是分解成1+2+3，而是分解成1+5。
经过上述，我们知道b[i] 是 a[0...i] 能够构造出的最大数字，那么a[i +1] = b[i]+1；因为a数组（Fib数组）所存的数字都是不可构造的（取到它本身就是必败态），显然a[0...i]构造的最大数字 + 1 即为下一个不可构造的数字了(a[i + 1])。
然后关于b[i]的计算，既然是a[0...i]构造最大数字，那么 a[i]是一定要选用的（这儿需要一定的推理，a[i]构造数字时，相邻的j个是不能同时用的，就像上述的2、3不能构造出5一样，推理请自己完成），那么要选用的下一项只能递减寻找，直到找到 a[t] 满足 a[t] * K < a[i] ，而b[t]就是a[0...t]所能构造的最大数字，再加上a[i], 即为a[0...i]能构造的最大数字，于是b[i] = b[t] + a[i]。
求得数列后，之后的工作就简单了，跟Fibonacci博弈一样一样的，如果n=数列中的数，则必败，否则必胜；必胜时还要求输出第一步取法，按照上文的理解，将n分解之后，选择最小的一个a[i]即可（类似选择二进制的最小的1）。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int k;
int flag = 0;
LL a[N], b[N];
int main() {
int T;
scanf("%d", &T);
int cases = 0;
while (T--) {
cases++;
LL m, n;
cin >> n >> m;
a[0] = b[0] = 1;
int i = 0, j = 0;
while (n > a[i]) {
i++;
a[i] = b[i - 1] + 1; //首先求出当前的a数组
while (a[j + 1] * m < a[i]) j++;
if (a[j] * m < a[i])
b[i] = b[j] + a[i]; //然后根据a数组求b数组
else
b[i] = a[i];
}
if (n == a[i])
printf("Case %d: lose\n", cases);
else {
LL res = a[i];
while (n) {
if (n >= a[i]) n -= a[i];
res = a[i];
i--;
}
printf("Case %d: %lld\n", cases,res);
}
}
return 0;
}
HDU 4315 Climbing the Hill
大意：
有N个人爬山，山顶坐标为0，其他人的坐标按升序给出。不同的坐标只能容纳一个人（山顶不限），Alice和Bob轮流选择一个人让他移动任意步，但不能越过前面那个人。现在有一个人是king（给出id），谁能将king移动到山顶就算赢。
思路：
和poj1704很类似，从下往上把每两个点分成一组，组内两点的间隔可以看成奇数阶层的石子数，组间的间隔可以看成偶数阶层的石子数，因为如果移动组内前面的点，那么下一轮可以移动组内后面的点同样的距离保持平衡态，如果移动组内后面的点，那么下一轮可以移动其它组后面的点，这样就变成了阶梯博弈。
不同的是有几个特殊情况，当k为1的时候一定是先手必胜， 当n为奇数k为2的时候，第一个点没人愿意移动到终点，所以最终态提前了一格，即a[0]变成了1。
还需要注意的是，因为本题中移动到0号点是可行的，所以当0和a[1]配对时，不需要-1，所以可设a[0] == -1，这样就不需要写特判了
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n, k, a[N];
int main() {
while (scanf("%d%d", &n, &k) != EOF) {
a[0] = -1;
for (int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + n + 1);
if (k == 1)
cout << "Alice" << endl;
else {
int sg = 0;
if (k == 2 && (n % 2 == 1)) {
a[0]=0;
for (int i = n; i >= 1; i -= 2) {
sg ^= (a[i] - a[i - 1] - 1);
}
} else {
for (int i = n; i >= 1; i -= 2) {
sg ^= (a[i] - a[i - 1] - 1);
}
}
if (sg)
cout << "Alice" << endl;
else
cout << "Bob" << endl;
}
}
return 0;
}
HDU 1538 A Puzzle for Pirates
大意：
这是一个经典问题，有n个海盗，分m块金子，其中他们会按一定的顺序提出自己的分配方案，如果50%或以上的人赞成，则方案通过，开始分金子，如果不通过，则把提出方案的扔到海里，下一个人继续。现在给出n，问第k个海盗（第n个海盗先提方案，第1个最后提方案）可以分到多少金子，还是会被扔到海里去。
思路：
首先我们讲一下海盗分金决策的三个标准：保命，拿更多的金子，杀人，优先级是递减的。
同时分为两个状态稳定状态和不稳定状态:如果当n和m的组合使得最先决策的人(编号为n)不会被丢下海, 即游戏会立即结束, 就称这个状态时"稳定的". 反之, 问题会退化为n-1和m的组合, 直到达到一个稳定状态, 所以称这种状态为"不稳定的".
接下来我们从简单的开始分析：
如果只有两个人的话：那么2号开始提出方案，这时候知道不管提什么，他自己肯定赞成，大于等于半数，方案通过，那么2号肯定把所有的金子都给了自己。
如果只有三个人的话：那么3号知道，如果自己死了，那么2号肯定能把所有金子拿下，对于1号来说没有半点好处。那么他就拿出金子贿赂1号，1号拿到1个金子，总比没有好，肯定赞成3号，剩下的3号拿下。
如果只有四个人的话：那么4号知道，如果自己死了，那么1号拿到1个金子，2号什么都没有，3号拿下剩下的金子。那他就可以拿出部分金子贿赂2号，2号知道如果4号死了，自己将什么都没有，他肯定赞成4号。
如此类推下去，如果n<=2*m时候，前面与n相同奇偶性的得到1个金子，剩下的第n个人全部拿下。
但是会有一个问题便是，如果金子不够贿赂怎么办：
我们将问题具体化：如果有500个海盗，只有100个金子，那么前面200个已经分析过了。
对于201号来说，拿出100个金子贿赂前面的第200号分金子时拿不到金子的100个人。自己不拿金子，这样刚好有101票保证自己不死，如果分给之前能拿到金子的人，那么之前拿不到金子的人反正无论如何也拿不到金子，不如把你杀了。
对于202号来说，自己不能拿金币，而贿赂上一轮没有拿到金币的101人中的100人就够了，这样凑齐101票。
对于203号来说，需要102个人的支持，显然加上他自己，还需要101票，而金子不够贿赂，别人会反对，而达到杀人的目的。所以这时其他人会分到多少金子是未知的，只知道203号会被扔进海里，也就是说现在是“不稳定的”状态，会退化到202号来分100个金子的状态，那么其他人得到的金子就遵循202号的方案。
对于204号来说，他知道一旦自己死了，203号是必死，抓住这点，203必然支持他，因为203号宁可不要金币，也要保住性命，所以204号把100个金币分给之前的100个人，然后203和他自己的两票保证自己不死。
对于205号来说，203，和204是不会支持他的，因为一旦205死了，他们不仅可以保住性命，而且还可以看着205死掉。所以205是必死
那么206呢，虽然205必死，会支持他，但是还是缺一票，所以必死。
对于207呢，205和206之前是必死，会支持他，但是加上自己以及100个贿赂名额，还是必死
对于208号，205，206.，207因为后面是必死的，肯定会支持208成功，那么208刚好能凑齐104票，得以保命
所以可以得到结论：只有当n == 2 * m + 2^i的时候Pn能保命,否则在第一个2 * m + 2^i之前的海盗都会死亡
但是当n大于 2 * m + 1时，活下来的人分到的金子是不确定的，以202为例：到第202海盗的时候，除了自己刚好需要100个人支持，如果按照前面的当然给2 -- 200中偶数号海盗，但是假如他给201号海盗的话，他也会支持，因为假如202号丢进海里，自己分的话他是得不到的，所以他能拿到金子，当然也支持202号，所以这样就有101个人只要得到金子就一定会支持，所以虽然存活与否是能够确定的，但是分得金子是不确定的，要么是0要么是1，但是不过本题中要求输出海盗可以获得的最少金子数量，也就是说此时输出0即可。
所以归纳一下：
当n<=2 * m时：
与n奇偶性相同的获得1，不同的获得0，然后剩下的全部由n号海盗获得
当n==2 * m+1时
第n个人为0，奇数号的人为1，偶数号的人为0
当n>2 * m+1时
设位置满足2 * m + 2 ^ i的最大的位置为k，大于k的全部扔到海里，其他人获得金子是不确定的，输出0
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int t, a[30];
int main() {
cin >> t;
for (int i = 0; i <= 20; i++) a[i] = pow(2, i);
while (t--) {
int n, m, k;
cin >> n >> m >> k;
if (n <= 2 * m) {
if (k == n)
cout << m - (n - 1) / 2 << endl;
else {
if (k % 2 == n % 2)
cout << 1 << endl;
else
cout << 0 << endl;
}
}
else if(n==2*m+1){
if (k % 2 == 1&&k!=n) cout << 1 << endl;
else
cout << 0 << endl;
}
else {
int flag = 0, pos = 0;
for (int i = 0; i <= 20; i++) {
if (2 * m + a[i] <= n) {
pos = i;
}
}
if (k > 2 * m + a[pos]) {
cout << "Thrown" << endl;
}
else{
cout << 0 << endl;
}
}
}
return 0;
}
HDU 3404 Switch lights
大意：
在一个n+1行m+1列的表格里，坐标从(0,0)标记到(n,m)，每一个格子中有一枚硬币，或正面朝上，或反面朝上。两个玩家轮流操作，每次操作同时翻4枚在一个矩形（边长平行于行列的矩形）四顶点的硬币，而且要求，其中行列坐标都较大的一枚硬币必须是从正面翻到反面的。即，当(x,y)正面向上的时候，可以同时翻(x,y)(x,b)(a,y)(a,b)（其中a<x，b<y）。双方如此不断操作，直至有一方无法操作为止，不能操作的人负，即不能操作的状态（只有第0行和第0列有正面向上的硬币，或者整个表格的硬币都反面向上）是胜利终止状态。
思路：
nim积模板题，但是看不懂...丢个板子在这吧
#include <bits/stdc++.h>
#define N 2000000
using namespace std;
int m[2][2] = {0, 0, 0, 1};
int Nim_Mult_Power(int x, int y) {
if (x < 2) return m[x][y];
int a = 0;
for (;; a++)
if (x >= (1 << (1 << a)) && x < (1 << (1 << (a + 1)))) break;
int m = 1 << (1 << a);
int p = x / m, s = y / m, t = y % m;
int d1 = Nim_Mult_Power(p, s);
int d2 = Nim_Mult_Power(p, t);
return (m * (d1 ^ d2)) ^ Nim_Mult_Power(m / 2, d1);
}
int Nim_Mult(int x, int y) {
if (x < y) return Nim_Mult(y, x);
if (x < 2) return m[x][y];
int a = 0;
for (;; a++)
if (x >= (1 << (1 << a)) && x < (1 << (1 << (a + 1)))) break;
int m = 1 << (1 << a);
int p = x / m, q = x % m, s = y / m, t = y % m;
int c1 = Nim_Mult(p, s), c2 = Nim_Mult(p, t) ^ Nim_Mult(q, s),
c3 = Nim_Mult(q, t);
return (m * (c1 ^ c2)) ^ c3 ^ Nim_Mult_Power(m / 2, c1);
}
int main() {
int t, n, x, y;
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
int ret = 0;
while (n--) {
scanf("%d%d", &x, &y);
ret ^= Nim_Mult(x, y);
}
if (ret)
puts("Have a try, lxhgww.");
else
puts("Don't waste your time.");
}
return 0;
}
