ICPC 2018 Nanjing Regional
A. Adrien and Austin
大意:
一共n个数,每次可以取至少1个至多k个连续的数,先手胜输出Adrien,后手胜输出Austin
思路:
当k=1时,直接根据n的奇偶性判断即可
当k大于等于2时,先手总可以先取中间的1个或者2个,使得两边剩下的数量一样多,这样后手怎么选我就选和他对称的即可,这样先手必胜
注意当n=0时先手必败的特判即可
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n, k;
int main() {
cin >> n >> k;
if (n == 0) {
cout << "Austin" << endl;
return 0;
}
if (k == 1) {
if (n % 2 == 0)
cout << "Austin" << endl;
else
cout << "Adrien" << endl;
} else {
cout << "Adrien" << endl;
}
return 0;
}
D. Country Meow
大意:给出空间上的n个点,求出一个点的位置,使得到这个点距离最远的点的距离最小
思路:最小球覆盖问题, 和平面上的做法类似,直接套板子即可
#include <bits/stdc++.h>
using namespace std;
int const N = 100 + 5;
const double inf = 2e7;
double ans = inf;
int n;
struct node {
double x, y, z;
} a[N];
double getd(node a, node b) {
double dx = a.x - b.x;
double dy = a.y - b.y;
double dz = a.z - b.z;
return sqrt(dx * dx + dy * dy + dz * dz);
}
double getsum(node x) { // f函数
double re = 0;
for (int i = 0; i < n; i++) {
re = max(re, getd(x, a[i]));
}
ans = min(ans, re);
return re;
}
double rand(double l, double r) { //计算一个l到r的随机值
return (double)rand() / RAND_MAX * (r - l) + l;
}
void sa() {
node p{rand(-1e5, 1e5), rand(-1e5, 1e5), rand(-1e5, 1e5)};
for (double t = 2e5; t > 1e-4; t *= 0.99) {
node np{rand(p.x - t, p.x + t),
rand(p.y - t, p.y + t),rand(p.z - t, p.z + t)}; //随机一个新的点
double dt = getsum(np) - getsum(p); //计算能量差
if (exp(-dt / t) >
rand(0, 1)) { //如果是求最大值,则exp(dt / t) > rand(0, 1)
p = np;
}
}
}
int main() {
cin >> n;
srand((unsigned)time(NULL));
for (int i = 0; i < n; ++i) {
cin >> a[i].x >> a[i].y >> a[i].z;
}
//for (int i = 0; i < 100; ++i) sa();
while ((double)clock() / CLOCKS_PER_SEC < 0.8) sa();
printf("%.5lf\n", ans);
}
G. Pyramid
大意:
求出n层三角形中,三角形的数量:
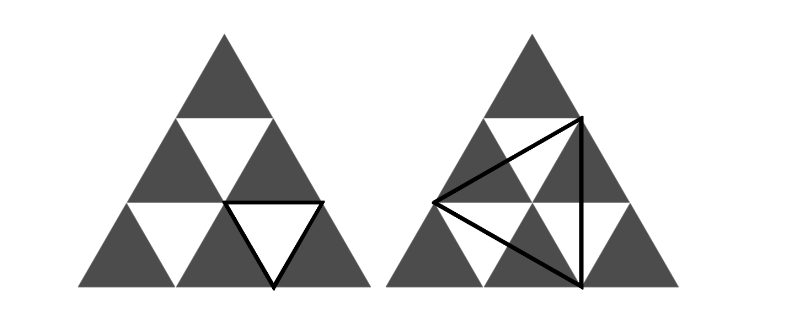
思路:
打表找规律,发现数量是\(\frac{n*(n+1)*(n+2)*(n+3)}{24}\)
直接求即可,注意需要求24的逆元
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL mod = 1e9 + 7;
LL powmod(LL a, LL b) {
LL res = 1;
while (b) {
if (b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
int main() {
LL T;
cin >> T;
LL inv24 = powmod(24, mod - 2);
while (T--) {
LL n;
scanf("%lld", &n);
LL Ans = n * (n + 1) % mod;
Ans = Ans * (n + 2) % mod;
Ans = Ans * (n + 3) % mod;
Ans = Ans * inv24 % mod;
printf("%lld\n", Ans);
}
}
I. Magic Potion
大意:
n个英雄,m个怪兽,k个技能
每个英雄有各自可以打败的怪兽,每个英雄只能打一个怪兽
每个英雄都可以用一次技能额外击败一个怪兽
问最多可以击败多少个怪兽
思路:
最大流,每个英雄入度为1,每个怪兽出度为1,然后英雄和怪兽连线,另外每个英雄有一个相应的“魔法英雄”,英雄的源点入度为n,魔法英雄的源点入度为k
#include <bits/stdc++.h>
using namespace std;
int const N = 1e5 + 20, M = 2e5 + 10, INF = 1e9 + 10;
int e[M * 2], ne[M * 2], h[N], f[M * 2], idx, k;
int d[N], cur[N], n, m, S, T;
void add(int a, int b, int c) {
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}
// bfs找是否存在增广路
int bfs() {
queue<int> q;
memset(d, -1, sizeof d);
q.push(S);
d[S] = 0;
cur[S] = h[S];
while(q.size()) {
int t = q.front();
q.pop();
for (int i = cur[t]; ~i; i = ne[i]) {
int j = e[i];
if (d[j] != -1 || !f[i]) continue;
d[j] = d[t] + 1; // 更新分层图
cur[j] = h[j]; // 当前弧优化,cur[j]记录j点第一条可以访问的边
if (j == T) return 1;
q.push(j);
}
}
return 0;
}
// dfs把增广路更新
int find(int u, int limit) {
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]) { // 当前弧优化+流量限制
cur[u] = i;
int j = e[i];
if (d[j] != d[u] + 1 || !f[i]) continue; // 必须在分层图上,防止出现环;必须有流量
int t = find(j, min(f[i], limit - flow)); // 找到从j出去的流量
if (!t) d[j] = -1; // 流量为0,说明这条路不行
f[i] -= t, f[i ^ 1] += t, flow += t; // 更新流量
}
return flow;
}
int dinic() {
int res = 0, flow = 0;
// 每次判断是否存在增广路(bfs),如果存在,那么把所有的增广路更新(find)
while (bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m >> k;
S = 0, T = 2 * n + m + 1;
for (int i = 1, t; i <= n; ++i) {
cin >> t;
for (int j = 1, mon; j <= t; ++j) {
cin >> mon;
add(i, 2 * n + mon, 1);
add(n + i, 2 * n + mon, 1);
}
}
for (int i = 1; i <= n; ++i) add(S, i, 1);
for (int i = 1; i <= m; ++i) add(2 * n + i, T, 1);
add(S, 2 * n + m + 2, k);
for (int i = 1; i <= n; ++i) add(2 * n + m + 2, n + i, 1);
printf("%d\n", dinic());
return 0;
}
J. Prime Game
大意:
给出n个数的数组,问这个数组的所有区间的 元素的积的素因子的个数和是多少
思路:
分别对每个素因子考虑贡献
对于一个素因子来说,记录其出现的位置,那么它全部的贡献可以由\(n*(n+1)/2\)减去每个没有出现的小区间的贡献组成

如图为例,贡献可表示为\(n*(n+1)/2-d_0*(d_0+1)/2-d_1*(d_1+1)/2-d_2*(d_2+1)/2-d_3*(d_3+1)/2\)
但是仅仅想出这个还不行,暴力会超时
一个优化的方法是先将1到1e6的数全部分解质因数,然后对于输入的数,直接看它的质因子有哪些, 并标记出现的位置,计算贡献
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> PII;
LL const N = 1e6 + 10;
unordered_map<LL, vector<LL>> mp;
unordered_map<LL, LL> sum;
vector<LL> num[N];
LL prime[N];
LL st[N];
LL cnt = 0;
void get_prime(LL n) {
for (LL i = 2; i <= n; ++i) {
if (!st[i]) {
prime[cnt++] =
i; // 如果这个数字没有被记录,那么这个数字必然为素数,记录一下
num[i].push_back(i);
}
for (LL j = 0; prime[j] <= n / i; ++j) {
st[prime[j] * i] = true; // 筛掉pj*i这个合数
if (i % prime[j] == 0)
break; // i%pj==0,说明pj是i的最小素因子,因此i*素数的最小素因子也是pj,在i递增的时候也会被筛掉,因此不需要在这里判断
}
}
for (LL i = 0; i < cnt; i++) {
for (LL j = 1; j <= n; j++) {
if (j * prime[i] > n) break;
num[j * prime[i]].push_back(prime[i]);
}
}
}
int main() {
get_prime(1e6);
LL n;
scanf("%lld", &n);
for (LL i = 1; i <= n; i++) {
LL x;
scanf("%lld", &x);
for (LL j = 0; j < num[x].size(); j++) {
LL p = num[x][j];
mp[p].push_back(i);
LL d;
if (mp[p].size() == 1)
d = i - 1;
else
d = i - mp[p][mp[p].size() - 2] - 1;
sum[p] += d * (d + 1) / 2;
}
}
LL ans = 0;
for (auto it = mp.begin(); it != mp.end(); it++) {
LL d = n - (it->second)[(it->second).size() - 1];
ans += n * (n + 1) / 2 - (sum[it->first] + d * (d + 1) / 2);
}
printf("%lld\n", ans);
return 0;
}
K. Kangaroo Puzzle
大意:
给出一个地图,每个1上面都有一个袋鼠,每个0都是墙,现在要求给出一个不长于5e4的字符串,全体袋鼠按照这个字符串的方向移动,不会穿过墙,问能否最后汇聚到一个点上
思路:
看题解才知道可以利用随机化莽过去....因为地图很小,而字符串很长,所以随机移动有很大的几率使得袋鼠汇聚到一点
不过也是要看运气的,a数组一开始写的LRUD就没过,改成ULRD就过了.....真的玄学
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
char a[4] = {'U', 'L', 'R', 'D'};
int main() {
srand(time(0));
int n, m;
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
char x;
cin >> x;
}
}
for (int i = 0; i < 50000; i++)
cout << a[int(double(rand()) / RAND_MAX * 3.0 + 0.5)];
cout << endl;
return 0;
}

