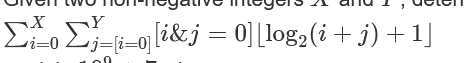2020 ICPC 上海(8/13)
A Wowoear
大意:
思路:
B Mine Sweeper II
大意:
输入两个扫雷的地图,要求只改变(m*n/2)个点,使得第二个图上面每一个点的数字和与第一个图相同
思路:
这个题太cf了....
想了很久最后发现直接将原图翻转,点变成叉 叉变成点,然后直接在原图和翻转的图上修改即可,这样总能保证有一个图的修改数量是小于(m*m/2)的
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
int const N = 2e3 + 10;
int n, m, T;
int a[N][N], b1[N][N], b2[N][N];
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
string s;
cin >> s;
for (int j = 0; j < s.size(); j++) {
if (s[j] == 'X')
a[i][j] = 1;
else
a[i][j] = 0;
}
}
for (int i = 0; i < n; i++) {
string s;
cin >> s;
for (int j = 0; j < s.size(); j++) {
if (s[j] == 'X')
b1[i][j] = 1, b2[i][j] = 0;
else
b1[i][j] = 0, b2[i][j] = 1;
}
}
int sum1 = 0, sum2 = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (a[i][j] != b1[i][j]) sum1++;
if (a[i][j] != b2[i][j]) sum2++;
}
}
int k = (n * m) / 2;
if (sum1 <= k) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if(a[i][j])cout<<'X';
else cout<<'.';
}
cout<<endl;
}
}
else if(sum2<=k){
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if(a[i][j])cout<<'.';
else cout<<'X';
}
cout<<endl;
}
}
else cout<<-1<<endl;
return 0;
}
C Sum of Log
大意:
给出两个数x和y,求出:
思路:
可以看出后面的式子就是\(x|y\)的最高位
数位DP,直接分别枚举x和y每一位作最高位的情况
\(dp[pos][limit1][limit2]\)代表pos做最高位,x和y是否达到上界
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int numx[32], numy[32], lx, ly;
LL dp[32][2][2];
const LL mod = 1e9 + 7;
LL dfs(int pos, int limit1, int limit2) {
if (pos == -1) return 1;
//这里直接将limit1和limit2记忆化了,否则会超时
if (dp[pos][limit1][limit2] != -1) return dp[pos][limit1][limit2];
int up1, up2;
if (limit1)
up1 = numx[pos];
else
up1 = 1;
if (limit2)
up2 = numy[pos];
else
up2 = 1;
LL res = 0;
for (int i = 0; i <= up1; i++) {
for (int j = 0; j <= up2; j++) {
if ((i & j) == 1) continue;
res += dfs(pos - 1, limit1 && (i == up1), limit2 && (j == up2));
res %= mod;
}
}
dp[pos][limit1][limit2] = res;
return res;
}
LL solve(int x, int y) {
lx = 0;
memset(numx, 0, sizeof numx); //这里必须清空!!
memset(numy, 0, sizeof numy);
memset(dp, -1, sizeof dp);
while (x) {
numx[lx++] = x % 2;
x /= 2;
}
ly = 0;
while (y) {
numy[ly++] = y % 2;
y /= 2;
}
LL res = 0;
for (int i = 0; i < lx; i++) {
res += dfs(i - 1, i == (lx - 1), i >= ly) * LL(i + 1);
res %= mod;
}
for (int i = 0; i < ly; i++) {
res += dfs(i - 1, i >= lx, i == (ly - 1)) * LL(i + 1);
res %= mod;
}
return res;
}
int main() {
int x, y, t;
memset(dp, -1, sizeof dp);
cin >> t;
while (t--) {
cin >> x >> y;
cout << solve(x, y) << endl;
}
return 0;
}
D Walker
大意:
一条长度为n的路,现在给出两个人所在的位置,再给出两个人步行的速度,问两个人将这条路全部走完最短需要多久
思路:
分类讨论:
第一个人直接走完全程
第二个人直接走完全程
第一个人向右走,第二个人向左走
二分分割点pos,第一个人走0到pos,第二个人走pos到n
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
double n, v1, v2, p1, p2, res;
int t;
bool check(double pos) {
res = min(res, max(min(p1 + pos, pos - p1 + pos) / v1,
min(n - p2 + n - pos, p2 - pos + n - pos) / v2));
return min(p1 + pos, pos - p1 + pos) / v1 >
min(n - p2 + n - pos, p2 - pos + n - pos) / v2;
}
int main() {
scanf("%d", &t);
while (t--) {
res = 0x3f3f3f3f;
cin >> n >> p1 >> v1 >> p2 >> v2;
if (p1 > p2) {
swap(p1, p2);
swap(v1, v2);
}
// p1走完全程
res = min((min(p1, n - p1) + n) / v1, res);
// p2走完全程
res = min((min(p2, n - p2) + n) / v2, res);
// p1向右走到底 p2向左走到底
res = min(res, max((n - p1) / v1, p2 / v2));
// p1走0到pos,p2走pos到n
double l = p1, r = p2;
while (r - l > 1e-8) {
double mid = (l + r) / 2;
if (check(mid)) { // p1走的慢,需要把分割点向左移
r = mid;
} else {
l = mid;
}
}
printf("%.7lf\n", res);
}
return 0;
}
E The Journey of Geor Autumn
大意:
思路:
F Fountains
大意:
思路:
G Fibonacci
大意:
给一个数n,要求输出\(\sum_{i=1}^{n}\sum_{j=i+1}^{n}g(f_i,f_j)\)
如果x乘y为偶数,则g为1,否则为0
思路:
在纸上找找规律就行了,统计奇偶数即可
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
int const MAXN = 2e5 + 10;
int n, m, T;
int main() {
cin >> n;
LL res = 0;
LL cnt = n / 3 ;
res = cnt * (cnt - 1);
if (n % 3 == 1) res += cnt;
else if (n % 3 == 2) res += cnt * 2;
res += (1 + cnt) * cnt / 2 * 3 - cnt;
cout << res;
return 0;
}
H Rice Arrangement
大意:
长度为n的环形桌子,k盘菜,k个人,问最少转动几次桌子可以让每个人都吃上菜
思路:
一个推论:第一个人选择菜之后,后面的人都是按顺序吃,否则答案不是最优(产生的交叉)
所以可以枚举第一个人选择哪盘菜,然后求答案即可
但是转桌子可以有三种选择:
顺时针转到底
逆时针转到底
选择一个点x作为分割点,先逆时针再顺时针,或者先顺时针后逆时针
所以再枚举这三种情况即可
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
typedef long long LL;
int t, n, k;
LL a[N], b[N], c[N];
LL res;
void solve(int x) {
for (int i = 0; i < k; i++) {
c[i] = (a[(i + x) % k] - b[i] + n) % n;
} //求出对应位置的距离
sort(c, c + k);
res = min(res, c[k - 1]); //顺时针
res = min(res, n - c[0]); //逆时针
for (int i = 0; i < k - 1; i++) { //先顺后逆或先逆后顺
res = min(res, 2LL * c[i] + n - c[i + 1]);
res = min(res, 2LL * (n - c[i + 1]) + c[i]);
}
}
int main() {
cin >> t;
while (t--) {
res = 0x3f3f3f3f3f3f3f;
cin >> n >> k;
for (int i = 0; i < k; i++) {
cin >> a[i];
}
for (int i = 0; i < k; i++) {
cin >> b[i];
}
sort(a, a + k);
sort(b, b + k);
for (int i = 0; i < k; i++) {
solve(i);
}
cout << res << endl;
}
return 0;
}
I Sky Garden
大意:
给出两个数n和m,分别代表同心圆的数量,和直线的数量,同心圆的间隔都是1,直线平均分每个圆,问这些图形的交点之间的距离之和
思路:
因为是对称的,所以先想一条线与圆的交点,到其他所有的点的距离,对于一个圆上的直接算即可,因为只有两条路,要么是经过圆心到达目的地,要么是沿着小弧到达。而不是同一个圆上的点,我们可以先将外面的圆上的点移动到内圆上,然后再直接求距离(因为相比于将内圆上的点移动到外圆上,这样的移动更优)
最后要考虑只有一条线的情况
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const double PI = acos(-1);
int const MAXN = 5e5 + 10;
double num[MAXN];
double sum[MAXN];
int n, m, T;
int main() {
cin >> n >> m;
double O = m * n * (n + 1);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (j == m)
num[i] += 2 * i;
else
num[i] += 2 * min(2.0 * i, j * PI * i / m);
}
}
double ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
sum[i] += num[i] + 2 * (j - i) * m;
}
sum[i] *= 2 * m;
ans += sum[i];
ans += num[i] * m;
}
if (m == 1)
printf("%.10lf\n", ans);
else
printf("%.10lf\n", ans + O);
return 0;
}
J Octasection
大意:
思路:
K Traveling Merchant
大意:
思路:
L Traveling in the Grid World
大意:
给出\(n*m\)的网格,从(0,0)点开始,每次可以走到一个点(x,y),但是两点之间的连线不能有其他格点,走任意次,问走到(n,m)的最少距离是多少
思路:
一个结论是如果\(gcd(n,m)==1\)那么可以从\((0,0)\)直接走到\((n,m)\)而不经过其他格点,所以如果\(gcd(n,m)==1\),那么可以直接求答案,而如果不等于1,可以找到一个点\(gcd(x,y)==1\)且\(gcd(n-x,m-y)==1\),然后转移过来,但是不能枚举每个点,这样会超时,贪心的想,最佳的路线是对角线,而对角线上下左右一个点的位置必然有可以转移的点,那么枚举这些点即可,复杂度为O(n)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int t,n, m;
const int inf = 0x3f3f3f3f;
double cal(int x, int y) {
if (!(x >= 0 && x <= n && y >= 0 && y <= m)) return inf;
if (!(__gcd(x, y) == 1 && __gcd(n - x, m - y) == 1)) {
return inf;
}
if (n * y == m * x) return inf;
return sqrt(1.0 * x * x + 1.0 * y * y) + sqrt(1.0 * (n-x) * (n-x) + 1.0 * (m-y) * (m-y));
}
int main() {
cin >> t;
while (t--) {
double res = inf;
cin >> n >> m;
if (__gcd(n, m) == 1)
res = sqrt(1.0 * n * n + 1.0 * m * m);
else
for (int i = 0; i <= n; i++) {
int j = i * m / n;
res = min(res, cal(i, j));
res = min(res, cal(i, j - 1));
res = min(res, cal(i, j + 1));
}
printf("%.10lf\n", res);
}
return 0;
}
M Gitignore
大意:
给出两个数n和m,先给出n个需要被ignore的文件的路径,然后再给出m个不应该被ignore的文件的路径,要求输出ignorelist最少可以是多少项(也就是问ignore的文件可以被合并成最少几个路径)
思路:
根据输入的路径进行建树,然后根据输入的m个文件对路径进行标记,这个文件所处的路径一路都打上标记,最后暴力dfs即可,遇到没有被标记的文件夹就返回,代表可以被合并成一个文件夹,否则就继续向下搜
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
int const MAXN = 2e5 + 10;
int n, m, T;
unordered_map<string, int> mp;
string s[MAXN];
int tag[MAXN];
int e[MAXN], ne[MAXN], idx, h[MAXN];
int cnt = 0;
int mapping(string s) {
if (!mp.count(s)) mp[s] = ++cnt;
return mp[s];
}
map<PII,int>exist;
void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++; }
LL res = 0;
void dfs(int u, int fa) {
if (!tag[u]) {
res++;
//cout<<mp2[u]<<endl;
return;
}
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
dfs(j, u);
}
return;
}
void build() {
for (int i = 1; i <= n; ++i) {
int last = 0;
string tmp = "";
for (int j = 0; j < s[i].size(); ++j) {
tmp += s[i][j];
if (s[i][j] == '/'){
if(!exist.count({last,mapping(tmp)}))
add(last, mapping(tmp)),exist[{last,mapping(tmp)}]=1;
last = mapping(tmp);
}
}
add(last, mapping(tmp));
//tag[mapping(tmp)]=1;
}
}
int main() {
cin >> T;
while (T--) {
res = 0;
mp.clear();
exist.clear();
memset(tag, 0, sizeof tag);
idx = 0;
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; ++i) cin >> s[i];
for (int i = 1; i <= m; ++i) {
string ss;
cin >> ss;
string tmp = "";
for (int j = 0; j < ss.size(); ++j) {
tmp += ss[j];
//cout<<tmp<<endl;
if (ss[j] == '/') tag[mapping(tmp)] = 1;//cout<<tmp<<endl;
}
}
build();
tag[0]=1;
dfs(0, -1);
cout << res << endl;
}
return 0;
}