An interpretation of depth value
An Interpretation of Depth Value
Recently when I am working on Screen Space Reflection, I noticed there are some subtleties in the computation of depth value.
In this article I will explain the deeper meaning in the computation of depth value.
Perspective Projection Matrix
First, it is well known that the DirectX perspective projection matrix is:
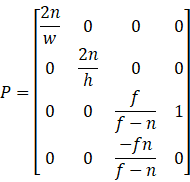
In this matrix:
is width of
the screen
is height of
the screen
is near
clipping plane
is far
clipping plane
All these values are measured in view space.
Since DirectX uses row vector, the z and w component are:
After perspective division, the actual depth value is:
But what does it mean? Is there any deeper meaning in it? Why not use a simpler one, like linear interpolation?
The answer to the second question is yes.
To dive into the deeper meaning, first we
express 
as an expression
of 
,
we get:
Something interesting happens! The depth value is linear interpolation weight for the reciprocals of near and far value!
Sounds great, but who cares? Yes, in most cases, you don’t need to care about that. However, in some specific case, it will bring you a lot of convenience. Screen space reflection is an example.
Ray Marching in Screen Space
In screen space reflection, one need to perform ray marching and find the intersection of a ray and depth buffer. Of course, ray marching can be performed in view space, but it’s difficult to choose a proper step size because the same step size in view space appear smaller and smaller when the ray is moving away from the camera. Alternatively, performing ray marching in screen space can avoid this problem because you can choose the step size based on the pixel size. However, as the depth value is a non-linear function of z value in view space, the step size for depth value is not constant. If you use the projection matrix to calculate the depth value based on the x and y values in every step, that will cause a lot of computation. Is there a fast way to calculate the depth value? Yes! And the linear interpolation nature of the reciprocal of depth value is the heart of this method.
To explain this, I would like to formulate
the problem first. Suppose you know the view space coordinates of the both ends
of a line segment AB, denoted as 
and
.
The projection matrix is also known, so you can calculate their screen space
coordinates 
and
.
You want to perform linear interpolation on image plane with 
the
interpolation weight. The xy coordinate of point C is easy:
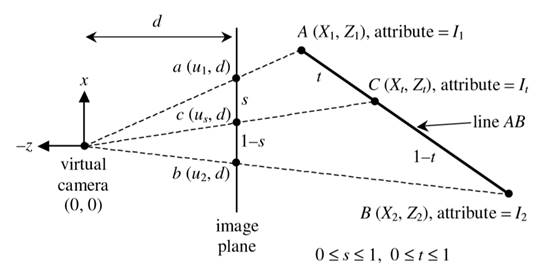
But how
can I get 
conveniently,
given ? I can
calculate given
, it’s
So, the next step is to know the relationship between s and t.
Now let’s look at the picture below, it’s the equivalent version of the last picture.
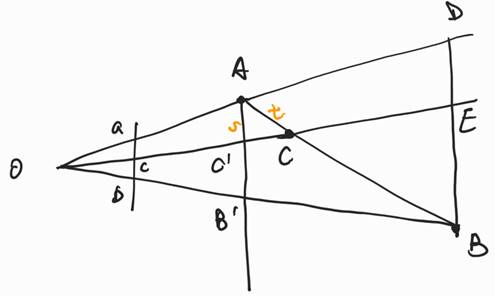
Let
,
.
Then we have:
Also, we know
and
Put them together, we have
Put it
into ,
we have:
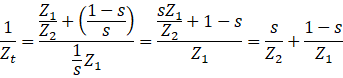
Finally, we get
That is
to say, instead of using to
linear interpolate ,we can use to
linear interpolate 
!
We’ve already use to linear
interpolate xy coordinate. If we consider as
a special coordinate axis. So, in the (x’, y’, 1/z) coordinate space, every
axis can be linear interpolated!
Why is the depth value like that?
From the first section, we know the depth value is the linear interpolation weight for the reciprocal of near and far value.
From the second section, we know (x’, y’, 1/z) can be linear interpolated.
Then we have
That
means linearly
interpolates depth value, and in the (x’, y’, depth) coordinate space
(screen space), every axis can be linear interpolated.
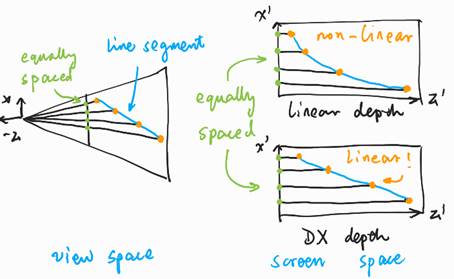
To show the benefit of this, let’s see the picture above, suppose there is a line segment in view space, if we choose a naïve depth (for example, using the z component in view space directly), the line segment will become a curve in (x’, y’, depth) space. However, by using DirectX depth (OpenGL depth is similar), the line segment will be still a line segment!
Things that appear straight/planar in view space, will also appear straight/planar in screen space. That is the idea behind the depth computation formula.
附件列表
