一、scipy库的LP
scipy库官方文档:Linear Programming
官方文档例子
利用官方的lingprog:API介绍
1.1 线性规划
利用官方的API的标准形式如下:
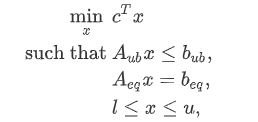
- 最小化目标函数
- 约束条件是小于等于 或者 等于
- 转化为矩阵的形式
1.2 linprog
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='interior-point', callback=None, options=None, x0=None)[source]
例子
官方文档例子:
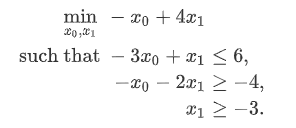
在这个例子中,需要转化为小于等于的形式,那么第2个约束条件转化为:\(x_0+2x_1 \leq 4\),第3个约束条件转化为 \(-x_1 \leq 3\)。
由于 目标是\(cx\),条件是\(A_{ub}x \leq b_{ub}\), bound是每个变量的范围,则x1的bound为\((-3,\text{None})\), 那么:
\(A_{ub} = [[-3,1][1,2]]\)
\(c=[-1,4]\)
\(b=[6,4]\)
c = [-1, 4]
A = [[-3, 1], [1, 2]]
b = [6, 4]
x0_bounds = (None, None)
x1_bounds = (-3, None)
from scipy.optimize import linprog
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds])
output:
print(res)
con: array([], dtype=float64)
fun: -21.99999984082494 # may vary
message: 'Optimization terminated successfully.'
nit: 6 # may vary
slack: array([3.89999997e+01, 8.46872439e-08] # may vary
status: 0
success: True
x: array([ 9.99999989, -2.99999999]) # may vary
1.3 API使用的算法
线性规划的解决算法一般有两种:
(1) revised simplex (2) interior-point
两种算法的思想有所差别。如果在使用过程中需要修改,想获得更高的accuracy,那么可以使用revise simplex,调用方法:
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='revised simplex')
simplex核心思想是:首先找到约束条件范围一个顶点,然后求解当前顶点目标函数值;然后按照目标函数值增长最快的方式路径来选择附近的其他顶点;一直找邻近的其他顶点直到目标函数值不再增长。
interior point算法:不同的地方在于不局限于找顶点,而是在整个范围内都可以找,就像梯度下降一样,可以在范围内部找目标函数值最大的点,直到目标函数值不值增长。
留下的问题:
LP两种算法的核心思想了解了,若想知道具体细节,可以去youtube看看具体步骤和实现。
二、Pulp
源码:github
官方文档:doc
环境要求:Python 2.7 or Python >= 3.4.
pulp定义了这么多class:
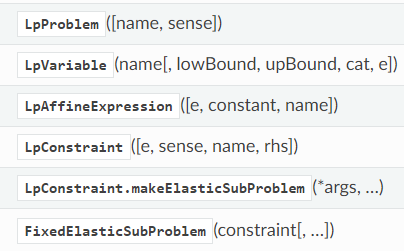
2.1 安装:
可以使用pip安装 或者pypi来安装。pip安装命令如下:
python -m pip install pulp
如果想安装最新版本则:
python -m pip install -U git+https://github.com/coin-or/pulp
测试安装(Linux \ OSX):
sudo pulptest
2.2 plup解决LP的步骤
(1)首先创建所有变量的范围,如:
\(x\),这个变量的约束条件是 \(0 \leq x \leq 3\)
\(y\),这个变量的约束条件是 \(0 \leq y \leq 1\)
x = LpVariable("x", 0, 3)
y = LpVariable("y", 0, 1)
(2)然后创建线性规划对象: 这个对象是最小化问题,最后对象为prob
prob = LpProblem("myProblem", LpMinimize)
(3)约束条件和目标函数都可以用\(+=\) 加在prob里面:
prob += x + y <= 2 #约束条件
prob += -4*x + y #目标函数
(4)slove这个问题
status = prob.solve()
(5)可以查看solve后的状态 以及查看每个变量的值
LpStatus[status] #'Optimal'
value(x) #2.0
2.3 slover 算法
用其他的slover来解决上述LP优化问题,只需要将prob.slove()添加参数即可,例如
status = prob.solve(GLPK(msg = 0))
PuLP can generate MPS or LP files and call GLPK, COIN-OR CLP/CBC, CPLEX, GUROBI, MOSEK, XPRESS, CHOCO, MIPCL, SCIP to solve linear problems.
例子
from pulp import *
problem = LpProblem("basicP",LPMaximize) #最大化目标函数
#变量比较多,不一一定义,可以用LpVariable.dicts
c = [20,12,40,25]
x_cnt = len(c)
x = pulp.LpVariable.dicts('x',range(x_xnt),lowBound=0) #返回{0:x_1, 1:x_2, 2:x_3, 3:x_4}
#目标函数 sum([c[i]*x[i])
problem += lpSum([c[i]*x[i] for i in range(x_cnt)])
A = [[1,1,1,1],[3,2,1,0],[0,1,2,3]]
b = [50,100,90]
#用lpSum把约束条件一起加进去。 lpSum相当于处理矩阵的方式,拆开来看就是+=操作
for i in range(len(b)):
problem += lpSum([x[j]*A[i][j] for j in range(x_cnt)] <= b[i], f"Constraint:{i}"
#可以打印看看constraints:
#problem.constraints
#problem
#解决上述定义好的问题
problem.solve()
problem.status
for v in problem.variables():
print(v.name,"=",v.varValue)
print(problem.objective)
export function
- value() -- Finds the value of a variable or expression
- lpSum() -- given a list of the form [a1*x1, a2x2, ..., anxn] will construct a linear expression to be used as a constraint or variable
- lpDot() --given two lists of the form [a1, a2, ..., an] and [ x1, x2, ..., xn] will construct a linear epression to be used as a constraint or variable



