说明：主要参考资料来源于cs860

在本节中，我们介绍差分隐私，首先我们会介绍Warner提出的第一个差分隐私算法[1]。

一、Randomized Response

问题描述

问题： 假设自己是一个班级的老师，这个班级有一场考试，但是这场考试有很多人作弊，但是自己不确定多少人作弊。那怎么你怎么能计算出有多少学生作弊呢？（当然学生肯定不会老实承认自己作弊了）

将问题抽象出来：有\(n\)个人，每个人\(i\)有个私密的数据\(X_i \in \{ 0,1 \}\)，他们确保其他人不知道自己的这个私密数据\(X_i\)到底是0还是1。但是为了配合分析师分析所有人的数据，每个人\(i\)根据自己的私密数据\(X_i\)和一些自己产生的随机数来产生一个\(Y_i \in \{ 0,1 \}\) ，然后向分析师发送一个消息\(Y_i\)。最后分析师根据收到的所有的\(Y_i\)来得到一个概率估计:

\[p=\frac{1}{n}\sum_{i=1}^nX_i \]

这样分析师就大概知道这里面大概有多少人的\(X_i\)是0，多少人的\(X_i\)是1了。

在上述问题中，可以抽象为：\(X = \sum_{X_i}^n\),其中\(X_1,X_2...X_n\)是相互独立的，且\(Pr(X_i = 1)=p_i\),\(Pr(X_i=0)=1-p_i\)。(即有\(n\)种期望分别为\(p_i\)的伯努利分布)
令\(p = \mu = \mathbb{E}(X) = \frac{1}{n}\sum_{i=1}^nX_i\)

如何生成随机数

（1）我们先假设所有人都说的是真话，每个人只可能说真话。意思是个体\(i\)的隐私数据\(X_i\)是多少，那就向分析师发送的数据是多少。那么分析师收到的\(Y\)值就等于\(X\):

\[Y_{i}=\left\{\begin{array}{ll}X_{i} & \text { with probability } 1 \\ 1-X_{i} & \text { with probability } 0\end{array}\right. \]

那么可以得到：\(\tilde{p}=\frac{1}{n} \sum_{i=1}^{n} Y_{i}\)，实际上：\(p = \tilde{p}\)。但是虽数值准确，但是分析师可以确切知道大家都说的真话，因此明确地知道了每个人的\(X_i\)值。那么应该如何既保证个体的隐私，又让分析师能计算出真实的\(p\)值呢？
（2）如果每个人都有一半可能说真话，一半可能说假话，\(Y_i\)的均值是1/2，意思是，每个人如果多次发送的话，期望都是1/2，那么分析师分析的数据\(Y\)完全独立于\(X\)，两个变量之间没有相关性，那么其实收集到的数据就是个二项分布：

\[Y_{i}=\left\{\begin{array}{ll}X_{i} & \text { with probability } \frac{1}{2} \\ 1-X_{i} & \text { with probability } \frac{1}{2}\end{array}\right. \]

，即每人说自己是0还是1的概率与其本身不符合。这样虽然确保证了每个人的隐私，但是数据完全不真实，没有可用性。
（3）Randomized Response策略：如果让每个人有一半以上的概率说真话，一半以下的概率说假话，那么分析师不知道具体到个人具体到底说的话到底是真话还是假话（一半以下的概率虽然小一些但是也有可能发生），则保证了个体数据的隐私性。即：基于一个参数\(\gamma \in [0,1/2]\)

\[Y_{i}=\left\{\begin{array}{ll}X_{i} & \text { with probability } \frac{1}{2}+\gamma \\ 1-X_{i} & \text { with probability } \frac{1}{2}-\gamma \end{array}\right. \]

注意到： \(\gamma = 0\)的时候就和第二种情形一样，\(\gamma = \frac{1}{2}\)的时候和第一种一样。
因此，不能从个体的\(Y_i\)推断出真实的\(X_i\)是什么值，因此个体隐私得到了保护。
此时，我们可以计算出分析师收到的\(Y_i\)的期望是：

\[\mathbb{E}[Y_i] = [\frac{1}{2}+\gamma]X_i + [\frac{1}{2}-\gamma][1-X_i] = 2\gamma X_i +\frac{1}{2} -\gamma \]

然后通过上式转换，计算\(X_i\)的期望：$$\frac{\mathbb{E}[Y_i] - \frac{1}{2} + \gamma}{2 \gamma} = \mathbb{E}[X_i]$$
可以理解为\(x_i\)的估计值与收到的\(Y_i\)的关系如上式所示。然后将所有的人（一共n个）累加起来可以得到：

\[\mathbb{E}[\tilde{p} ]= \frac{1}{n} \sum_{i = 1}^n [\frac{1}{2 \gamma} (Y_i-1/2+ \gamma)] \]

然后计算\(\mathbb{E}[\tilde{p}]\):

\[\operatorname{Var}[\tilde{p}]=\operatorname{Var}\left[\frac{1}{n} \sum_{i=1}^{n}\left[\frac{1}{2 \gamma}\left(Y_{i}-1 / 2+\gamma\right)\right]\right]=\frac{1}{4 \gamma^{2} n^{2}} \sum_{i=1}^{n} \operatorname{Var}\left[Y_{i}\right] \leq \frac{1}{16 \gamma^{2} n} \]

最后一步的不等式是由切比雪夫不等式推导得出的。(也可以用切诺夫界得到更精确的Bound）。当\(n\)趋于无穷大时，这个误差偏差趋近于0。

二、差分隐私的介绍

  • 现在我们介绍差分隐私，有时候也被称为\(\text{central differential privacy}\)或者\(\text{trusted curator }\)模型。

假设有n个个体，其数据点分别服从n种独立随机变量\(X_1,X_2...X_i\)，他们都有自己的数据点，然后他们都信任curator不信任其他人。、
这个curator运行一个算法\(M\)，对于给定的输入数据，会公开输出计算结果。

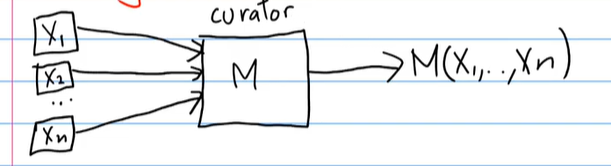
差分隐私就是一种算法，这种算法可使得：任何一个个体的数据对整体输出结果来说，没有大的影响和改变。就是说\(X_i\)改变了，但是输出不会很大的改变。下面给出差分隐私的正式的定义：

算法\(M:\mathcal{X}^{n} \rightarrow \mathcal{Y}\),其中任意两个数据集\(X,X^{\prime} \in \mathcal{X}^n\),这两个数据集只有一个（行）数据不一样，我们将这两个数据集称为 neighbouring datasets（相邻数据集），可以记为\(X \sim X^{\prime}\)。
对于所有的相邻数据集\(X,X^{/prime}\) 和所有的\(T \subseteq \mathcal{Y}\) ，我们称算法\(M\)是 \(\varepsilon\) -(pure) differentially private ( \(\varepsilon\) -(pure) DP):

\[Pr[M(X) \in T] \leq e^{\varepsilon} Pr[M(X^{\prime}) \in T] \]

其中M的选择是随机性的。

上述的定义是2006年的Dwork, McSherry, Nissim, and Smith的论文中给定的定义，现在被广泛接受和用于数据的隐私保护....

对于差分隐私：

-Dierential privacy是定量的。\(\varepsilon\)越小则隐私性越强，反之隐私性越弱。

  • \(\varepsilon\)应该被认为是一个小的常数。在0.1和5之间的任何东西都可能是一个合理的隐私保障水平（更小的对应着更强的隐私），明显超出这一范围的值就需要考虑和怀疑一下下这个值的合理性了。

  • \(\varepsilon\) 是对所有相邻数据集\(X \sim X^{\prime}\)的最大偏差的一个Bound,保证其最坏的情况也在\(\varepsilon\)之内。

差分隐私分为两种:
(1) bound differential privacy, 是交换、改变数据集里面的一条数据
（2）unbound differential privacy, 是add/remove数据集里面的一条数据
交换，改变数据集里面的一条数据相当于做了两次改变，因此是和增加、删除是不一样的，在数学层面上他们的Number不一样的，对于Bound dp也是复杂一些。我们再对比时候需要比较到底是unbound dp还是bound dp。

下面接着会有一系列差分隐私的笔记，希望自己能学好，记录好~

引用文献

[1]Stanley L. Warner. Randomized response: A survey technique for eliminating evasive
answer bias. Journal of the American Statistical Association, 60(309):63{69, 1965.