绝大部分内容都来自:浅谈「正定矩阵」和「半正定矩阵」
若侵权则删除
浅谈「正定矩阵」和「半正定矩阵」
在众多的机器学习模型中,线性代数的身影无处不在,当然,我们也会时常碰到线性代数中的正定矩阵和半正定矩阵。例如,多元正态分布的协方差矩阵要求是半正定的。
--------------×--------------×--------------
1. 基本的定义
正定和半正定这两个词的英文分别是positive definite和positive semi-definite,其中,definite是一个形容词,表示“明确的、确定的”等意思。
初学线性代数的读者可能会被这两个词“唬住”,但正定矩阵和半正定矩阵的定义实际上是很简单的 (不考虑复数构成的矩阵):
【定义1】给定一个大小为 \(n \times n\) 的实对称矩阵 \(A\) ,若对于任意长度为\(n\) 的非零向量\(x\) ,有\(\boldsymbol{x}^{T} A \boldsymbol{x}>0\)恒成立,则矩阵\(A\)是一个正定矩阵。
【例1】单位矩阵\(I \in \mathbb{R}^{2 \times 2}\)是否是正定矩阵?
解:设向量\(\boldsymbol{x}=\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right] \in \mathbb{R}^{2}\) 为非零向量,则
\(\boldsymbol{x}^{T} \boldsymbol{I} \boldsymbol{x}=\boldsymbol{x}^{T} \boldsymbol{x}=x_{1}^{2}+x_{2}^{2}\)
由于 \(\boldsymbol{x} \neq \mathbf{0}\) ,故 \(\boldsymbol{x}^{T} I \boldsymbol{x}>0\) 恒成立,即单位矩阵\(I \in \mathbb{R}^{2 \times 2}\)是正定矩阵。
单位矩阵是正定矩阵 (positive definite)。
对于任意单位矩阵\(I \in \mathbb{R}^{2 \times 2}\)而言,给定任意非零向量 \(\boldsymbol{x} \in \mathbb{R}^{n}\) ,恒有
\(\boldsymbol{x}^{T}Ix =\boldsymbol{x}^{T} \boldsymbol{x} = =x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}>0\)
【例2】 实对称矩阵 \(A=\left[\begin{array}{ccc}2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2\end{array}\right] \in \mathbb{R}^{3 \times 3}\)是否是正定矩阵?
解:设向量\(\boldsymbol{x}=\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right] \in \mathbb{R}^{3}\)为非零向量,则
\(\boldsymbol{x}^{T} A \boldsymbol{x}=\left[\left(2 x_{1}-x_{2}\right) \quad\left(-x_{1}+2 x_{2}-x_{3}\right) \quad-x_{2}+2 x_{3}\right]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right]\)
\(=x_{1}^{2}+\left(x_{1}-x_{2}\right)^{2}+\left(x_{2}-x_{3}\right)^{2}+x_{3}^{2}>0\)
理解:\(X\)是一个\(n\)维向量,那么\(\boldsymbol{x}^{T} A \boldsymbol{x}\)相乘的结果其实就是二次型,那么\(f(X) = \boldsymbol{x}^{T} A \boldsymbol{x}>=0\)则是一个二次齐次函数,如果\(X\)为2维,则是二元二次函数。那么这个对称矩阵就是这个二元二次函数的参数。则,使得二元二次函数取值恒大于0的参数矩阵,就是正定的(大于等于0,则是半正定)。
每个二次型都唯一对应一个对称矩阵。
【定义2】给定一个大小为 \(n \times n\) 的实对称矩阵 \(A\) ,若对于任意长度为 \(n\) 的向量 \(x\) ,有 \(\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0\) 恒成立,则矩阵\(A\) 是一个半正定矩阵。
根据正定矩阵和半正定矩阵的定义,我们也会发现:半正定矩阵包括了正定矩阵,与非负实数 (non-negative real number)和正实数 (positive real number)之间的关系很像。
正实数与负实数,图片来源于https://en.wikipedia.org/wiki/Real_number
2.从二次函数到正定/半正定矩阵
在初中数学中,我们学习了二次函数 \(y=a x^{2}\) ,该函数的曲线会经过坐标原点,当参数 \(a>0\)时,曲线的“开口”向上,参数 \(a<0\) 时,曲线的“开口”向下。
以 \(y=2 x^{2}\) 为例,曲线如下:
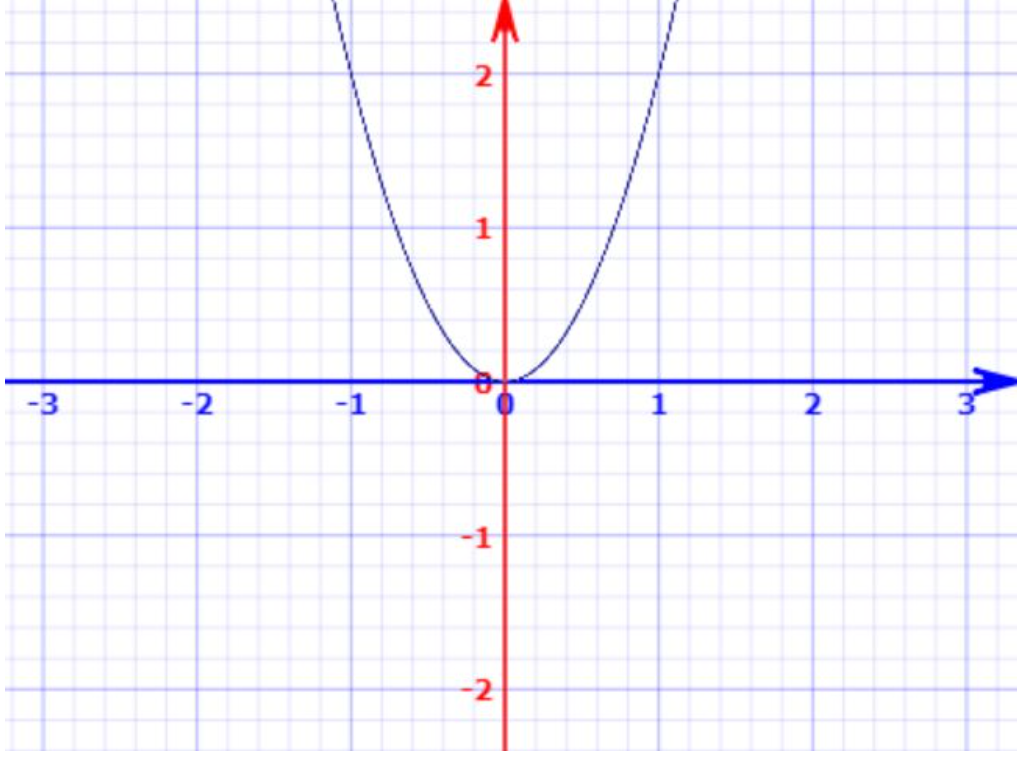
实际上,我们可以将 \(y=\boldsymbol{x}^{T} A \boldsymbol{x}\) 视作 \(y=a x^{2}\) 的多维表达式。
当我们希望 \(y=\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0\) 对于任意向量 \(x\) 都恒成立,就要求矩阵 \(A\) 是一个半正定矩阵,对应于二次函数, \(y=a x^{2}>0 ,\forall x\)需要使得 \(a \geq 0\) .
另外,在 \(y=a x^{2}\)中,我们还知道:若 \(a>0\) ,则对于任意 \(x \neq 0\),有 \(y>0\) 恒成立。
这在 \(y=\boldsymbol{x}^{T} A \boldsymbol{x}\)也有契合之处,当矩阵 \(A\) 是正定矩阵时,对于任意 \(\boldsymbol{x} \neq \mathbf{0}, \quad y>0\)恒成立。
3.正定矩阵和半正定矩阵的直观解释
若给定任意一个正定矩阵 \(A \in \mathbb{R}^{n \times n}\)和一个非零向量 \(\boldsymbol{x} \in \mathbb{R}^{n}\) ,则两者相乘得到的向量 \(\boldsymbol{y}=A \boldsymbol{x} \in \mathbb{R}^{n}\)与向量\(\boldsymbol{x}\)的夹角恒小于 \(\frac{\pi}{2}\) . (等价于:\(\boldsymbol{x}^{T} A \boldsymbol{x}>0\).)
【例3】给定向量 \(\boldsymbol{x}=\left[\begin{array}{l}2 \\ 1\end{array}\right] \in \mathbb{R}^{2}\) ,对于单位矩阵 \(I=\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right] \in \mathbb{R}^{2 \times 2}\) ,则
\(\boldsymbol{y}=I \boldsymbol{x}=\boldsymbol{x}=\left[\begin{array}{l}2 \\ 1\end{array}\right]\)
向量 \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^{2}\)之间的夹角为
\(\cos \langle\boldsymbol{x}, \boldsymbol{y}\rangle=\frac{\boldsymbol{x}^{T} \boldsymbol{y}}{\|\boldsymbol{x}\| \cdot\|\boldsymbol{y}\|}\)
\(=\frac{2 \times 2+1 \times 1}{\sqrt{2^{2}+1^{2}} \cdot \sqrt{2^{2}+1^{2}}}\)
\(=1\)
即两个向量之间的夹角为0°.
【例4】给定向量\(\boldsymbol{x}=\left[\begin{array}{l}1 \\ 2 \\ 1\end{array}\right] \in \mathbb{R}^{3}\) ,对于实对称矩阵 \(A=\left[\begin{array}{ccc}2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2\end{array}\right] \in \mathbb{R}^{3 \times 3}\) ,则
\(\boldsymbol{y}=A \boldsymbol{x}=\left[\begin{array}{l}0 \\ 2 \\ 0\end{array}\right]\)
向量\(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^{2}\)之间的夹角为
\(\cos \langle\boldsymbol{x}, \boldsymbol{y}\rangle=\frac{\boldsymbol{x}^{T} \boldsymbol{y}}{\|\boldsymbol{x}\| \cdot\|\boldsymbol{y}\|}=\frac{\sqrt{6}}{3}\)
即两个向量之间的夹角小于 \(\frac{\pi}{2}\) .
若给定任意一个半正定矩阵\(A \in \mathbb{R}^{n \times n}\) 和一个向量 \(x \in \mathbb{R}^{n}\) ,则两者相乘得到的向量\(y = Ax \in \mathbb{R}^n\) 与向量 \(x\) 的夹角恒小于或等于 \(\frac{\pi}{2}\) . (等价于: \(\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0\).) (上面是小于,这里是小于等于)
4.为什么协方差矩阵要是半正定的?
在概率论与数理统计中,我们都学习的协方差矩阵的定义:
对于任意多元随机变量 \(t\) ,协方差矩阵为
\(C = \mathbb{E}[(t - \bar{t})(t-\bar{t})^T]\)
现给定任意一个向量\(x\),则:
\(x^TCx = x^T \mathbb{E}[(t - \bar{t})(t-\bar{t})^T]x\)
\(=\mathbb{E}[x^T(t - \bar{t})(t-\bar{t})^Tx]\)
\(=\mathbb{E}(s^2) = \delta^2_s\)
其中,
\(\sigma_{s}=\boldsymbol{x}^{T}(\boldsymbol{t}-\overline{\boldsymbol{t}})=(\boldsymbol{t}-\overline{\boldsymbol{t}})^{T} \boldsymbol{x}\)
由于 \(\delta^2_s>0\) ,因此, \(\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0\) ,协方差矩阵\(C\) 是半正定的。