交点——软工第一次个人项目作业

1.在文章开头给出教学班级和可克隆的 Github 项目地址

项目	内容
这个作业属于哪个课程	2020春季计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里	个人项目作业
教学班级	005
github项目地址	https://github.com/trrrrht/IntersectProject.git

2.在开始实现程序之前，在下述 PSP 表格记录下你估计将在程序的各个模块的开发上耗费的时间。在你实现完程序之后，在下述 PSP 表格记录下你在程序的各个模块上实际花费的时间

PSP	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	5
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	120	200
· Design Spec	· 生成设计文档	30	50
· Design Review	· 设计复审 (和同事审核设计文档)	30	60
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	20
· Design	· 具体设计	30	40
· Coding	· 具体编码	60	90
· Code Review	· 代码复审	60	90
· Test	· 测试（自我测试，修改代码，提交修改）	30	50
Reporting	报告	20	30
· Test Report	· 测试报告	20	30
· Size Measurement	· 计算工作量	20	30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	20	30
	合计	470	725

3.解题思路描述。即刚开始拿到题目后，如何思考，如何找资料的过程

对于本题目，可以得知，最简单有效的想法就是将所读入几何图形记录，之后将其两两计算，得到交点坐标。之后将所有坐标两两比较，把重合的坐标去除，即可得到所要求的交点数目。

这样的思路对于基础部分，即\(1 \leq n \leq 1000\)来说，很轻松就可以在要求的时间范围内得到结果。但当数据量达到一定规模之后（经实验，取大致量级为\(10^5\)），已经无法达到要求的时间。

所以如果想在性能上面有一些起色，是需要进行大量的优化的。

对于优化，我找到了一个计算几何学中的算法，Bentley-Ottmann扫描线算法。

这个算法大致的思路是：

如果一个线段和另外一个线段有交点，那么用一条直线从上向下扫，可知有交点的线段一定是相邻的，如图所示：

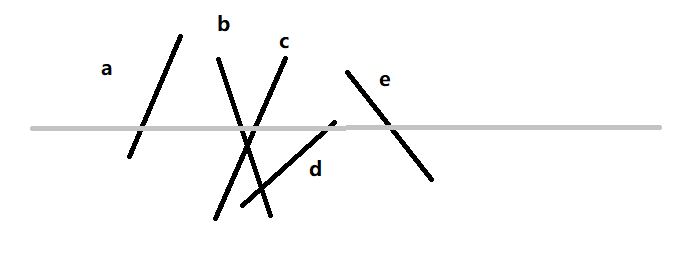
可以看出，bc交点之上，bc线段相邻。而有bd线段相交但不相邻的情况，这种情况下，当直线扫过bc交点，达到bd交点上时，可以知道bd是相邻的，所以通过这样的算法，就可以维护两个数据结构，得到交点个数：一条链表，用来记录所有线段的端点和已经找到的交点，每个点按y的递减顺序存储，若y相同，则按x递增顺序存储；一棵二叉树，负责记录与扫描线相交的线段，每条线段按照上端点的x坐标递增顺序存储。

如此，可以通过扫描线得到交点个数，算法时间复杂度为\(O((n+k)logn)\)，n为线段数量，k为焦点数量。

但这里有一个问题是，如果通过这种算法去算，是只能计算线段的交点个数的，而题目中要求是直线，所以我们无法找到直线的“上界”和“下界”，同时，对于附加题中的圆也是没有这种性质的。

这里仅提供一种思路，但是笔者暂时舍弃了这种做法。

所以最后采用的基础做法，还是直接暴力\(O(n^2)\)，但是由于太慢，所以研究了一些优化相关的问题。

同理，对于附加题部分的几何图形也是暴力\(O(n^2)\)。

4.设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？单元测试是怎么设计的？

显然，由于题目中要求支持直线和圆两种几何图形，那么需要的数据结构可以是结构体或者类。这两者的区别在与，类的实体可以自带函数，但是事实上，本次作业计算的应当是两两实体之间的性质，所以我仅仅使用了结构体来表示几何图形的基本属性。

之后通过计算的函数，将几何图形的实体作为参数传入，这样即可将交点计算出来。

对于交点的存储，我采取的方式是将交点的坐标封装为一个结构体，之后通过自己写键值和匹配方法来实现hash容器，以达到去重的目的。（最后更改为直接存入vector然后去重了）

各个函数的关系如下图所示：

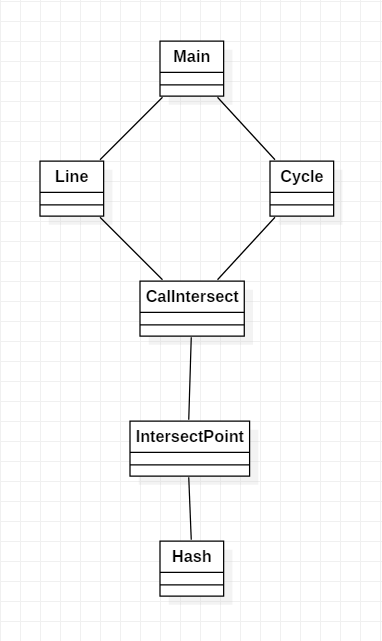
对于单元测试来说，考虑到几何图形中只包含直线和圆，那么需要考虑线与线的关系，线与圆的关系，圆与圆的关系三种不同的组合。

• 线与线关系
  • 相交
  • 垂直
  • 平行
• 线与圆关系
  • 相切
  • 相交
  • 相离
• 圆与圆关系
  • 相切
  • 相交
  • 相离
  • 内含

共十种不同的情况，在单元测试中需要全部覆盖。

覆盖率如图所示

5.记录在改进程序性能上所花费的时间，描述你改进的思路，并展示一张性能分析图（由 VS 2019 的性能分析工具自动生成），并展示你程序中消耗最大的函数。

由于附加题中圆的性质较难得出，所以下列优化的讨论仅限于直线部分。

公式计算

在一个平面内，对于仅包含两两相交的n条直线来说，其交点总个数计算公式为\(\frac{n*(n-1)}{2}\)。

但是对于本题目来说，其实是包含多个直线交于一点的情况的，所以就导致了总个数的计算公式中应该减去的情况包括：

• 平行的直线
• 交于一点的直线

而这两种情况中，对于平行直线的计算十分简单，只需要在读入数据的时候，将每一条数据的斜率计算出来，即可得到平行直线的数量。

所以现在主要的问题是如何得到多条直线交于一点的情况。

但是经过多次查阅资料，均无法较好的快速得出多条直线交于一点时，点的数量，所以这种做法实际上不可行。

分组

根据题目所给出的数据，最大数据输入量为500000，而交点个数最大为5000000，根据上述公式可以得知，题目所给数据中必定包含多个重合交点或者平行直线，大大减少了其交点个数。那么这样算来，可以通过两个方面来减少计算量。

• 平行分组
  • 这种做法的原理是通过将平行线不重复计算来减少计算量的。如果直接将所有直线两两计算交点，那么势必会有大量平行直线被遍历计算，所以，如果在读入数据的时候，根据直线的斜率将其分类成多个直线簇，可以减少直线簇内部的遍历，只需要计算直线簇之间的交点即可。
• 交点分组
  • 这种组佛啊的原理是通过将交于一点的直线不重复计算来减少计算量的。计算方式为，读入一条直线，计算其上是否存在已有交点，如果存在，此交点所代表的直线簇中的所有直线均不需要与该直线继续计算。基于此，可以减少对于同样交点直线的计算。

但是如上两种优化方式，经过实践可知，若想将直线分组，那么势必需要hash对交点或者斜率的映射，这样的话，占主要矛盾的部分反而不是对直线的遍历，而在于插入hash表时的计算，所以实际上看似会对性能有优化，其实是负优化。

多线程

对于多线程的考虑，最初来自于认为代码运行速度慢的主要矛盾在对于计算的遍历性，所以如果将线与线的相交，线与圆相交，圆与圆相交考虑的话，可以同时进行计算。但是这样其实只对附加题进行了优化，而如果将基础题的直线分组计算，很容易导致难以查出的bug，所以暂且没有进行尝试，仅仅提出一个可能可行的思路。

hash映射

对于hash映射部分，其实之前所讨论的优化已经用到了，但是效果均不太好，比如分组，比如交点，其原因在于，键值冲突时，c++的库函数所带hash容器计算量大增。但是，在最后计算交点重复的时候，需要两两对比交点，来刨去重合的交点。那么这就导致了主要矛盾在于交点之间比较的计算（交点最大个数为几何图形个数的十倍）。所以很自然的想到，如果将交点进行映射，查找复杂度为常数级，那么可以将其计算量大大节省。

所以我使用了c++库函数中支持hash的容器，在经过对比试验之后，发现速度与两两比较去重想比，大大加快。但是这样做，在大数据暴力测试的时候，又引发了新的问题。这个问题就是，插入hash容器的时候，由于键值增多，冲突便会不断增多，所以其复杂度从常数级，退化为log级乃至线性级。（后来发现其实用sort函数+unique去重的时间和用set的时间差异不大）

结构体和类

最初的时候，我设计的数据结构是通过结构体封装成Line和Cycle，将相关的信息存到里面去，同样的，类也可以做这样的操作。

但是在后来的实践中我发现，假如将参数直接放入数组索引，速度会相对较快一些，所以我仅保留了交点的结构体形式，将圆和直线全部拆为数组存储。

性能分析

如图所示，我随机生成了3000个数据点，交点个数为460W+，所用时为1.893s，其中消耗最大的函数为：

可以得知，我将set转换为vector之后再进行去重，成为制约程序性能的主要问题。

经过试验，如果数据量变大，那么制约其性能的主要问题则会变为对交点的计算，所以这样的性能制约其实是无法避免的。

6.代码说明。展示出项目关键代码，并解释思路与注释说明。

由于题目中实际上包含三种不同的计算，直线与直线，直线与圆，圆与圆

其中的直线与直线求交点的实现，采用的是一种较为简便的计算方法，即直线的一般式求交点法，如图所示：

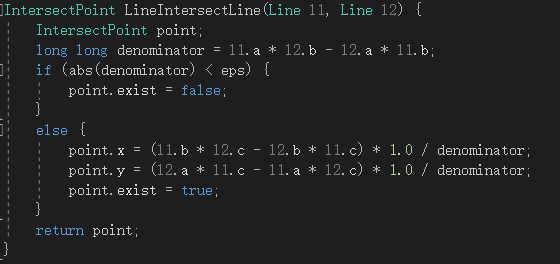
但直线与圆，圆与圆的交点计算并不十分容易。

所以对于直线与圆，我采取了一种向量法，这样可以较为简洁的计算出直线与圆的交点。

而圆与圆的计算公式即使使用了向量法，需要判断的条件也很多，所以，为了避免复杂计算的出错，我采取了一种较为取巧的方法，即将圆的一般公式输入到matlab，之后使用solve函数即可计算出其交点的坐标公式，这时，只需要判断根号下的数值是否存在，并且判断计算出的两点坐标是否相等，即可得到相应的坐标。唯一的问题是，虽然不需要判断很多条件，但是在输入计算公式的时候，一定要十分仔细，因为公式十分的长。

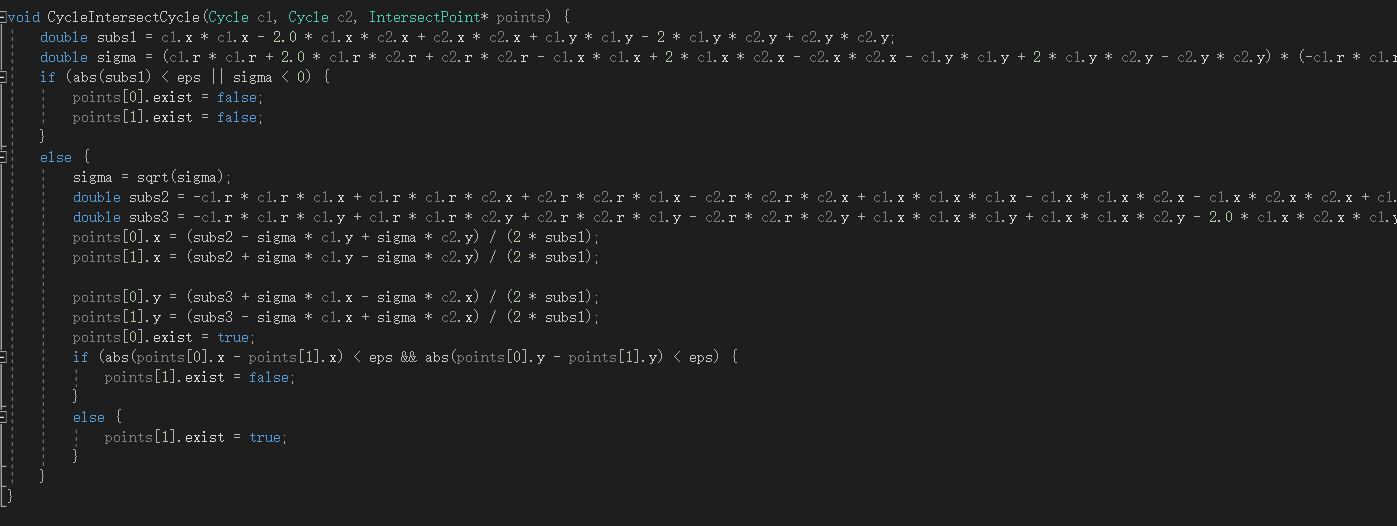
warning消除情况