buaaoo_third_assignment

你看这个代码它又长又宽

一、JML

　　（1）理论基础

　　　　JML(Java Modeling Language)是用于对Java程序进行规格化设计的一种表示语言。JML是一种行为接口规格语言（Behavior Interface Speciﬁcation Language，BISL），基于Larch方法构建。BISL提供了对方法和类型的规格定义手段。所谓接口即一个方法或类型外部可见的内容。JML主要由Leavens教授在Larch上的工作，并融入了Betrand Meyer，John Guttag等人关于Design by Contract的研究成果。近年来，JML持续受到关注，为严格的程序设计提供了一套行之有效的方法。通过JML及其支持工具，不仅可以基于规格自动构造测试用例，并整合了SMT Solver等工具以静态方式来检查代码实现对规格的满足情况。

　　　　一般而言，JML有两种主要的用法：
　　　　　　（1）开展规格化设计。这样交给代码实现人员的将不是可能带有内在模糊性的自然语言描述，而是逻辑严格的规格。
　　　　　　（2）针对已有的代码实现，书写其对应的规格，从而提高代码的可维护性。这在遗留代码的维护方面具有特别重要的意义。

　　（2）工具链

　　　　openjml使用SMT Solver来对检查程序实现是否满足所设计的规格(specification)。目前openjml封装了四个主流的solver，如图所示，可以进行配置。需要说明的是，我是在eclipse环境中安装的JML插件，IDEA中理应相同。

首先，JML工具没有自动下载和安装相应的solver，需要手动下载。我目前尝鲜了z3和cvc4。

　　　　z3由Microsoft开发的，并已在github上开源：https://github.com/Z3Prover/z3 其正式发布版可通过https://www.microsoft.com/en-us/download/details.aspx?id=52270获得。

　　　　cvc4由Standford开发，可以通过http://cvc4.cs.stanford.edu/downloads/下载。

二、SMT Solver

　　可以看出对于我部属的SMT来说，简单的方法它还是可以去识别并告知可能存在的错误的，但是对于比较复杂的方法，它可能与我们所学的规格有些不一样，所以无法正确识别。而老师也取消了第二个要求，所以姑且研究到这里。

三、JMLUnit

package demo;

public class Demo {
    /*@ public normal_behaviour
      @ ensures \result >= num1;
      @ ensures \result >= num2;
      @ ensures \result >= num3;
    */
    public static int compare(int num1, int num2, int num3) {
        int max;
        if (num1 > num2) {
            max = num1;
        }
        else {
            max = num2;
        }
        if (max < num3) {
            max = num3;
        }
        return max;
    }
    
    public static void main(String[] args) {
        compare(114,1919, 1111);
    }
}

　　采用test一个比较简单的方法来验证jmlunitng的实用性，通过伦佬的方法，运行了测试文件之后的结果是：

[TestNG] Running:
  Command line suite

Failed: racEnabled()
Passed: constructor Demo()
Passed: static compare(-2147483648, -2147483648, -2147483648)
Passed: static compare(0, -2147483648, -2147483648)
Passed: static compare(2147483647, -2147483648, -2147483648)
Passed: static compare(-2147483648, 0, -2147483648)
Passed: static compare(0, 0, -2147483648)
Passed: static compare(2147483647, 0, -2147483648)
Passed: static compare(-2147483648, 2147483647, -2147483648)
Passed: static compare(0, 2147483647, -2147483648)
Passed: static compare(2147483647, 2147483647, -2147483648)
Passed: static compare(-2147483648, -2147483648, 0)
Passed: static compare(0, -2147483648, 0)
Passed: static compare(2147483647, -2147483648, 0)
Passed: static compare(-2147483648, 0, 0)
Passed: static compare(0, 0, 0)
Passed: static compare(2147483647, 0, 0)
Passed: static compare(-2147483648, 2147483647, 0)
Passed: static compare(0, 2147483647, 0)
Passed: static compare(2147483647, 2147483647, 0)
Passed: static compare(-2147483648, -2147483648, 2147483647)
Passed: static compare(0, -2147483648, 2147483647)
Passed: static compare(2147483647, -2147483648, 2147483647)
Passed: static compare(-2147483648, 0, 2147483647)
Passed: static compare(0, 0, 2147483647)
Passed: static compare(2147483647, 0, 2147483647)
Passed: static compare(-2147483648, 2147483647, 2147483647)
Passed: static compare(0, 2147483647, 2147483647)
Passed: static compare(2147483647, 2147483647, 2147483647)
Passed: static main(null)
Passed: static main({})

===============================================
Command line suite
Total tests run: 31, Failures: 1, Skips: 0
===============================================

　　可以看出自动生成的数据包含了许多边界情况，这样可以对被测试的文件进行边界测试，至于常规数据测试，可以通过自己编写相关数据来运行，总的来说，jmlunitng还是比较方便的自动化测试工具，应该善加利用。

四、作业设计分析

　　（1）第一次作业

　　　　类图：

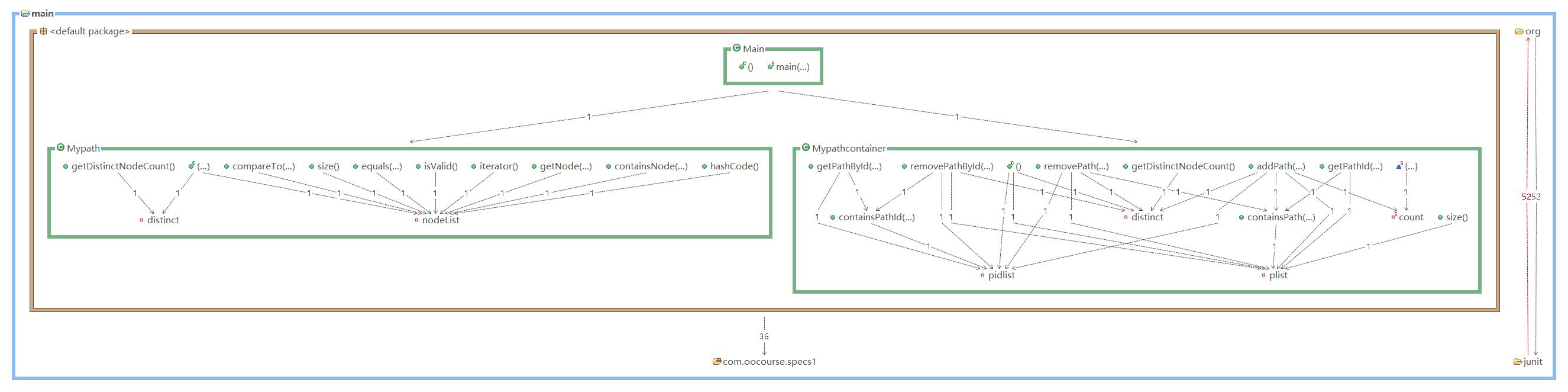
　　　　复杂度分析：

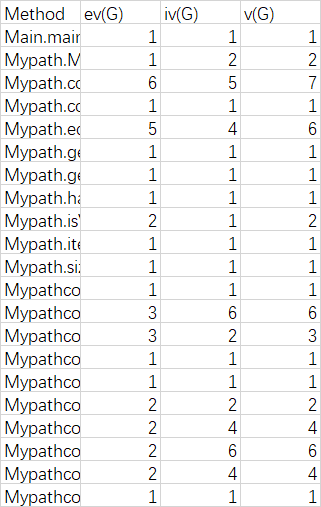
　　　　第一次作业可以说是没有难度，甚至根本不需要绞尽脑汁去优化，用最常规的写法就可以AC，而且写出的代码通常情况下都是十分简洁的，所以这里不做分析。

　　（2）第二次作业

　　　　类图：

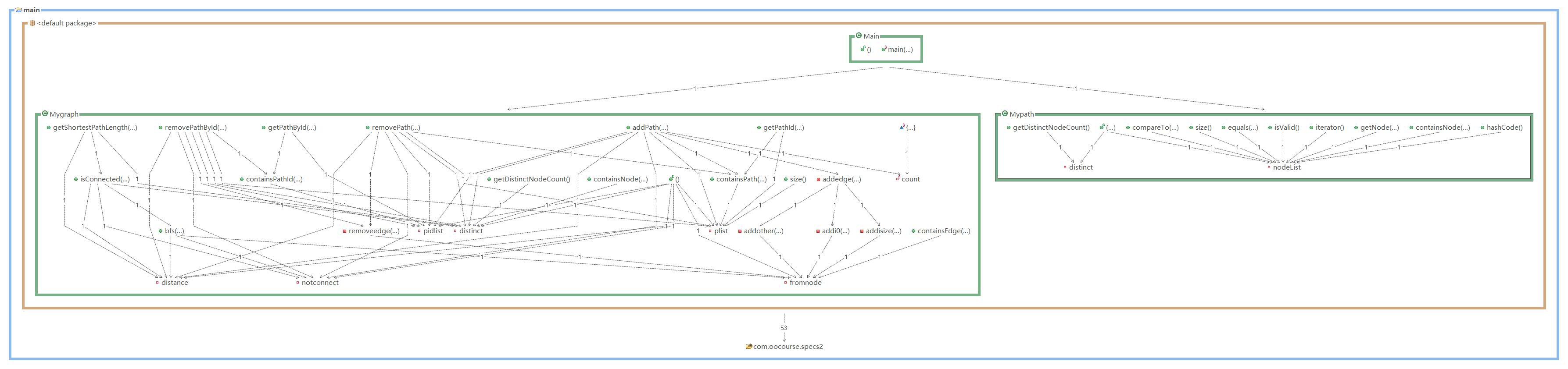
　　　　复杂度分析：

　　　　第二次作业比第一次作业稍微增加了一点思考，显然此次作业的难点就在于对最短路径求解的处理，我本人是通过BFS对fromid和toid进行求解，并且将沿路经过节点同时记录，这样会导致存储的最短路径越来越多，也就是说通过这样一个“cache”，可以大大提高求解的速度。（这里听说有同学用了floyd超时了，不太懂，估计是写丑了）其余部分中规中矩，按JML写就不会出错。

　　（3）第三次作业

　　　　类图：

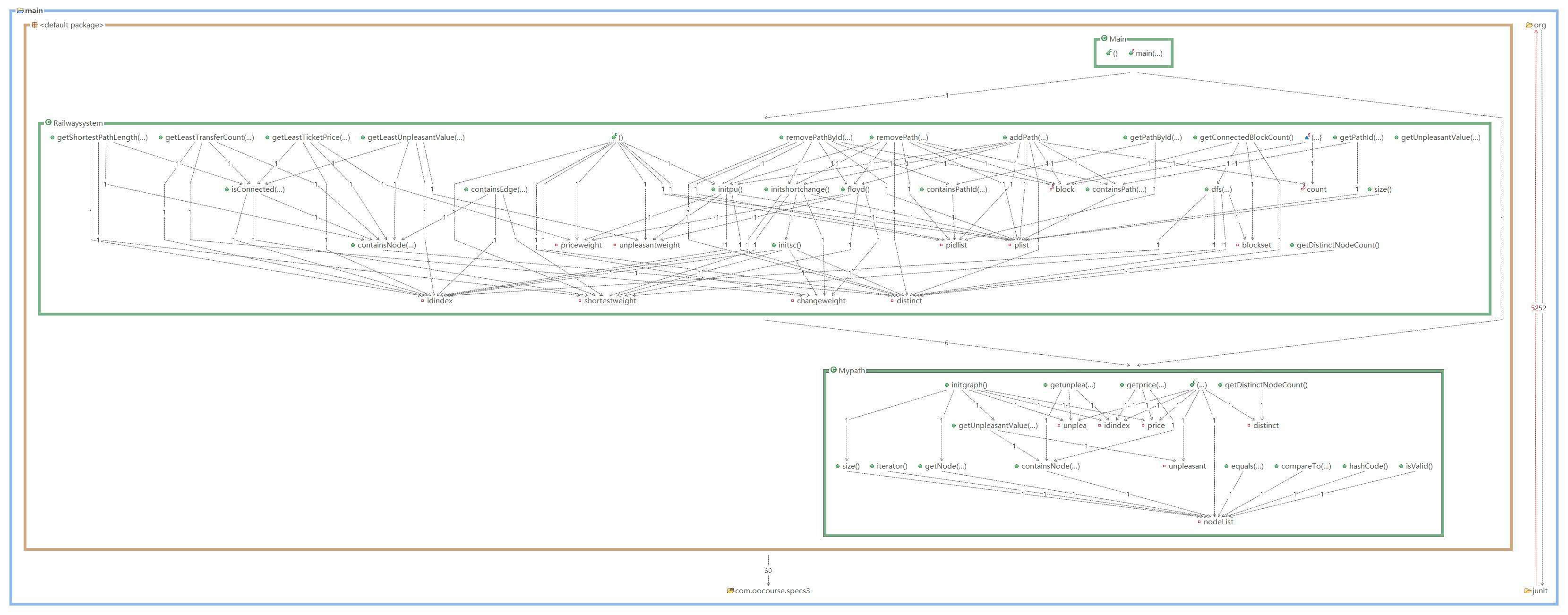
　　　　复杂度分析：

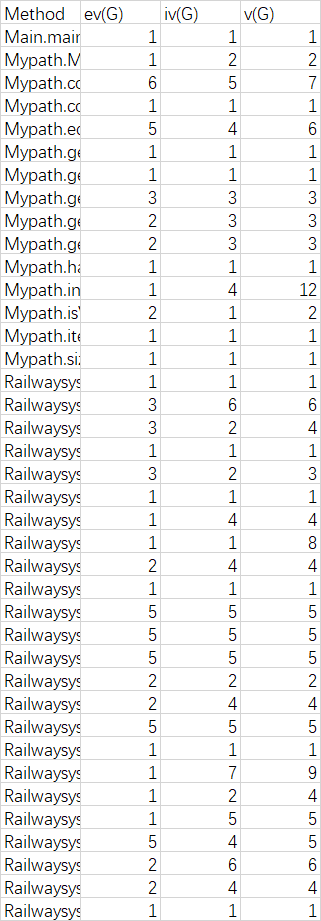
　　　　第三次作业着实坑了我一把，之前那么多次作业都没有写完了再重写的，这次作业我重写了三次才满意，具体经过如下，不带cache的不拆点法->未优化的拆点法->带cache的不拆点法，复杂度逐次降低到了我认为还可以的程度。这里面最令人费解的两个方法分别是求不满意度和求票价，其实这两个可以和求最少换乘算作一类题目，写出一个，另外两个就会写了，具体求解方法就是对每个路径内部求出两两点之间的最短路径，之后需要求解时，将其放入到总图中，利用floyd求解，则可以根据不同的权重得出各个方法的解。

　　　　最开始我没有想到将每个路径中添加它本身的最短路的图，所以就导致了我求解算法的时候需要对所有图重新遍历，复杂度大概是O（1250 * 120^3），这样一定会爆炸，所以我打算换成拆点法。拆点法的复杂度如果采用dijkstra的堆优化可以满足题目要求，但是我采用了数组存储的方式（因为直观好写），所以导致了复杂度是O（50 * 6000 * 6000），写完了之后才发现，然后还得重新写。听朋友讲了他的不拆点法有cache，我才知道将mypath中加入一个新的图，这样每次都可以存储，则复杂度只有O（100 * 120^3）可以说是大大降低了时间，我看了下，这种方法CPU time最多只有9s，可以说是十分不错的算法了（当然应该还可以继续优化）。

五、BUG相关

　　本单元三次作业都没有发现bug，不过每次作业我都写了评测机，在第二三次作业都找到了别人的bug，里面比较显著的bug就是在应用数组求解的时候，如果不注意映射关系的下标，可能会导致下标溢出报异常（第二次作业有两个老哥求最短路自己到自己都会错，差点以为自己凉了，结果发现他们是经验宝宝）。至于其它的错误，可能是算法错了，复杂度太高等，并没有深究。

六、感想与体会

　　通过对于JML的学习，我感觉到想对一个工程化的代码进行规约是一件很不容易的事情，而规约之后，如果方法特别复杂，也很难让人读懂。还有一个问题就是，如果想要清晰明白的表达方法所做的事情，就需要对于所写程序进行优化，但是这样就不免引入一个问题---JML的规范和优化冲突，我们知道，优化常常会让一些方法做本来不应该属于它们的事情，如果进行了大量优化，那么JML写起来就会更加晦涩难懂，而偏偏软件要保证性能，所以我姑且认为JML是对于框架的设计，实现一个裸代码，让人读懂需求之后再去进行优化。这单元三次作业都得了满分，这与大佬的帮助是分不开的，尤其是第三次作业，从最开始的根本不知道如何下手到方法太多，想重构无限次。总之，这次的JML之旅落下了帷幕，据说下一单元是UML，希望不会被坑掉。

就好像这个OO它又大又圆

posted @ 2019-05-21 23:32 有鹿阅读(180) 评论(0) 编辑收藏举报

刷新页面返回顶部

有鹿

🦌

buaaoo_third_assignment

公告