buaaoo_first_assignment
四周之前,我不懂面向对象是什么;四周之后,我依然不懂面向对象是什么。
一、第一次作业
(1)实现
说起来,本次作业是最惨烈的一次。
虽然它很简单,但由于未熟悉正则表达式的应用,导致判断wrong format使用了枚举法(即将表达式看成以合法字符组成的字符串,类似于自动机的手动判断某个字符接上某个字符是不合法的),着实耗费时间太久,而且在随后的互测中,因为未注意到指数部分的带符号整数的符号与数字间不能有空格,被狼人疯狂刀了十几下(讲真一个bug盯着咬也是醉了)。
而其实通过一个简易的正则表达式,可以大致将去除空白符后的项写为如下形式:
[+-]{0,2}(\\d+\\*x)?(x)?(\\d+)?(\\^[+-]?\\d+)?
之后便可以通过Matcher类中的find方法将每一个项提取出来之后,通过split,以x为分割点,就可以很容易的将每一项的系数与指数提取出来。最后以指数为key,系数为value装入Hashmap中,即可很容易的实现化简操作。
(2)经验
此次作业虽然简单,但是在强测中还是被hack了一个点,而在随后的互测中居然被hack了整整十九次,这是十分不应该的。
首先是强测中的bug,这个bug的起因是,Hashmap中,我的key与value的类型均是String,但输入的字符串包含了+-number,这样的带符号数字,甚至还有前导零,所以我在加入到Hashmap中时,无法判断+9与9是同样的指数,故而导致失分。此处仅将字符串数字通过Biginteger转化,即可实现错误的改正。
其次是互测中被hack的点,这在(1)中提到过,仅需要加入对于此Wrong Format的判断即可。
还有一个问题也比较严重,就是trim的应用,我直接在输入的表达式后用了这个方法,未能考虑到输入表达式首尾空白符不合法情况,导致失分。
二、第二次作业
(1)实现
这次作业我才开始尝试去熟悉OO所需要的实现方式,也就是面向对象,而非一个Main到底。(不过最后还是面向过程,真香)
我觉得此次作业一个比较大的进步是,尝试将一个Main函数分成几个类来进行不同的分工。这次分成了四个:输入,表达式处理,求导,输出,但事实上在表达式处理部分还是未能清晰的将层次结构梳理出来,也是一个比较遗憾的部分。
同样的,这次作业由于学会了错误的“大正则”方式,我将表达式化为了如下的正则(若无一行80字符限制我想很多人的正则表达式会比这个还恐怖,不要问我为什么知道):
(([+-]{0,3}\\d+)|([+-]{0,2}x(\\^[+-]?\\d+)?)|([+-]{0,2}sin\\(x\\)(\\^[+-]?\\d+)?)|([+-]{0,2}cos\\(x\\)(\\^[+-]?\\d+)?))(\\*(([+-]?\\d+)|(x(\\^[+-]?\\d+)?)|(sin\\(x\\)(\\^[+-]?\\d+)?)|(cos\\(x\\)(\\^[+-]?\\d+)?)))*
可以说如此冗(e)长(xin)的代码,不光成功的防止了互测阶段同学们读我的bug,也成功的让我自己恶心了一阵。虽然知道课程本以并不是让我们如此使用正则表达式,但在时间如此紧迫的情况下,写完就行。
由于加入了两个三角函数与项之间的乘积,所以在分项的方式上有了变化,最常用的有如下两种做法:
1、通过如上长正则,用group来直接提取出每一个小项
2、通过加减号分隔,也可以得到用group所提取出来的效果
笔者采用了第二种方式,而这也正是因为读了别人的第一次作业的代码,在此鸣谢某位不知名的大佬。通过split,将表达式以:
(?<![+\\-^*])[+\\-]
分隔,那么可以有效的避免指数中出现符号阻止项的正常分隔,不过这里值得注意的点是,由于通过加减号分隔,所以对于减号,需要查找到它被分隔的地方,手动添加回去。
之后就可以快乐的对于每一个单项进行用*再分隔,从而构造出形如第一次作业的形式,即Hashmap存<指数,系数>,而这样也可以进行狼人优化。
(2)经验
这次作业在强侧中未发现bug,而且在测试开头也没有被狼,但是在结尾被刀了三下,这里的bug就是之前提到的第一次作业中存在的指数中带符号整数的bug(对,没错,这个判断非法性我是直接复制的,所以依然忘了判断,awsl)。
作业到第二次的时候,对java语言的一些好用的性质已经有了了解,虽然使用的还不纯熟,但是依然得到了一些帮助,比如对于连续的加减号,知道了可以直接用ReplaceAll替换为单一加减号,大大减少了处理的困难。
三、第三次作业
(1)实现
被绝望笼罩的人们终于发现,他们来到了魔王的面前。
加入了嵌套的表达式是真的吓死个人,花了十个小时才勉强AC,之后进行减少bug的处理又花去了大量时间,甚至连优化都没有做,说到底还是自己太菜了。
由于java的正则表达式不支持递归处理,所以着实难住了我(不过也因为这个,我才能将正则表达式使用成比较精简的形式,也即课程组希望我们使用的方式)。
经过同学提点,我才意识到一个简易的栈应用,即遇到左括号将count++,遇到右括号将count--,那么当count>0时,一定在括号中,所以将+-*均替换成其它符号,以便通过如第二次作业一样的分隔方式,将每一项分开,然后再将每一个因子分开。但是本次作业与上次不同的地方是,有基础的表达式因子,也有嵌套类型的,所以自然而然的想到递归求导的方式。那么我就将分好的因子归类,分成常数类,x类,sin类,cos类,嵌套类,其中对于前四个类的处理方式与第二次作业相同。对于最后类需要将最外层括号拆去,然后判断是否合法,再送入递归方法中,形成新的expression,再从本段开头方式处理起。想明白了这点,代码自然就水到渠成,不过遗憾的是本人并未想到合适的化简方法,就无脑嵌套括号,导致了求导出的式子很长,值得再进行一番思考。递归函数结构大致如下:
String create(String expression){ //首先以加减拆项 if (常数项) { derivation(); } else if (x项) { derivation(); } else if (sin项) { derivation(); } else if (cos项) { derivation(); } else{ //此处是乘积项,之后通过乘号将乘积项分隔开,形成如上几种同样的情况,以及嵌套项,对于嵌套项将其最外层括号去掉之后,得到新的表达式叫做subexpression,调用create(subexpression)即可实现递归求导。 } }
(2)经验
本次作业实现的中规中矩,强测完全正确,互测也就被hack了一次(同样,被hack的这个点依然是由于复制不到位,不过并不是之前的bug,是本次作业新加的,wsl),但是比较遗憾的是因为能力有限,没有实现化简操作,所以得到的表达式并不是人读的(还好有sympy)。
总的来说,对于如此复杂的程序,如果尝试化简,很容易就爆灯,炸掉几个强测,为了区区的性能分不到五分,损失了几十分,实在是得不偿失,所以不化简就是最好的化简(不过在之后将自己程序进行化简以提高码力是十分重要的)。
由于使用了大量的for,所以十分担心自己的程序会TLE,或者是因为没化简生成的超长表达式会OLE,那样真的是改都没法改,只能重构某个算法,或者整个工程,以后还是应该仔细考虑如何更好的去实现自己想要的功能。
四、总结性分析
综上所述,前三次的面向对象Java作业,我成功的写成了三次面向过程C作业。究其根本是每天的时间太少,要学的东西太多,而本身又比较懒,不愿意去尝试新的写代码方式,还是要尽力去改正。
之后需要去阅读大佬们的第二三次作业代码,看看优化的神仙们是如何使用继承,接口等Java中的特性的,以此来对下面多线程的作业做一个铺垫。
事实上,阅读代码本应该是在互测阶段就完成的事情,但是因为还有其他课要学,迫不得已写了自动评测脚本,成功利用OO训练了OS技巧,嗯,不错。
接下来是对于自己代码之间类依赖的分析,但是由于本人在前三次作业中并未掌握OO的精髓,所以写出来的类可以说是十分的少,而大部分代码全部堆砌在某个或者某几个方法中(Poly类有四五百行,而其他类多则一百多行,少则数十行)。
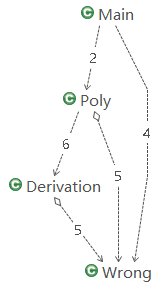
如上图,为第三次作业中(共四个类)之间相互依赖关系,可以看出逻辑十分的简单,比较大的问题是没有体现出原本思考出的逻辑。最初的设计逻辑是读入->分解expression为term->分解term为factor->对每一个factor求导->将所求导递归整合成输出。结果最后将很多功能全部放入了Poly中,Derivation也是完全复制的第二次作业,所以说设计的比较失败。
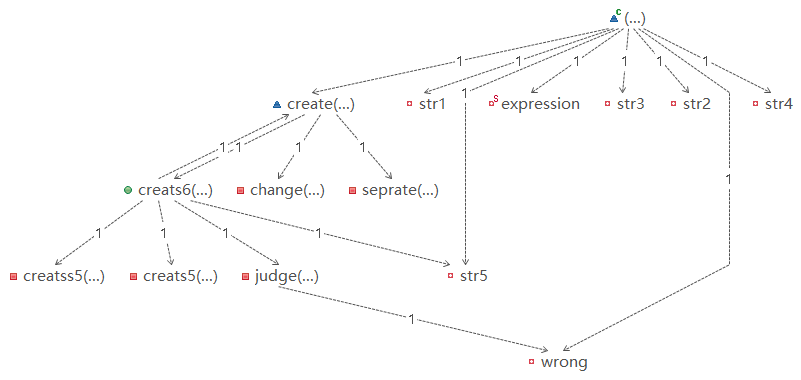
上图为Derivation类,还是能够比较明显的看出求导的结构层次的,所以我认为如果将某些部分,比如说xder,sinder,cosder等整合为一个factor类,以OO的思维来编程,可能会获得更多的好处。
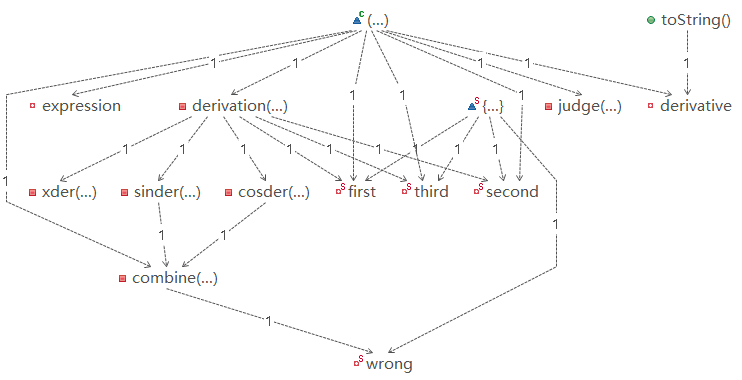
可以说经历过这三次OO作业,有了一些收获,比如说对于自动评测机如何去实现有了一个清晰的认识,对于Java的语法有了一些熟悉等,但是也有很多不足,比如说应该掌握的继承、接口等特性到现在还没完全搞懂,写代码依然是面向过程而无法熟练运用面向对象等。 上图为Poly类,也即处理了几乎全部输入的类,可以看出其中的方法名十分的混乱,因为当时把一大坨代码全放入了create方法中,最后一部分一部分再拆开的,饶是如此,代码看起来依然十分的臃肿不堪,这也提醒了我,或许应该在下次作业中先将作业结构的草图画出来,按照草图去实现自己的代码,可能会更加清晰一些,让自己的思路不那么混乱。
此部分为了节省篇幅,仅将最后一次代码的复杂度贴出,其余两次同理:
| Derivation.combine(String,String) | 4.0 | 6.0 | 6.0 |
| Derivation.cosder(String,String,BigInteger) | 8.0 | 8.0 | 8.0 |
| Derivation.Derivation(String) | 1.0 | 10.0 | 11.0 |
| Derivation.derivation(String,String,String,BigInteger) | 1.0 | 8.0 | 8.0 |
| Derivation.judge(String) | 4.0 | 3.0 | 4.0 |
| Derivation.sinder(String,String,BigInteger) | 11.0 | 11.0 | 11.0 |
| Derivation.toString() | 1.0 | 1.0 | 1.0 |
| Derivation.xder(String,BigInteger) | 4.0 | 4.0 | 4.0 |
| Main.main(String[]) | 1.0 | 2.0 | 2.0 |
| Poly.change(String) | 1.0 | 9.0 | 10.0 |
| Poly.create(String) | 1.0 | 7.0 | 7.0 |
| Poly.creats5(String,String[],String) | 1.0 | 9.0 | 9.0 |
| Poly.creats6(String[]) | 11.0 | 17.0 | 17.0 |
| Poly.creatss5(BigInteger,String[],int) | 1.0 | 9.0 | 10.0 |
| Poly.judge(String,String) | 1.0 | 13.0 | 15.0 |
| Poly.Poly(String) | 1.0 | 1.0 | 1.0 |
| Poly.seprate(String) | 1.0 | 2.0 | 2.0 |
| Wrong.check() | 1.0 | 1.0 | 1.0 |
| Wrong.detect() | 1.0 | 2.0 | 2.0 |
| Wrong.isblank() | 1.0 | 2.0 | 2.0 |
| Wrong.isbracket() | 5.0 | 4.0 | 6.0 |
| Wrong.isnumber() | 1.0 | 1.0 | 1.0 |
| Wrong.issc() | 1.0 | 2.0 | 2.0 |
| Wrong.istrang() | 1.0 | 1.0 | 1.0 |
| Wrong.iswrong() | 1.0 | 1.0 | 1.0 |
| Wrong.otherchar() | 1.0 | 1.0 | 1.0 |
| Wrong.plus() | 1.0 | 3.0 | 3.0 |
| Wrong.Wrong() | 1.0 | 1.0 | 1.0 |
| Wrong.Wrong(String) | 1.0 | 2.0 | 2.0 |
| Total | 69.0 | 141.0 | 149.0 |
| Average | 2.3793103448275863 | 4.862068965517241 | 5.137931034482759 |
五、代码重构分析
最后的最后,需要对作业进行一个brain storm,并且在脑内完成优化流程,以此来减少自己对于面向过程写法的愧疚感。
(1)基础
首先需要整改的当然是各个类之间的关系。
对于输入,仍然可以使用之前的Main类,不再赘述。在将表达式读入之后,先进入Wrong类,判断表达式的基本合法性,再传入Term类,用+-将expression中的每一个项提取出来,同样的,分为Num类,X类,Sin类,Cos类,Mix类。对于除了Mix类之外的几个类,均视为传入了仅含最基本的因子形式(即sin与cos括号内之包含x,且所有类无系数,仅有指数的形式)。对于Mix类可以通过*将其分隔开,传入到新的Factor类中,同时,之前所提到的Num类,X类,Sin类,Cos类,Mix类,依然可以作为Factor中所依赖的类。对于Factor中除Mix之外的类,求导形式均与Term下相同,对于Factor中的Mix类,我们可以知道,它仅含嵌套因子,那么对于此,将其最外层括号除去(若最外层是sin,cos的嵌套同样将sin,cos除去),可以得到一个新的subexpression,将之传入到Term类,即实现了对于表达式的递归处理。对于求导,可以将之作为Num类,X类,Sin类,Cos类的依赖,在每一类中加入Derivation类,同时实现toString方法,将求导后的结果输出为字符串格式,最后经过整合,可以有比较清晰的类关系图。(在处理基本类时,可以通过extends继承实现,不再赘述)
(2)进阶
其次是对于初步化简的处理。
第三次作业化简的难点在于,不清楚形如a*x^b*sin(...)^c*cos(...)^d这样的项中是否含有嵌套,括号的层数也是为止的,所以导致了大多数同学在处理的时候仅仅是无脑加括号,以保证准确性,但是这样做将性能完全的舍弃了。
但是经过如上对类的整合之后,可以很清楚的将层次整理出来,也即,只需要在Factor类返回之后的字符串,与其它同级Factor类字符串相加之后在外层嵌套括号,这样不光减少了输出的长度,而且使得接下来的化简也有迹可循。
对于同一层的Term类,可以通过类来化简,这样可以将最基本的Num类,X类,Sin类,Cos类整合在一起,而单独留下复杂的Mix类。同时,这样的实现也将Mix类中所包含的嵌套项合并了。而在Factor类与Factor类相乘时,需要检查其所属类别,按照Num类,X类,Sin类,Cos类,Mix类来排序,以此来辅助前述的Term类化简(仅需比对字符串是否完全相同即可化简)。
(3)高级
最后是对于神仙化简的一点思考。
在(2)中已经实现了对于同类项的合并,同样的,在同一层完成了对于Term类的遍历之后,可以做的操作有很多,比如将其中的sin^2 + cos^2 = 1化简,最后得到的求导之后的式子呈现出来的形式是化简了sin^2 + cos^2 = 1以及合并同类项等化简的形式。但此时还留有比较长的嵌套项(含有sin^2 + cos^2 = 1这样形式的,但是其中含嵌套的),或者还有简单的,但是可以互相提取公因式的项。由于之前已经对每一个项及每一个因子做了顺序的处理,可以知道,若两项相同,则一定可以通过.equals比对出来。那么对于提取公因式的化简,可以再次对expression进行加减分隔,再用乘分隔,比对一项的每一个因子和其他项的每一个因子是否除了指数部分之外均相同(若缺省则视为指数为1),则可以进行递归提取。
若想对嵌套项进行三角函数合成,则应该在提取公因式之前去做,因为提取公因式之后,本来可以合成的嵌套项可能因此无法较简便的合成,其合成方式与提取公因式相同,不过这里需要比较的是两个不同项其中除sin,cos以外因子是否完全相同,且sin,cos因子具有相同指数,则可以进行提取合成,简化表达式。
六、写在最后
其实,在我看来,这三次作业本身并不在于如何去化简,如何去更好的找出别人的bug,而在于通过阅读别人的代码,来完善自己的代码,同时学到面向对象的精髓,而非因为几个hack就在群里吵的脸红脖子粗。至于性能分,或许真的如助教所说,是为了神仙大佬所准备的,普通人保证了正确性也就很不错了,事实确实是这样,听闻很多人因为优化炸掉了几个点,得不偿失。所以我认为,如果我们没有那个金刚钻,就不要去揽瓷器活,而不如去思考自己代码的架构是否合理,是否真正应用了老师上课所讲的面向对象特性,是否掌握了知识,绝非为了五分性能分而把代码改的面目全非。
愿我们都能在面向对象中习得真谛。
我没有对象,却要面向对象。



