典型的动态规划题目总结（斐波那契数列相关）

1.常规跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

大体思路：

第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达，即走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。所以可以推导出递推公式为：dp[i]=dp[i-1]+dp[i-2]

考虑到 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关，因此可以只用两个变量来存储 dp[i - 1] 和 dp[i - 2]，使得原来的 O(N) 空间复杂度优化为 O(1) 复杂度。具体非递归代码如下：

 

 

 2.变态跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

大致思路：

（1）每一个高度的台阶都可以一步完成，所以每一个位置都有一种基本解 dp[i]=1

(2)除了基本解之外，每一个高度的完成解还受到且仅受到前一个相邻高度dp[i-1]的影响。

（3）因此，每一个高度的最终解都是前一个数的解()+本身的基本解。即，dp[i]=1+dp[i-1];

 3.抢劫一排房子

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

大体思路：

（1）相邻的房间不可以偷==》偷了i就不可以偷i-1.
（2）那么假如i为一排房间的最后一间，那么走过当前i个房间的最大值为：
　　dp[i]=max(dp[i-2]+numms[i],dp[i-1]);
因此，也需要两个值dp[i-1],dp[i-2]。

class Solution {
    public int rob(int[] nums) {
        int pre1=0;
        int pre2=0;
        for(int i=0;i<nums.length;i++){
            int temp=Math.max(nums[i]+pre2,pre1);
            pre2=pre1;
            pre1=temp;
        }
        
        return pre1;
    }
}

4.抢劫一圈房子（环形的第一家和最后一家是相邻的）

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

解题思路：

/**
（1）先考虑直线型的情况，当一共有i个房间时，偷了i,就不能再偷i-1.只能偷i-2.
所以 dp[i]=Math.max(nums[i]+dp[i-2],dp[i-1]);
(2)环形道的话，可以在直线型的基础上进行考虑，因为第一和最后一个变成了相邻，所以
偷了第一个就不能偷最后一个了。
从第二个开始偷，才可以偷最后一个。
因此，可以从这两种路径中选一个最大的作为最终的结果值。
**/

class Solution {
    public int rob(int[] nums) {
        //1.特殊值判断
        if(nums.length==1){
            return nums[0];
        }
//环形解
        int fromOne=maxVal(nums,0,nums.length-2);
        int fromTwo=maxVal(nums,1,nums.length-1);
        return Math.max(fromOne,fromTwo);
    }
    
//直线型解
    private int maxVal(int[]nums,int start,int end){
        int pre1=0;
        int pre2=0;
        for(int i=start;i<=end;i++){
            int temp=Math.max(nums[i]+pre2,pre1);
            pre2=pre1;
            pre1=temp;
        }
        
        return pre1;
    }
}

5.大牛生小牛问题

假设农场中成熟的母牛每年都会生 1 头小母牛，并且永远不会死。第一年有 1 只小母牛，从第二年开始，母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N，求 N 年后牛的数量。

思路：

（1）在前三年，只有母牛才可以生产。

（2）因为所有的牛都不会死，因此，第N-1年的所有牛dp[N-1]都会活到第N年。

  (3)   因为成熟的母牛每年都会生 1 头小母牛。因此，第N-3年中的所有牛到第N年都会新增一个小母牛。dp[N-3]。

N 年后牛的总数量为：一直的大母牛dp[N-1]+新增的小母牛dp[N-3]。

 

 6.矩阵覆盖问题

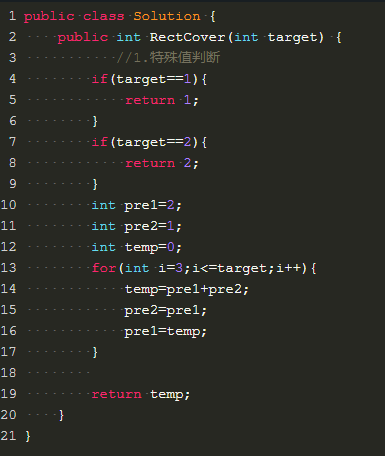
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

思路类似于常规跳台阶。