JPEG图像压缩算法流程详解（转）

 JPEG是Joint Photographic Exports Group的英文缩写，中文称之为联合图像专家小组。该小组隶属于ISO国际标准化组织，主要负责定制静态数字图像的编码方法，即所谓的JPEG算法。JPEG专家组开发了两种基本的压缩算法、两种熵编码方法、四种编码模式。如下所示：

压缩算法：

（1）有损的离散余弦变换DCT（Discrete Cosine Transform）

（2）无损的预测压缩技术；

熵编码方法：

（1）Huffman编码；

（2）算术编码；

编码模式：

（1）基于DCT的顺序模式：编码、解码通过一次扫描完成；

（2）基于DCT的渐进模式：编码、解码需要多次扫描完成，扫描效果由粗到精，逐级递增；

（3）无损模式：基于DPCM，保证解码后完全精确恢复到原图像采样值；

（4）层次模式：图像在多个空间分辨率中进行编码，可以根据需要只对低分辨率数据做解码，放弃高分辨率信息；

       在实际应用中，JPEG图像编码算法使用的大多是离散余弦变换、Huffman编码、顺序编码模式。这样的方式，被人们称为JPEG的基本系统。这里介绍的JPEG编码算法的流程，也是针对基本系统而言。基本系统的JPEG压缩编码算法一共分为11个步骤：颜色模式转换、采样、分块、离散余弦变换（DCT）、Zigzag 扫描排序、量化、DC系数的差分脉冲调制编码、DC系数的中间格式计算、AC系数的游程长度编码、AC系数的中间格式计算、熵编码。下面，将一一介绍这11个步骤的详细原理和计算过程。

 

（1）颜色模式转换

        JPEG采用的是YCrCb颜色空间，而BMP采用的是RGB颜色空间，要想对BMP图片进行压缩，首先需要进行颜色空间的转换。YCrCb颜色空间中，Y代表亮度，Cr,Cb则代表色度和饱和度(也有人将Cb,Cr两者统称为色度)，三者通常以Y,U,V来表示，即用U代表Cb，用V代表Cr。RGB和YCrCb之间的转换关系如下所示：

Y = 0.299R+0.587G+0.114B

Cb = -0.1687R-0.3313G+0.5B+128

Cr = 0.5R=0.418G-0.0813B+128

一般来说，C 值 (包括 Cb Cr) 应该是一个有符号的数字, 但这里通过加上128，使其变为8位的无符号整数，从而方便数据的存储和计算。

R = Y+1.402(Cr-128)

G = Y-0.34414(Cb-128)-0.71414(Cr-128)

B = Y+1.772(Cb-128)

（2）采样

        研究发现，人眼对亮度变换的敏感度要比对色彩变换的敏感度高出很多。因此，我们可以认为Y分量要比Cb,Cr分量重要的多。在BMP图片中，RGB三个分量各采用一个字节进行采样，也就是我们常听到的RGB888的模式；而JPEG图片中，通常采用两种采样方式：YUV411和YUV422，它们所代表的意义是Y,Cb,Cr三个分量的数据取样比例一般是4：1：1或者4：2：2（4：1：1含义就是：在2x2的单元中，本应分别有4个Y，4个U，4个V值，用12个字节进行存储。经过4:1:1采样处理后，每个单元中的值分别有4个Y、1个U、1个V，只要用6个字节就可以存储了）。这样的采样方式，虽然损失了一定的精度但也在人眼不太察觉到的范围内减小了数据的存储量。当然，JPEG格式里面也允许将每个点的U,V值都记录下来；

（3）分块

        由于后面的DCT变换是是对8x8的子块进行处理的，因此，在进行DCT变换之前必须把源图象数据进行分块。源图象中每点的3个分量是交替出现的，先要把这3个分量分开，存放到3张表中去。然后由左及右，由上到下依次读取8x8的子块，存放在长度为64的表中，即可以进行DCT变换。注意，编码时，程序从源数据中读取一个8x8的数据块后，进行DCT变换，量化，编码，然后再读取、处理下一个8*8的数据块。 

JPEG 编码是以每8x8个点为一个单位进行处理的. 所以如果原始图片的长宽不是 8 的倍数, 都需要先补成8的倍数, 使其可以进行一块块的处理。将原始图像数据分为8*8的数据单元矩阵之后，还必须将每个数值减去128，然后一一带入DCT变换公式，即可达到DCT变换的目的。图像的数据值必须减去128，是因为DCT公式所接受的数字范围是-128到127之间。

 

（4）离散余弦变换

        DCT（Discrete Cosine Transform，离散余弦变换），是码率压缩中常用的一种变换编码方法。任何连续的实对称函数的傅里叶变换中只含有余弦项，因此，余弦变换同傅里叶变换一样具有明确的物理意义。DCT是先将整体图像分成N*N的像素块，然后针对N*N的像素块逐一进行DCT操作。需要提醒的是，JPEG的编码过程需要进行正向离散余弦变换，而解码过程则需要反向离散余弦变换。

正向离散余弦变换计算公式：

 

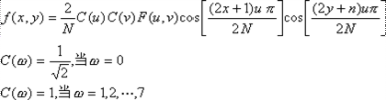
反向离散余弦变换计算公式：

 

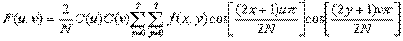
这里的N是水平、垂直方向的像素数目，一般取值为8。8*8的二维像素块经过DCT操作之后，就得到了8*8的变换系数矩阵。这些系数，都有具体的物理含义，例如，U=0，V=0时的F（0,0）是原来的64个数据的均值，相当于直流分量，也有人称之为DC系数或者直流系数。随着U，V的增加，相另外的63个系数则代表了水平空间频率和垂直空间频率分量（高频分量）的大小，多半是一些接近于0的正负浮点数，我们称之为交流系数AC。DCT变换后的8*8的系数矩阵中，低频分量集中在矩阵的左上角。高频成分则集中在右下角。

这里，我们暂时先只考虑水平方向上一行数据（8个像素）的情况时的DCT变换，从而来说明其物理意义。如下图所示：

原始的图像信号（最左边的波形）经过DCT变换之后变成了8个波，其中第一个波为直流成分，其余7个为交流成分。

 

可见图像信号被分解为直流成分和一些从低频到高频的各种余弦成分。而DCT系数只表示了该种成分所占原图像信号的份额大小。显然，恢复图像信息可以表示为下面的式子：

F(n) = C(n)*E(n),这里，E(n)是一个基底，C(n)是DCT系数，F(n)则是图像信号；如果考虑垂直方向的变化，那就需要一个二维的基底。大学里面的信号处理，傅里叶变换等课程上也讲过，任何信号都可以被分解为基波和不同幅度的谐波的组合，而DCT变换的物理意义也正是如此。

由于大多数图像的高频分量比较小，相应的图像高频分量的DCT系数经常接近于0，再加上高频分量中只包含了图像的细微的细节变化信息，而人眼对这种高频成分的失真不太敏感，所以，可以考虑将这一些高频成分予以抛弃，从而降低需要传输的数据量。这样一来，传送DCT变换系数的所需要的编码长度要远远小于传送图像像素的编码长度。到达接收端之后通过反离散余弦变换就可以得到原来的数据，虽然这么做存在一定的失真，但人眼是可接受的，而且对这种微小的变换是不敏感的。

（5）Zigzag扫描排序

         DCT 将一个 8x8 的数组变换成另一个 8x8 的数组. 但是内存里所有数据都是线形存放的, 如果我们一行行的存放这 64 个数字, 每行的结尾的点和下行开始的点就没有什么关系, 所以 JPEG 规定按如下图中的数字顺序依次保存和读取64 个DCT的系数值。

 

这样数列里的相邻点在图片上也是相邻的了。不难发现，这种数据的扫描、保存、读取方式，是从8*8矩阵的左上角开始，按照英文字母Z的形状进行扫描的，一般将其称之为Zigzag扫描排序。如下图所示：

 

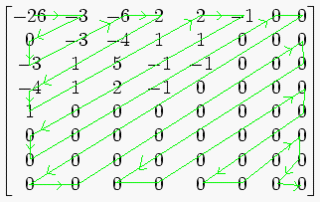
（6）量化

        图像数据转换为DCT频率系数之后，还要进行量化阶段，才能进入编码过程。量化阶段需要两个8*8量化矩阵数据，一个是专门处理亮度的频率系数，另一个则是针对色度的频率系数，将频率系数除以量化矩阵的值之后取整，即完成了量化过程。当频率系数经过量化之后，将频率系数由浮点数转变为整数，这才便于执行最后的编码。不难发现，经过量化阶段之后，所有的数据只保留了整数近似值，也就再度损失了一些数据内容。在JPEG算法中，由于对亮度和色度的精度要求不同，分别对亮度和色度采用不同的量化表。前者细量化，后者粗量化。
    下图给出JPEG的亮度量化表和色度量化表，该量化表是从广泛的实验中得出的。当然，你也可以自定义量化表。

 

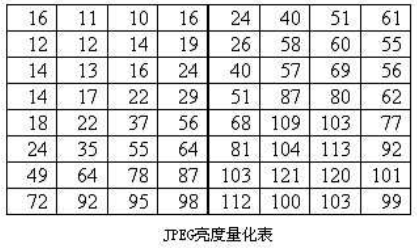
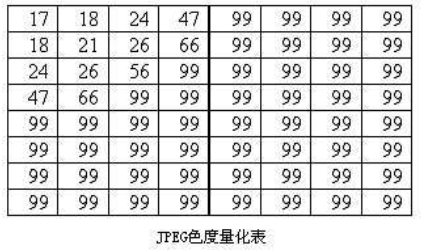
这两张表依据心理视觉阀制作, 对 8bit 的亮度和色度的图象的处理效果不错。量化表是控制 JPEG 压缩比的关键，这个步骤除掉了一些高频量, 损失了很多细节信息。但事实上人眼对高频信号的敏感度远没有低频信号那么敏感。所以处理后的视觉损失很小，从上面的量化表也可以看出，低频部分采用了相对较短的量化步长，而高频部分则采用了相对较长的量化步长，这样做，也是为了在一定程度上得到相对清晰的图像和更高的压缩率。另一个重要原因是所有的图片的点与点之间会有一个色彩过渡的过程，而大量的图象信息被包含在低频率空间中，经过DCT处理后, 在高频率部分, 将出现大量连续的零。

（7）DC系数的差分脉冲调制编码

        8*8的图像块经过DCT变换之后得到的DC系数有两个特点：

（1）系数的数值比较大；

（2）相邻的8*8图像块的DC系数值变化不大；

根据这两个特点，DC系数一般采用差分脉冲调制编码DPCM（Difference Pulse Code Modulation），即：取同一个图像分量中每个DC值与前一个DC值的差值来进行编码。对差值进行编码所需要的位数会比对原值进行编码所需要的位数少了很多。假设某一个8*8图像块的DC系数值为15，而上一个8*8图像块的DC系数为12，则两者之间的差值为3。

（8）DC系数的中间格式计算

        JPEG中为了更进一步节约空间，并不直接保存数据的具体数值，而是将数据按照位数分为16组，保存在表里面。这也就是所谓的变长整数编码VLI。即，第0组中保存的编码位数为0，其编码所代表的数字为0；第1组中保存的编码位数为1，编码所代表的数字为-1或者1......，如下面的表格所示，这里，暂且称其为VLI编码表：

 

前面提到的那个DC差值为3的数据，通过查找VLI可以发现，整数3位于VLI表格的第2组，因此，可以写成（2）（3）的形式，该形式，称之为DC系数的中间格式。

（9）AC系数的行程长度编码(RLC)

        量化之后的AC系数的特点是，63个系数中含有很多值为0的系数。因此，可以采用行程编码RLC（Run Length Coding）来更进一步降低数据的传输量。利用该编码方式，可以将一个字符串中重复出现的连续字符用两个字节来代替，其中，第一个字节代表重复的次数，第二个字节代表被重复的字符串。例如，（4,6）就代表字符串“6666”。但是，在JPEG编码中，RLC的含义就同其原有的意义略有不同。在JPEG编码中，假设RLC编码之后得到了一个（M,N）的数据对，其中M是两个非零AC系数之间连续的0的个数（即，行程长度），N是下一个非零的AC系数的值。采用这样的方式进行表示，是因为AC系数当中有大量的0，而采用Zigzag扫描也会使得AC系数中有很多连续的0的存在，如此一来，便非常适合于用RLC进行编码。

例如，现有一个字符串，如下所示：

57,45,0,0,0,0,23,0,-30,-8,0,0,1,000.....

经过RLC之后，将呈现出以下的形式：

(0,57) ; (0,45) ; (4,23) ; (1,-30) ; (0,-8) ; (2,1) ; (0,0)

注意，如果AC系数之间连续0的个数超过16，则用一个扩展字节(15,0)来表示16连续的0。

（10）AC系数的中间格式

        根据前面提到的VLI表格，对于前面的字符串：

    (0,57) ; (0,45) ; (4,23) ; (1,-30) ; (0,-8) ; (2,1) ; (0,0)

只处理每对数右边的那个数据，对其进行VLI编码: 查找上面的VLI编码表格，可以发现，57在第6组当中，因此，可以将其写成(0,6),57的形式，该形式，称之为AC系数的中间格式。

同样的(0,45)的中间格式为：(0,6),45；

 (1,-30)的中间格式为：(1,5),-30；

 

（11）熵编码

        在得到DC系数的中间格式和AC系数的中间格式之后，为进一步压缩图象数据，有必要对两者进行熵编码。JPEG标准具体规定了两种熵编码方式：Huffman编码和算术编码。JPEG基本系统规定采用Huffman编码（因为不存在专利问题），但JPEG标准并没有限制JPEG算法必须用Huffman编码方式或者算术编码方式。 

Huffman编码：对出现概率大的字符分配字符长度较短的二进制编码，对出现概率小的字符分配字符长度较长的二进制编码，从而使得字符的平均编码长度最短。Huffman编码的原理请参考数据结构中的Huffman树或者最优二叉树。

Huffman编码时DC系数与AC系数分别采用不同的Huffman编码表，对于亮度和色度也采用不同的Huffman编码表。因此，需要4张Huffman编码表才能完成熵编码的工作。具体的Huffman编码采用查表的方式来高效地完成。然而，在JPEG标准中没有定义缺省的Huffman表，用户可以根据实际应用自由选择，也可以使用JPEG标准推荐的Huffman表。或者预先定义一个通用的Huffman表，也可以针对一副特定的图像，在压缩编码前通过搜集其统计特征来计算Huffman表的值。

下面我们举例来说明8*8图像子块经过DCT及量化之后的处理过程：

假设一个图像块经过量化以后得到以下的系数矩阵：

 

15 0 -1 0 0 0 0 0
-2 -1 0 0 0 0 0 0
-1 -1 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0

显然，DC系数为15，假设前一个8*8的图像块的DC系数量化值为12，则当前DC系统同上一个DC系数之间的差值为3，通过查找VLI编码表，可以得到DC系数的中间格式为（2）（3），这里的2代表后面的数字（3）的编码长度为2位；之后，通过Zigzag扫描之后，遇到第一个非0的AC系数为-2，遇到0的个数为1，AC系数经过RLC编码后可表示为（1，-2），通过查找VLI表发现，-2在第2组，因此，该AC系数的中间格式为（1,2）-2；
    其余的点类似，可以求得这个8*8子块熵编码的中间格式为
（DC）（2）（3）；AC（1，2）（-2），（0，1）（-1），（0，1）（-1），（0，1）（-1），（2，1）（-1），（EOB）（0，0）
    对于DC系数的中间格式(2)(3)而言，数字2查DC亮度Huffman表得到011，数字3通过查找VLI编码表得到其被编码为11；
    对于AC系数的中间格式(1,2)(-2)而言，(1,2)查AC亮度Huffman表得到11011，-2通过查找VLI编码表得到其被编码为01；

对于AC系数的中间格式(0,1)(-1)而言，(0,1)查AC亮度Huffman表得到00，数字-1通过查找VLI编码表得到其被编码为0；

对于AC系数的中间格式(2,1)(1)而言，（2,1）查AC亮度Huffman表得到11100，数字-1通过查找VLI编码表得到其被编码为0；

对于AC系数的中间格式(0,0)而言，查AC亮度Huffman表得到1010；
    因此，最后这个8*8子块亮度信息压缩后的数据流为01111，1101101，000，000，000，111000，1010。总共31比特，其压缩比是64*8/31=16.5，大约每个像素用半个比特。