红黑树实现分析
作者:炸鸡可乐
原文出处:www.pzblog.cn
一、故事的起因
JDK1.8最重要的就是引入了红黑树的设计(当冲突的链表长度超过8个的时候),为什么要这样设计呢?好处就是避免在最极端的情况下冲突链表变得很长很长,在查询的时候,效率会非常慢。
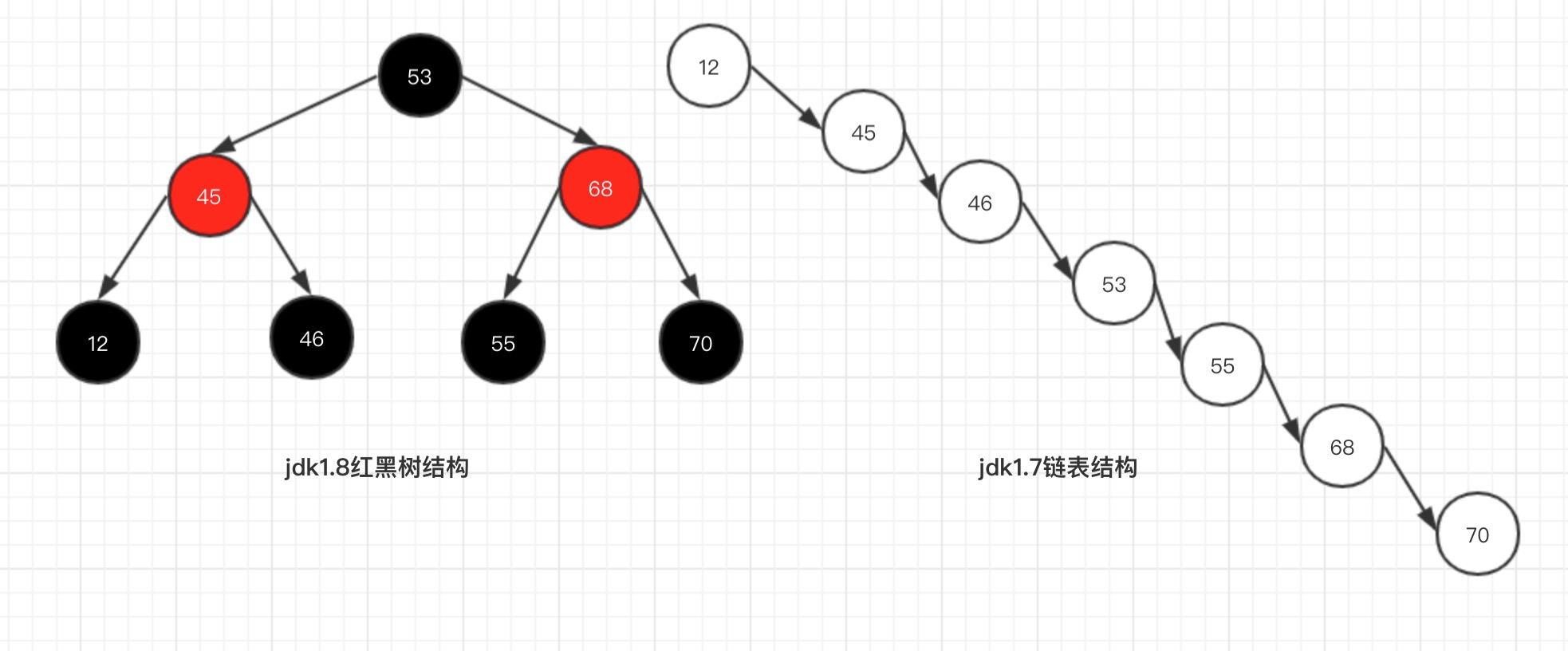
- 红黑树查询:其访问性能近似于折半查找,时间复杂度O(logn);
- 链表查询:这种情况下,需要遍历全部元素才行,时间复杂度O(n);
本文主要是讲解红黑树的实现,只有充分理解了红黑树,对于后面的分析才会更加顺利。
简单的说,红黑树是一种近似平衡的二叉查找树,其主要的优点就是“平衡“,即左右子树高度几乎一致,以此来防止树退化为链表,通过这种方式来保障查找的时间复杂度为log(n)。
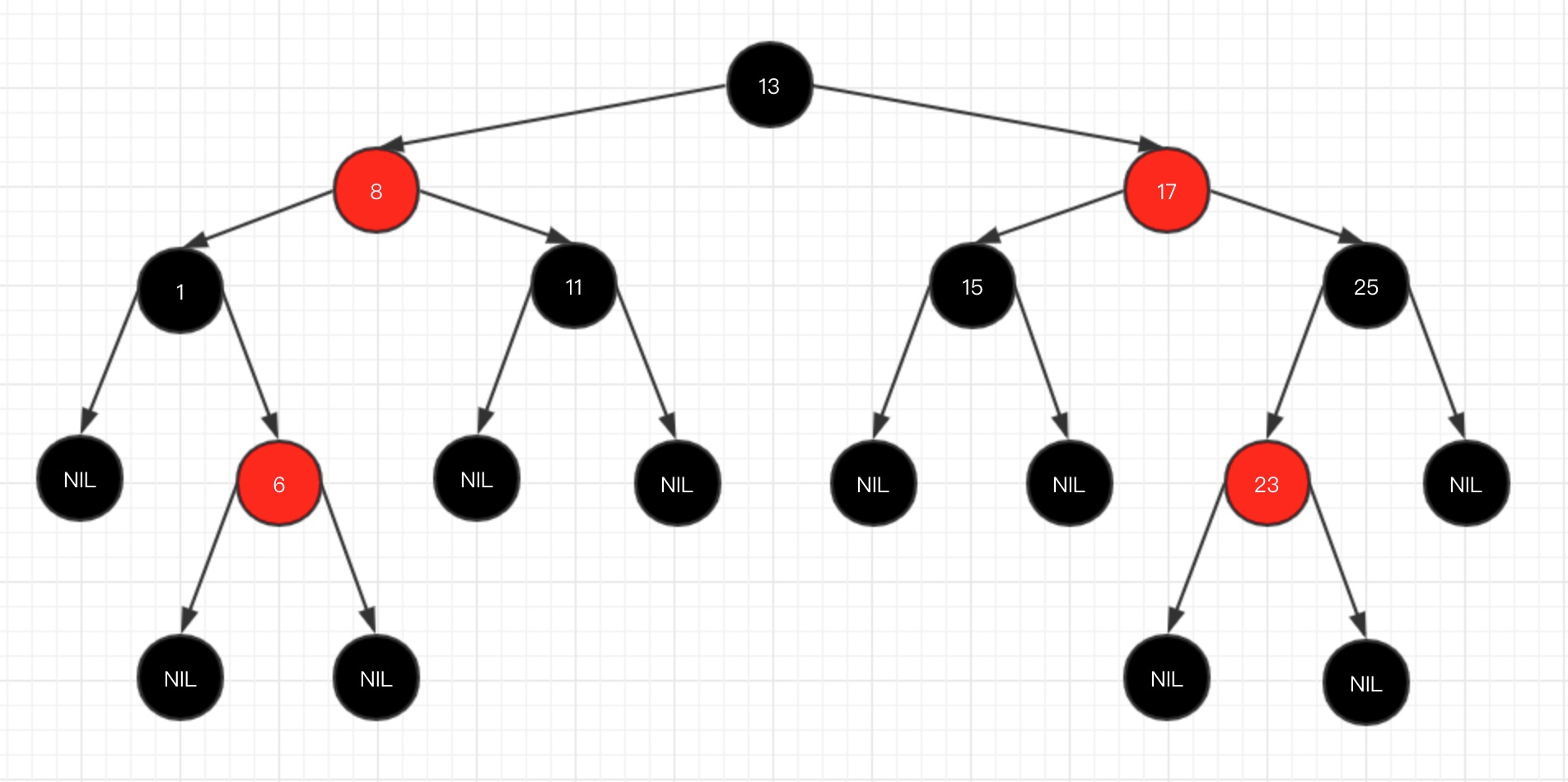
关于红黑树的内容,网上给出的内容非常多,主要有以下几个特性:
- 1、每个节点要么是红色,要么是黑色,但根节点永远是黑色的;
- 2、每个红色节点的两个子节点一定都是黑色;
- 3、红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色);
- 4、从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点;
- 5、所有的叶节点都是是黑色的(注意这里说叶子节点其实是上图中的 NIL 节点);
在树的结构发生改变时(插入或者删除操作),往往会破坏上述条件3或条件4,需要通过调整使得查找树重新满足红黑树的条件。
二、调整方式
上面已经说到当树的结构发生改变时,红黑树的条件可能被破坏,需要通过调整使得查找树重新满足红黑树的条件。
调整可以分为两类:一类是颜色调整,即改变某个节点的颜色,这种比较简单,直接将节点颜色进行转换即可;另一类是结构调整,改变检索树的结构关系。结构调整主要包含两个基本操作:左旋(Rotate Left),右旋(RotateRight)。
2.1、左旋
左旋的过程是将p的右子树绕p逆时针旋转,使得p的右子树成为p的父亲,同时修改相关节点的引用,使左子树的深度加1,右子树的深度减1,通过这种做法来调整树的稳定性。过程如下:
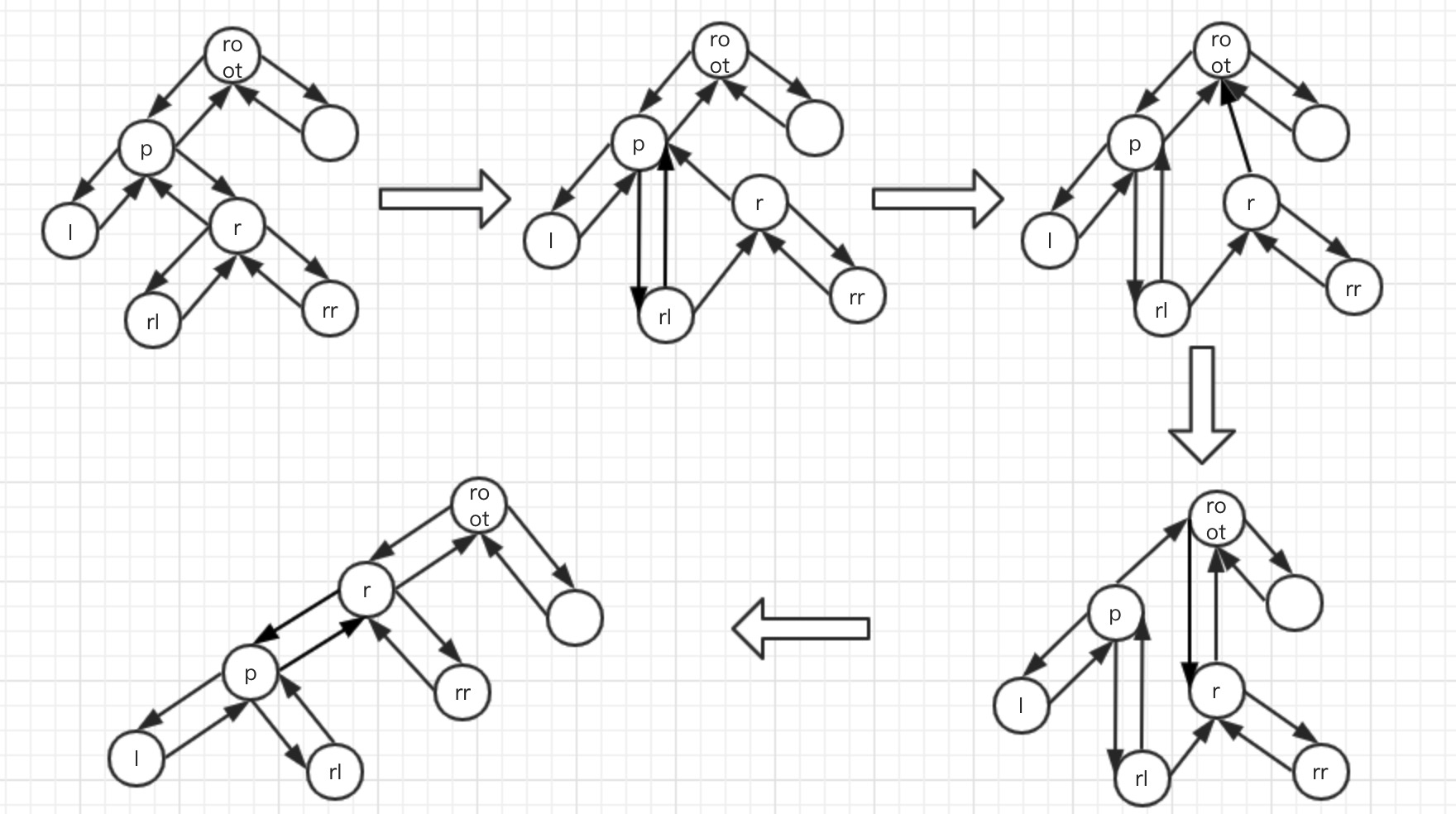
以jdk1.8为例,打开HashMap的源码部分,红黑树内部类TreeNode属性分析:
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
//指向父节点的指针
TreeNode<K,V> parent;
//指向左孩子的指针
TreeNode<K,V> left;
//指向右孩子的指针
TreeNode<K,V> right;
//前驱指针,跟next属性相反的指向
TreeNode<K,V> prev;
//是否为红色节点
boolean red;
......
}
左旋方法rotateLeft如下:
/*
* 左旋逻辑
*/
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
//root:表示根节点
//p:表示要调整的节点
//r:表示p的右节点
//pp:表示p的parent节点
//rl:表示p的右孩子的左孩子节点
TreeNode<K,V> r, pp, rl;
//r判断,如果r为空则旋转没有意义
if (p != null && (r = p.right) != null) {
//多个等号的连接操作从右往左看,设置rl的父亲为p
if ((rl = p.right = r.left) != null)
rl.parent = p;
//判断p的父亲,为空,为根节点,根节点的话就设置为黑色
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
//判断p节点是左儿子还是右儿子
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
2.2、右旋
了解了左旋转之后,相应的就会有右旋,逻辑基本也是一样,只是方向变了。右旋的过程是将p的左子树绕p顺时针旋转,使得p的左子树成为p的父亲,同时修改相关节点的引用,使右子树的深度加1,左子树的深度减1,通过这种做法来调整树的稳定性。实现过程如下:

同样的,右旋方法rotateRight如下:
/*
* 右旋逻辑
*/
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
//root:表示根节点
//p:表示要调整的节点
//l:表示p的左节点
//pp:表示p的parent节点
//lr:表示p的左孩子的右孩子节点
TreeNode<K,V> l, pp, lr;
//l判断,如果l为空则旋转没有意义
if (p != null && (l = p.left) != null) {
//多个等号的连接操作从右往左看,设置lr的父亲为p
if ((lr = p.left = l.right) != null)
lr.parent = p;
//判断p的父亲,为空,为根节点,根节点的话就设置为黑色
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
//判断p节点是右儿子还是左儿子
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
三、操作示例介绍
3.1、插入调整过程图解

3.2、删除调整过程图解
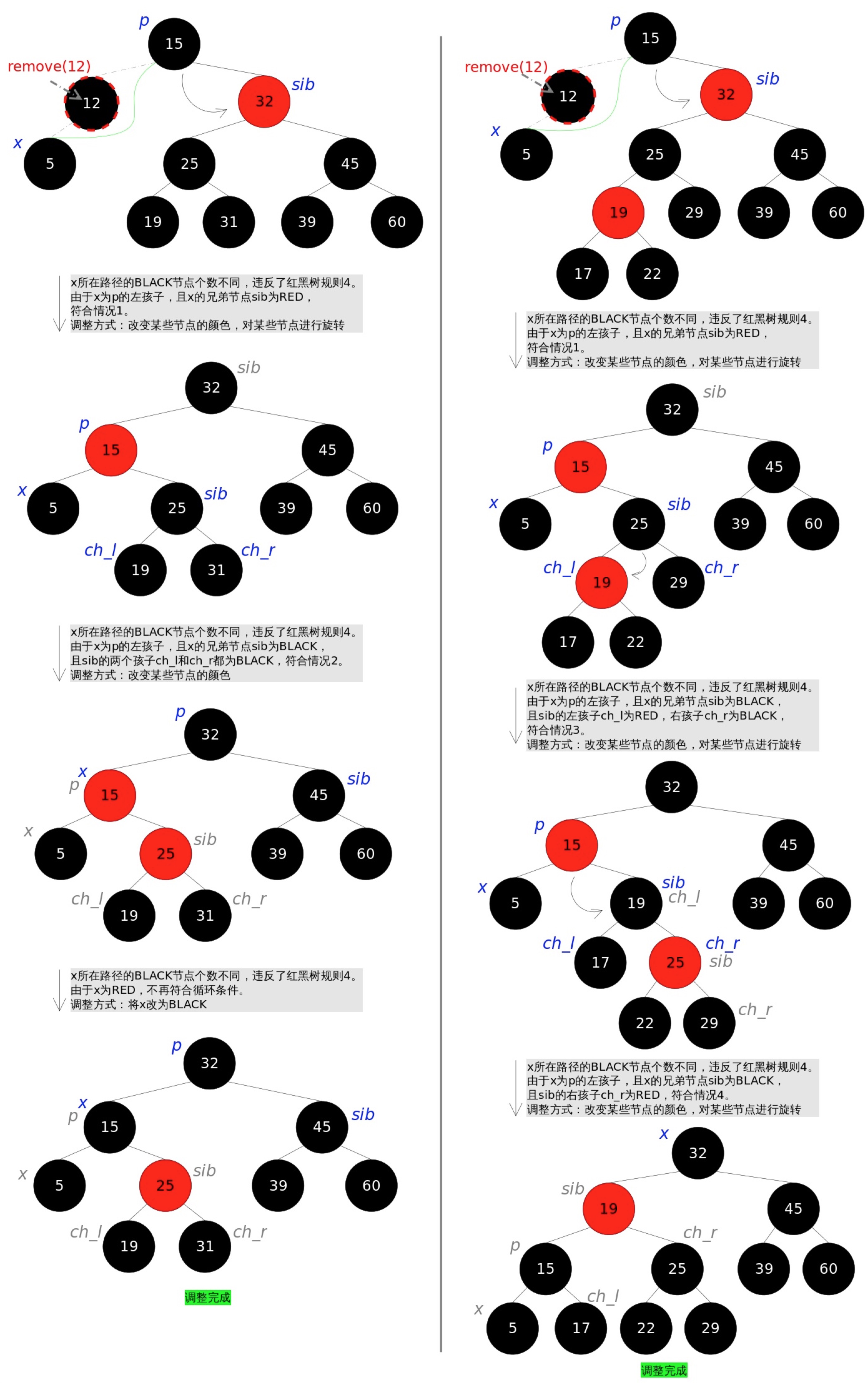
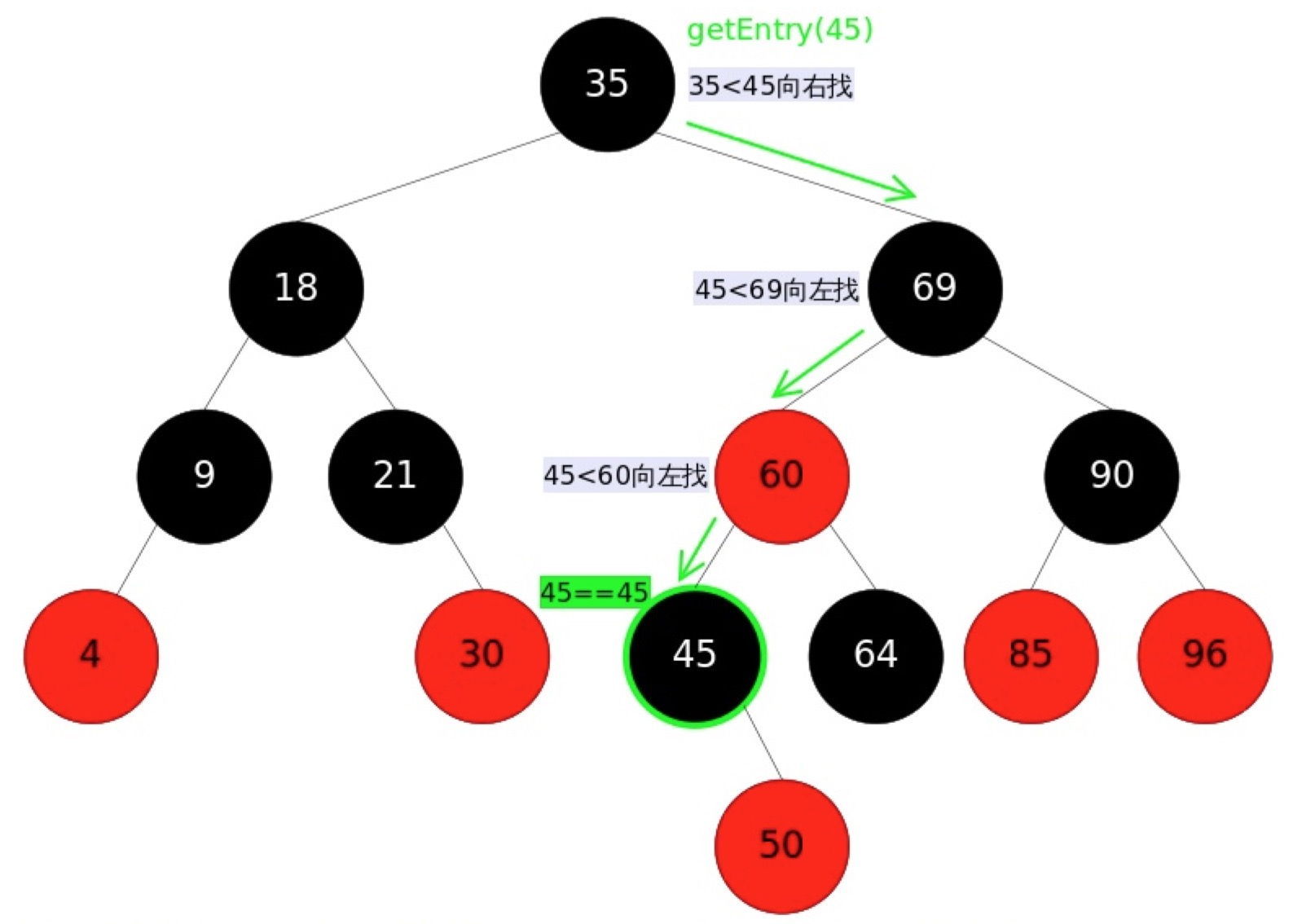
3.3、查询过程图解
四、总结
至此,红黑树的实现就基本完成了,关于红黑树的结构,有很多种情况,情况也比较复杂,但是整体调整流程,基本都是先调整结构然后调整颜色,直到最后满足红黑树特性要求为止。整篇文章,如果有理解不当之处,欢迎指正!



