D44 2-SAT+前缀优化+二分 CF587D Duff in Mafia

视频链接：D44 2-SAT+前缀优化+二分 CF587D Duff in Mafia_哔哩哔哩_bilibili

 

 

 

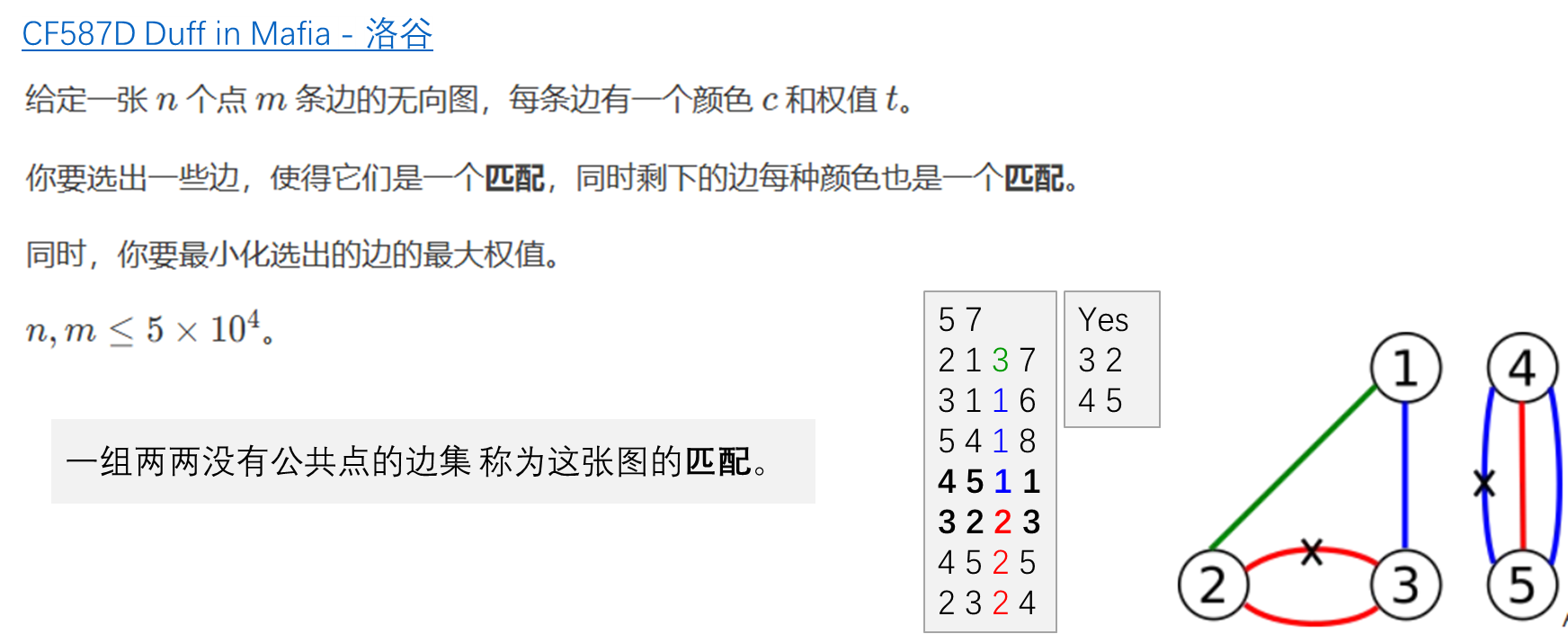
CF587D Duff in Mafia - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;

const int N=500010;
int head[N],idx,ne[N*2],to[N*2];
void add(int x,int y){
  to[++idx]=y;ne[idx]=head[x],head[x]=idx;
}
int dfn[N],low[N],stk[N],scc[N],top,tim,cnt;
int n,m,x0,x1,p0,p1,pp0,pp1,num;
struct E{int x,y,col,val;}e[N]; //读入的边
struct V{int col,id;};
vector<V> v[N]; //端点上的边
bool cmpcol(V x,V y){return x.col<y.col;}

void tarjan(int x){
  dfn[x]=low[x]=++tim;
  stk[++top]=x;
  for(int i=head[x];i;i=ne[i]){
    int y=to[i];
    if(!dfn[y]){ //若y尚未访问
      tarjan(y);
      low[x]=min(low[x],low[y]);
    }
    else if(!scc[y]) //若y已访问且未处理
      low[x]=min(low[x],dfn[y]);
  }
  if(low[x]==dfn[x]){ //若x是SCC的根
    ++cnt;
    for(int y=-1;y!=x;)
      scc[y=stk[top--]]=cnt;
  }
}
bool check(int mid){
  memset(head,0,sizeof(head));
  memset(dfn,0,sizeof(dfn));
  memset(scc,0,sizeof(scc));
  memset(stk,0,sizeof(stk));
  idx=tim=top=cnt=0; num=2*m;
  
  for(int i=1;i<=n;i++){
    // 相同端点的边,选这条则不选其他
    for(int j=0;j<v[i].size();j++){
      x0=v[i][j].id; x1=x0+m;
      p0=++num; p1=++num;
      add(x0,p0); //向下连
      add(p1,x1); //向下连
      if(j!=0){
        add(pp0,p0); //向右连
        add(p1,pp1); //向左连            
        add(pp0,x1); //向右下连
        add(x0,pp1); //向左下连
      }
      pp0=p0,pp1=p1; //前一个节点
    }
    // 剩下的同端点同颜色的边,不选这条则选那条
    for(int j=1;j<v[i].size();j++){
      if(v[i][j-1].col==v[i][j].col){
        add(v[i][j-1].id+m,v[i][j].id);
        add(v[i][j].id+m,v[i][j-1].id);
      }
    }    
  }
  // 边权>mid的边,不选它
  for(int i=1;i<=m;i++) if(e[i].val>mid)add(i,i+m);
  
  for(int i=1;i<=m*2;i++) if(!dfn[i]) tarjan(i);
  for(int i=1;i<=m;i++) if(scc[i]==scc[i+m])return 0;
  return 1;
}
int main(){
  scanf("%d%d",&n,&m);
  for(int i=1;i<=m;i++)
    scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].col,&e[i].val);
  for(int i=1;i<=m;i++){
    v[e[i].x].push_back({e[i].col,i});
    v[e[i].y].push_back({e[i].col,i}); //端点上的边
  }
  for(int i=1;i<=n;i++){
    sort(v[i].begin(),v[i].end(),cmpcol); //按颜色值排序
    for(int j=2;j<v[i].size();j++)
      if(v[i][j-2].col==v[i][j].col) //一个点上超过3条同色边
        return puts("No"),0;
  }
  int l=-1,r=1e9+1,mid; //二分边权
  while(l+1<r){
    mid=(l+r)>>1;
    check(mid)?r=mid:l=mid;
  }
  if(r==1e9+1) return puts("No"),0; //例如三边成环且同色
  check(r);  //退出二分时,检测值可能不是r,故再tarjan一遍
  puts("Yes"); vector<int> v;
  for(int i=1;i<=m;i++) if(scc[i]<scc[i+m])v.push_back(i);
  printf("%d %d\n",r,v.size()); //最小权，匹配边数
  for(int i=0;i<v.size();i++)printf("%d ",v[i]);
}