BZOJ 3259 [Sdoi2014]数表 (莫比乌斯反演 + 树状数组)

3529: [Sdoi2014]数表

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 2321  Solved: 1187
[Submit][Status][Discuss]

Description

    有一张N×m的数表，其第i行第j列（1 < =i < =礼，1 < =j < =m）的数值为
能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。

Input

    输入包含多组数据。
    输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。

Output

    对每组数据，输出一行一个整数，表示答案模2^31的值。

Sample Input

2
4 4 3
10 10 5

Sample Output

20
148

HINT

 

1 < =N．m < =10^5  ， 1 < =Q < =2×10^4

 

Source

Round 1 Day 1

 

析：令F(i) 表示 i 的约数和，这个可以先预处理出来，然后先考虑没有 a 这个限制，令 g(i) 表示gcd(x,y)=i 数对(x,y)的个数，当然1<=x<=n,1<=y<=m，由莫比乌斯反演很容易就可以得到这个式子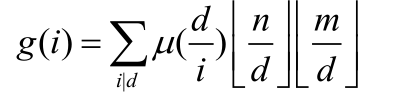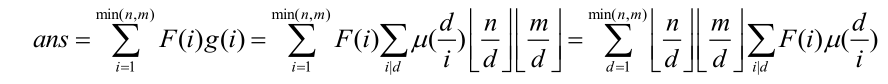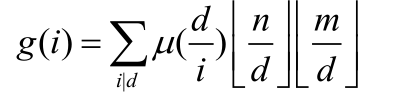然后就能够得到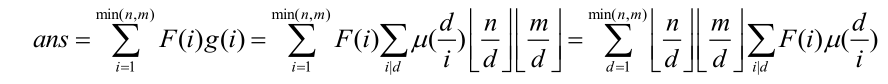

枚举每一个i，暴力更新i的倍数，然后处理前缀和，这样做是O(nlogn)的，有的a的限制，我们可以先把所有的处理都离线，然后将询问按照a排序，i按照F(i)排序，每次询问将所有F(i)<=a的i按照之前的方式插入 用树状数组维护前缀和即可，最后关于取模，这是一个比较特殊的，可以用自然溢出，然后最后答案进行按位与操作也就是ans&2147483647。

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
//#define all 1,n,1
#define FOR(i,x,n)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 1e5 + 5;
const int maxm = 2e4 + 10;
const LL mod = 1e9 + 7LL;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}

bool vis[maxn];
int prime[maxn];
int mu[maxn];

void Moblus(){
  mu[1] = 1;
  int tot = 0;
  for(int i = 2; i < maxn; ++i){
    if(!vis[i])  prime[tot++] = i, mu[i] = -1;
    for(int j = 0; j < tot && i * prime[j] < maxn; ++j){
      int t = i * prime[j];
      vis[t] = 1;
      if(i % prime[j] == 0) break;
      mu[t] = -mu[i];
    }
  }
}

struct Node{
  int val, id;
  bool operator < (const Node &p) const{
    return val < p.val;
  }
};
Node f[maxn];
struct Query{
  int id, n, m, a;
  bool operator < (const Query &q) const{
    return a < q.a;
  }
};
Query q[maxm];


void init(){
  for(int i = 1; i < maxn; ++i){
    f[i].id = i;
    for(int j = i; j < maxn; j += i)
      f[j].val += i;
  }
  sort(f+1, f + maxn);
}

int sum[maxn];

void add(int x, int val){
  while(x < maxn){
    sum[x] += val;
    x += lowbit(x);
  }
}

int query(int x){
  int ans = 0;
  while(x){
    ans += sum[x];
    x -= lowbit(x);
  }
  return ans;
}

int ans[maxn];

int solve(int n, int m){
  if(n > m)  swap(n, m);
  int ans = 0;
  for(int i = 1, det; i <= n; i = det + 1){
    det = min(n/(n/i), m/(m/i));
    ans += (query(det) - query(i-1)) * (n/i) * (m/i);
  }
  return ans & 2147483647;
}

void update(int x, int val){
  for(int i = x, j = 1; i < maxn; i += x, ++j)
    add(i, mu[j] * val);
}


int main(){
  Moblus();
  init();
  int T;  scanf("%d", &T);
  for(int i = 0; i < T; ++i){
    scanf("%d %d %d", &q[i].n, &q[i].m, &q[i].a);
    q[i].id = i;
  }
  sort(q, q + T);
  int j = 1;
  for(int i = 0; i < T; ++i){
    while(f[j].val <= q[i].a)  update(f[j].id, f[j].val), ++j;
    ans[q[i].id] = solve(q[i].n, q[i].m);
  }
  for(int i = 0; i < T; ++i)  printf("%d\n", ans[i]);
  return 0;
}