HDU 5015 233 Matrix (矩阵快速幂)

题意： 有一种矩阵，它的第一行是这样一些数：a  _0,0 = 0, a _0,1 = 233,a _0,2 = 2333,a _0,3 = 23333...) 除此之外，在这个矩阵里, 我们有 a _i,j = a _i-1,j +a _i,j-1( i,j ≠ 0).现在给你 a _1,0,a _2,0,...,a _n,0,求a _n,m 是多少。

析：把这个矩阵构造成n+2 * n+2 的

矩阵快速幂，构造出矩阵即可。

第一列元素为：

0

a1

a2

a3

a4

转化为：

23

a1

a2

a3

a4

3

则第二列为：

23*10+3

23*10+3+a1

23*10+3+a1+a2

23*10+3+a1+a2+a3

23*10+3+a1+a2+a3+a4

3

 

就形成了矩阵：

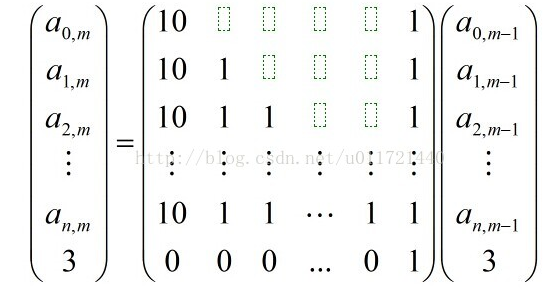
代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#define debug() puts("++++");
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 0x3f3f3f3f3f3f;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 20 + 10;
const int mod = 10000007;
const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, 1, 0, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c){
  return r >= 0 && r < n && c >= 0 && c < m;
}

struct Matrix{
  int a[12][12];
  Matrix(){ memset(a, 0, sizeof a);  }
  void init(){
    for(int i = 0; i < n; ++i)
      a[i][i] = 1;
  }
  friend Matrix operator * (const Matrix &lhs, const Matrix &rhs){
    Matrix res;
    for(int i = 0; i < n; ++i)
      for(int j = 0; j < n; ++j)
        for(int k = 0; k < n; ++k)
          res.a[i][j] = (lhs.a[i][k] * (LL)rhs.a[k][j] + res.a[i][j]) %  mod;
    return res;
  }
};


Matrix fast_pow(Matrix a, int n){
  Matrix res;
  res.init();
  while(n){
    if(n & 1)  res = res * a;
    n >>= 1;
    a = a * a;
  }
  return res;
}


int main(){
  while(scanf("%d %d", &n, &m) == 2){
    Matrix first;
    first.a[0][0] = 23;
    for(int i = 1; i <= n; ++i){
      scanf("%d", &first.a[i][0]);
      first.a[i][0] %= mod;
    }
    first.a[n+1][0] = 3;
    n += 2;
    Matrix second;
    for(int i = 0; i + 1 < n; ++i){
      second.a[i][0] = 10;
      for(int j = 0; j < i; ++j)
        second.a[i][j+1] = 1;
      second.a[i][n-1] = 1;
    }
    second.a[n-1][n-1] = 1;
    Matrix ans = fast_pow(second, m) * first;
    printf("%d\n", ans.a[n-2][0]);
  }
  return 0;
}