【数论】基础数论
基础数论
素数
Eratosthenes 筛法
bool isp[maxn];
void shai() {
isp[1] = 0; for (int i = 2; i <= n; ++i) isp[i] = 1;
for (int i = 2; i * i <= n; ++i) {
if (!isp[i]) continue ;
for (int j = 2 * i; j <= n; j += i) isp[j] = 0;
}
}
欧拉筛 O(n)
int pri[maxn]; bool isp[maxn];
void shai() {
int c1 = 0;
for (int i = 2; i <= n; ++i) {
if (!isp[i]) pri[++c1] = i;
for (int j = 1; j <= c1 && i * pri[j] <= n; ++j) {
isp[i * pri[j]] = 1;
if (i % pri[j] == 0) break;
}
}
}
由于欧拉筛的每个数都是由它的最小质因子筛掉的,所以欧拉筛可以用来预处理每个数的最小质因子。
性质:每个数的质因子最多有 \(O(log)\) 个
证明:就算全都是 \(2\),也只有 \(O(log)\) 个
费马二平方定理
素数 p 在模 4 意义下有 3 种情况
- \(p = 2\)
- \(p\equiv 1(mod~4)\)
- \(p\equiv 3(mod~4)\)
其中 \(p=2\) 和 \(p\equiv 1(mod~4)\) 的 \(p\) 总可以表示成整数 \(x^2+y^2\),且这种表示是唯一的
Gcd
定理 1:\(gcd(a,b)\) 是 \(a\) 和 \(b\) 的线性组合中最小的正整数
证明:令 \(g=gcd(a,b)\),\(s\) 为 \(a\) 和 \(b\) 的线性组合中最小的正整数
\(g|a,g|b\),所以 \(g|(ax+by)\),所以 \(g|s\),又因为 \(g>0,s>0\),所以 \(g\le s\)
令 \(q=\lfloor\frac{a}{s}\rfloor\),我们得到 \(r=a\bmod s=a-qs=a-q(ax+by)=a(1-qx)+b(-qy)\)
也就是说 \(r\) 也是 \(a\) 和 \(b\) 的一个线性组合,由于 \(0\le r<s\),所以 \(r=0\),所以有 \(s|a\),同理有 \(s|b\)
所以 \(s|g\),又因为 \(s>0,g>0\),所以 \(s\le g\)
综上可得 \(s=g\)
定理 2:\(gcd(ax, bx) = xgcd(a, b)\)
证明:显然
定理 3:\(gcd(a, b) = gcd(a - b, b)\)
证明:
定理 4:$gcd(a, b) = gcd(b,a \bmod b) $
证明:
定理 5:\(gcd(a, b) \times lcm(a, b) = ab\)
证明:
令 \(g=gcd(a,b),l=lcm(a,b),a=xg,b=yg\)
\(lcm(a,b)=lcm(xg,yg)=glcm(x,y)=gxy\Rightarrow gcd(a,b)*lcm(a,b)=gxgy=ab\)
定理 6:\(gcd(a^n-1,a^m-1)=a^{gcd(n,m)}-1\)
证明:
\((a^n-1,a^m-1)=(a^n-a^m,a^m-1)=(a^m(a^{n-m}-1),a^m-1)\)
显然 \(a^m\) 和 \(a^m-1\) 互质
所以我们得到 \((a^{n-m}-1,a^m-1)\),也就是说我们可以对指数做辗转相除
所以最后一定能得到 \(a^{(n,m)}-1\)
定理 7:\(lcm(a_1,a_2,...a_n)=\frac{1元gcd之积*3元gcd之积...}{2元gcd之积*4元gcd之积...}\)
首先 \(lcm\) 肯定可以对于每个素因子单独考虑
我们现在仅考虑素数 \(p_i\),不妨设 \(b_i\) 为 \(a_i\) 素因子分解之后 \(p_i\) 的指数
注意到 \(p\) 的贡献为 \(max(b_1,b_2,\cdots,b_n)\)
这个 \(max\) 可以看做是全集的 \(max\),那么我们直接套 \(max-min\) 容斥,就能得到上述式子
欧几里得算法
void gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
复杂度 \(O(\log n)\)
证明:
用 \(a_0\) 和 \(a_1\) 表示初始的两个数。
数列 \(a_i = a_{i-2}~\%~a_{i-1}\) 直到 \(a_k = 0\),最大公约数即为 \(a_{k-1}\)
可以发现 \(a_i\leq a_{i-2} / 2\),也就是说,每两个数减小至少一半,所以复杂度是 \(O(lon)\)
证明:
分情况讨论:
若 \(a_{i-1}\leq a_{i-2}/2\) ,则 \(a_{i}\leq a_{i-2} / 2\)
否则 \(a_{i-1}>a_{i-2} / 2\),则 \(a_{i} = a_{i-2}-a_{i-1}\),则 \(a_i\leq a_{i-2} / 2\)
扩展欧几里得算法 ExGcd
\(ax+by=(a,b)\) 利用扩展欧几里得算法可以找出一对满足条件的整数x,y。当然,这一对x,y是不唯一的。
void exgcd(int a, int b, int &d, int &x, int &y){
if(!b){d = a; x = 1; y = 0;}
else{
exgcd(b, a % b, d, y, x);
y -= x * (a / b);
}
}
证明 : \(ax+by=(a,b)\)
利用 \((a,b)=(b,a\%b)\) 可以不断递归,到底层 \(b = 0\) 则可解出 x 和 y
约数和公式
\(n = p_1^{a_1}*p_2^{a_2}*p_3^{a_3}*...*p_m^{a_m}\)
n 的所有约数的和为 \((1 + p_1+p_1^2+p_1^3+...+p_1^{a_1})(1 + p_2+p_2^2+p_2^3+...+p_2^{a_2})...(1 + p_m+p_m^2+p_m^3+...+p_m^{a_m})\)
考虑到每个括号中都是一个级数(大概吧),然后就能化简成
\(\prod_{i=1}^{m}\frac{p_i^{(a_i+1)}-1}{p_i-1}\) 是不是很神奇
证明:感性理解一下,这个乘法类似于组合数学中整数拆分的思想======= 自己yy 关于下面的哪个级数。
令 \(S(n)=1+ax+ax^2+ax^3+...+ax^n=\sum_{i=0}^{n}ax^i \Rightarrow xS(n)=\sum_{i=1}^{n+1}ax^i \Rightarrow S(n)=\frac{xS(n)-S(n)}{x-1}=\frac{x^{n+1}-1}{x-1}\)
\(O(\sqrt n) 求所有约数\)
for(int i = 1; i * i <= x; ++i){
if(x % i == 0){
//i 是一个约数
if(x != i * i) // x / i 是一个约数
}
}
裴蜀定理
对于整数 \(a,b\) 以及其最大公因数 \(d\),一定有整数 \(x,y\),使得 \(ax + by = d\)
对于不定方程 \(ax+by=c\) 有整数解的充要条件是 \(gcd(a,b)|c\)
证明:令 \(g= gcd(a,b )\)
充分性: 已知 \(g|c\)
\(g\) 是 \(a\) 和 \(b\) 线性组合,证完了
必要性:已知 \(ax+by=c\) 有整数解
所以 \(c\) 是 \(a\) 和 \(b\) 的线性组合
所以 \(g|c\)
在模意义下,可以使得 \(x\) 和 \(y\) 为正整数 ????
裴蜀定理可拓展的到多个数
求 \(\sum_{i|n}\sum_{j|n}[gcd(i,j)=1]\)
一种显然得方法是枚举 n 的约数,复杂度 \(O(n)\),考虑优化
\(n=\prod_{i=1}^mp_i^{a_i}\)
\(\sum_{i_1|p_1^{a_1}}...\sum_{i_m|p_m^{a_m}}\sum_{j_1|p_1^{a_1}}...\sum_{j_m|p_m^{a_m}}[gcd(i_1*...*i_m,j1*...*j_m)=1]\)
\(\sum_{i_1|p_1^{a_1}}...\sum_{i_m|p_m^{a_m}}\sum_{j_1|p_1^{a_1}}...\sum_{j_m|p_m^{a_m}}[gcd(i_1,j_1)=1]*[gcd(i2,j2)=1]*...*[gcd(i_m,j_m)=1]\)
\(\sum_{i_1=0}^{a_1}\sum_{j_1=0}^{a_1}[min(i_1,j_1)=0]...\sum_{i_m=0}^{a_m}\sum_{j_m=0}^{a_m}[min(i_m,j_m)=0]\)
对于 \(\sum_{i=0}^a\sum_{j=0}^a[min(i,j)=0]=2a+1\)
则 \(Ans=\prod_{i=1}^m2a_i+1\)
模
定义:集合 \(S\) 为一个模,仅当 \(S\subseteq Z\),且 \(S\) 满足对加减法封闭,即 \(\forall m,n \in S,m\pm n \in S\)
生成模::集合 \(T\) 的生成模是,最小的模 \(S\) ,使得 \(T\subseteq S\)
实际意义:若 $a\in T,b\in T,a+b\notin TORa-b\notin T $,将 \(a+b,a-b\) 加入 \(T\) 。不断进行。
定理:集合 \(S\) 为一个非零模,当且仅当 \(S\) 中的所有元素都是一个正整数的倍数。
证明:设 \(d\) 是 \(S\) 中的最小正整数。假设存在一个整数 \(x\),\(x\) 不是 \(d\) 的倍数。则 \(x\%d\ne0,且x \%d < d\),故 \(x\%d\) 是 \(S\) 中的最小正整数,与 \(d\) 是 \(S\) 中的最小正整数矛盾
定理:\(gcd(a,b)\) 是 a 和 b 的生成模 \(S\) 中最小正整数。
证明:
设 d 是 \(S\) 中的最小正整数,\(gcd(a,b) \in S\),故 \(d~|~gcd(a,b)\),即 \(d\leq gcd(a,b)\)
\(d\in S\),所以 \(d\) 是 \(a\) 和 \(b\) 线性组合,所以 \(gcd(a,b) ~|~d\),即 \(gcd(a,b) \leq d\)
所以 \(d=gcd(a,b)\)
同余和取模
先看三个公式:(a+b) mod m = ((a mod m) + (b mod m))mod m
(a-b) mod m = ((a mod m) - (b mod m) + m)mod m
ab mod m = (a mod m)(b mod m)mod m
同余的性质
- 自反性:\(a\equiv a(\bmod m)\)
- 对称性:若 \(a\equiv b(\bmod m)\),则 \(b\equiv a(\bmod m)\)
- 同加性:若 \(a\equiv b(\bmod m)\),则 \(a+c\equiv b+c(\bmod m)\)
- 同减性:若 \(a\equiv b(\bmod m)\),则 \(a-c\equiv b-c(\bmod m)\)
- 同乘性:若 \(a\equiv b(\bmod m)\),则 \(ac\equiv bc(\bmod m)\)
- 同幂性:若 \(a\equiv b(\bmod m)\),则 \(a^n\equiv b^n(\bmod m)\)
- 推论1:若 \(a\bmod p=k\),\(a\bmod q=k\),且 \(gcd(p,q)=1\),则 \(a\bmod pq=k\)
- 注意:同余不满足同除性,即 a $$\div$$ n $$\not\equiv$$ b $$\div$$ n (mod m)
幂取模
求 \(a^n\bmod p\)
思路:在快速幂的过程中取模
ll pow_mod(ll x, ll n) {
ll s = 1;
for(; n; n >>= 1) {
if(n & 1) s = s * x % p;
x = x * x % p;
} return s;
}
对于同余方程 \(ax\equiv d(mod~m)\),\(m\) 为质数,d = \(gcd(a,m)\)
\(ax\equiv d(mod~m)\Rightarrow ax+my=d\) 利用 \(exgcd\) 算法可以求得一组解,但要是于要求是最小正整数解。
考虑 \(ax+my=d\),令 \(x=x-m,y=y+a\),\(ax+by\) 依然 \(=d\),且 \(x\) 变小了,只告诉我们 \(x\) 可以对 \(m\) 取模。
但是可不可以更小。考虑令 \(x=x-m,y=y+a\),也可以让 \(x=x-m/d,y=y+a/d\),也就是说 \(x\) 可以对 \(m/d\) 取模
BSGS
用于求解 \(a^x\equiv y(mod~p)\) \(p\) 是一个素数
令 \(q=\sqrt p\) 考虑最终答案 \(x\) 一定在 \([0,p-1]\)。
在考虑两个数列 \(S=[a^0,a^1,...,a^q],T=[a^0,a^q,a^{2q}...,a^{q^2}]\)
对于任意的 x,都可以用 \(t_1\in S,t_2 \in T\) 表示,即 \(a^x\equiv a^{t_1+t_2}\equiv y \Rightarrow a^{t_2}\equiv y*{a^{t_1}}^{-1}\)
将 \(t_2\) 放到 hash 表里,枚举 \(t_1\),查表即可。时间复杂度 \(O(\sqrt n)\)
对于 p 不是素数的情况,可以用 exBSGS
拓展欧拉定理
\(\begin{equation}~a^c~\equiv~\left\{ \begin{array}\\ a^{c~Mod~\phi(m)} &\gcd(a,m)~=~1 \\ a^c &\gcd(a,m)~\neq~1~\and~c~<~\phi(m) \\ a^{c~Mod~\phi(m)~+~\phi(m)} & \gcd(a,m)~\neq~1~\and~c~\geq~\phi(m) \end{array} \right. \end{equation}\)
逆元
概念:对于正整数 $a $ 和 \(m\),如果有 \(ax\equiv 1\mod(m)\),并且 \(gcd(a,m)=1\),则把这个同余方程中 \(x\) 的最小正整数解叫做 $ a \bmod(m)$ 的逆元
作用:在求解除法取模问题 \((a/b)\%m\) 时,我们发现除法不能直接取模,解决方法就是用乘法逆元,除以一个数取模等于乘以这个数的逆元再取模,即a/b=(a * inv(b))%m
证明:\(\frac{a}{b}\equiv k\mod(m)\Rightarrow \frac{a}{b*b^{-1}}\equiv \frac{k}{b^{-1}}\mod(m) \Rightarrow a\equiv\frac{k}{b^{-1}}\mod(m)\Rightarrow a*b^{-1}\equiv k\mod(m)\)
当然对于 \((a/b)\%m\),还可将其转换为 \((a\%bm)/b\)
证明:令 \((a/b)\%m=x\),则 \(a/b=km+x\Rightarrow a=kmb+bx\Rightarrow a\%bm=bx\Rightarrow(a\%bm)/b=x\)
求法:
1.费马小定理
要求:p 为素数,然后求 $$a^{p-2}~mod ~p$$
2.扩展欧几里得
要求:gcd(a,m)=1,ax $$\equiv$$ 1(mod m)可以转换为ax-my=1,把y写成+的形式就是ax+my=1,因为a与m互素,所以可以直接套用扩展欧几里得求出x即可
代码:
int inv(int a,int m){//计算a在模m下的逆
int d,x,y;
exgcd(a,m,d,x,y);
return d == 1 ? (x+n)%n :-1;
}
3.线性求逆元
求一组数模m的逆元
设 \(m=k*i+r\Rightarrow k*i+r\equiv 0\mod(m)\Rightarrow k+r*i^{-1}\equiv 0 \mod(m)\)
\(\Rightarrow k*r^{-1}+i^{-1}\equiv 0\mod(m)\Rightarrow i^{-1}\equiv-k*r^{-1}\mod(m)\Rightarrow i^{-1}\equiv -m/i*(m\%i)^{-1}\)
另外:1 -> p-1 的所有数的逆元对应了 1 -> p-1 的所有数,既是单射也是满射
#include<iostream>
#include<cstdio>
#define maxn 3000010
#define ll long long
using namespace std;
int n, m;
ll inv[maxn];
int main(){
cin >> n >> m; inv[1] = 1;
for(int i = 2; i <= n; ++i){
inv[i] = -1ll * (m / i) * inv[m % i];
inv[i] = (inv[i] % m + m) % m;
}
for(int i = 1; i <= n; ++i) printf("%lld\n", inv[i]);
return 0;
}
剩余系
完全剩余系
模 \(p\) 意义下的完全剩余系为 \(\{0,1,2,3,...,p-1\}\)
性质:
-
若 \(a_i\) 构成了模 \(p\) 的完全剩余系,\(gcd(m,p)=1\),\(k\in Z\),则 \(k+ma_i\) 也构成模 \(p\) 的完全剩余系
证明:
假设 \(k+ma_i\equiv k+ma_j(mod~p)\)
则 \(ma_i\equiv ma_j(mod~p)\) 两边同乘 \(m\) 在模 \(p\) 意义下的逆元
则 \(a_i\equiv a_j(mod~p)\) 不成立
简化剩余系(缩系)
模 \(p\) 的缩系为 \(\{a_i\}\),\(0<a_i<p\),且 \(gcd(p, a_i)=1\),这样的 \(a_i\) 有 \(\varphi(p)\) 个
性质:
-
若 \(a_i\) 构成了模 \(p\) 的简化剩余系,\(gcd(m,p)=1\),则 \(ma_i\) 也构成模 \(p\) 的完全剩余系
-
如果 \(gcd(p,p')=1\),\(a_i\) 遍历模 \(p\) 的一个缩系,\(a_i'\) 遍历模 \(p'\) 的一个缩系,则 \(a_i*p'+a_i'*p\) 遍历 \(pp'\) 的缩系
证明:
阶
若 \(a\) 、\(p\) 为正整数,且 \(gcd(a,p)=1\),称满足 \(a^r\equiv 1(mod~p)\) 的最小正整数 \(r\) 为 \(a\) 模 \(p\) 的阶(可以写成 \(Ord_p(a)\)
由欧拉定理,\(a^{\varphi(p)}\equiv 1(mod~p)\),所以 \(Ord_p(a)~|~\varphi(p)\)
求阶只能从小到大枚举 ==
原根
若 \(a\) 、\(p\) 为正整数,且 \(gcd(a,p)=1\),称满足 \(Ord_p(a)=\varphi(p)\) 的 \(a\) 为模 \(p\) 的一个原根
关于原根的几个性质
- 注意到所有的素数都有原根
- 当正整数 \(p\) 有原根时,原根的个数为 \(\varphi(\varphi(p))\)
- 令 \(p\) 的原根是 \(g\),那么 \(g,g^2,...,g^{\varphi(p)}\) 构成了模 \(p\) 简化剩余系
求素数原根的方法:
从小到大枚举 \(d,d\in [2,p-1]\),令 $a_i $ 为 \(\varphi(p )\) 的素因子,验证 \(d^{\frac{\varphi(p)}{a_i}}\equiv 1(mod~p)\) 是否都不成立,如果都不成立,那么 d 就是模 \(p\) 的一个原根
这种方法的证明:
假设对于 \(d^{\frac{\varphi(p)}{a_i}}\equiv 1(mod~p)\) 均不成立,但存在 \(k,k<\varphi(p)\),使得 \(d^k\equiv1(mod~p)\)
那么 \(gcd(k,\varphi(p))<p\) 并且 \(gcd(k,\varphi(p))\) 一定整除 \(\frac{\varphi(p)}{a_i}\) 中的一个,不妨设它整除 \(\frac{\varphi(p) }{a_i}\)
考虑在模意义下的等式 \(kx+\varphi(p)y\equiv gcd(k,\varphi(p))~(mod~\varphi(p))\),容易发现一定存在正整数解
我们知道 \(d^{kx+\varphi(p)y}\equiv 1(mod~p)\),所以 \(d^{gcd(k,\varphi(p))}\equiv 1(mod~p)\),而 \(gcd(k,\varphi(p))~|~\frac{\varphi(p)}{a_i}\),这与假设矛盾
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define maxn 500010
#define ll long long
using namespace std;
int p, a[maxn], c1;
ll pow_mod(ll x, ll n) {
ll s = 1;
for (; n; n >>= 1) {
if (n & 1) s = s * x % p;
x = x * x % p;
} return s;
}
int ans;
int main() {
cin >> p; int n = p - 1;
for (int i = 2; i * i <= n; ++i)
if (n % i == 0) {
a[++c1] = i;
while (n % i == 0) n /= i;
}
for (int i = 2; i < p; ++i) {
bool F = 1;
for (int j = 1; j <= c1; ++j)
if (pow_mod(i, (p - 1) / a[j]) == 1) { F = 0; break; }
if (F) { ans = i; break; }
} cout << ans << endl;
return 0;
}
二次剩余
定义:对于整数 \(x,d,p\),如果存在 \(x\),使得 \(x^2\equiv d(mod~p)\),则称 \(d\) 是 \(p\) 的二次剩余
以下讨论的皆是质数的二次剩余,即 \(p\) 是质数。
如何一个数是否是一个二次剩余
\(x^2\equiv a(mod~p)\) 设原根为 \(b,x=b^s,a=b^t\)
\(b^{2s}\equiv b^t(mod~p)\Rightarrow 2s\equiv t(mod~p-1)\)
因为 p - 1 一定是一个偶数,所以如果 \(t\) 为奇数,原式无解
考虑 \(t\) 为偶数的情况,\(1\le s \le p - 1\),所以 \(s_1=t/2,s_2=t/2+(p-1)/2\)
所以 \(x=b^{t/2}\) 或 \(x=b^{t/2}b^{(p-1)/2}=-b^{t-2}\)
以上的算法是在知道原根的情况下,并且复杂度与 \(p\) 同阶,一般没啥用???
考虑别的方法。
勒让德符号
定义: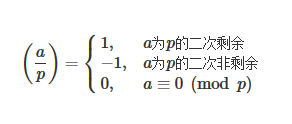
定理:\((\frac{a}{p})\equiv a^{\frac{p-1}{2}}(mod~p)\),方程有解当且仅当 \(a^{\frac{p-1}{2}}\equiv 1(mod~p)\)
证明:
当 \((\frac{a}{p})=1\) 时,方程 \(x^2\equiv a(mod~p)\) 有解,则 \(x\equiv a^{\frac{1}{2}}(mod~p)\)。我们知道 \(x^{p-1}\equiv 1(mod~p)\),所以 \(a^{\frac{p-1}{2}}\equiv 1(mop~p)\)
当 $$
定理:对于质数 p,只有 \(\frac{p-1}{2}\) 个二次剩余
证明:对于 \(1\le u,v\le p-1,u+v=p\),\(p|(u+v)\),则 \(p|(u+v)(u-v)\),则 \(p|(u^2-v^2)\),则 \(u^2\equiv v^2(mod~p)\)
定理:\((a+b)^p\equiv a^p+b^p(mod~p)\)
证明:
\((a+b)^p=\sum_{i=0}^pa^ib^{p-i}C_p^i\)
当 \(i\) 不等于 0 和 p 时,\(C_p^i=\frac{p!}{i!(p-i)!}\) 中的 p 因为是质数,不可能被约掉,所以一定是 p 的倍数





