实验一:决策树算法实验
实验一:决策算法实验
| 20大数据三班 |班级链接|
| ---- | ---- | ---- |
|作业要求|作业链接|
| 学号 | 201613304 |
实验目的
- 理解决策树算法原理,掌握决策树算法框架
- 理解决策树学习算法的特征选择,树的生成和树的剪枝;
- 能根据不同的数据类型,选择不同的决策树算法;
- 针对特定应用场景及数据,能应用决策树算法解决实际问题。
实验内容
- 设计算法实现熵、经验条件熵、信息增益等方法。
- 实现ID3算法。
- 熟悉sklearn库中的决策树算法
- 针对iris数据集、应用skelearn决策树进行类别预测
- 针对iris数据集,利用自编决策树算法进行类别预测。
实验报告要求
- 对照实验内容,撰写实验过程,算法,及测试结果;
- 代码规范化、命名规则、注释;
- 分析核心算法的复杂度;
- 查阅文献、讨论ID3、C4.5算法的应用场景
- 查阅文献、分析决策树剪枝策略。
实验内容及结果
实验代码及截图
- 导入模块所使用的包
点击查看代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from _collections import _count_elements
import math
from math import log
import pprint
- 导入数据
点击查看代码
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况',u'类别'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
点击查看代码
dataSet, features = createDataSet()
trainData = pd.DataFrame(dataSet,columns=features)
print(trainData)
4.采用ID3算法计算信息增益
点击查看代码
def calcShannonEnt(dataSet):
numEntires = len(dataSet) # 返回数据集的行数
labelCounts = {} # 保存每个标签(Label)出现次数的字典
for featVec in dataSet: # 对每组特征向量进行统计
currentLabel = featVec[-1] # 提取标签(Label)信息
if currentLabel not in labelCounts.keys(): # 如果标签(Label)没有放入统计次数的字典,添加进去
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # Label计数
shannonEnt = 0.0 # 经验熵(香农熵)
for key in labelCounts: # 计算香农熵
prob = float(labelCounts[key]) / numEntires # 选择该标签(Label)的概率
shannonEnt -= prob * log(prob, 2) # 利用公式计算
return shannonEnt # 返回经验熵(香农熵)
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 划分数据集的特征
value - 需要返回的特征的值
"""
def splitDataSet(dataSet, axis, value):
retDataSet = [] # 创建返回的数据集列表
for featVec in dataSet: # 遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] # 去掉axis特征
reducedFeatVec.extend(featVec[axis + 1:]) # 将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec)
return retDataSet # 返回划分后的数据集
"""
函数说明:选择最优特征
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
"""
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征数量
baseEntropy = calcShannonEnt(dataSet) # 计算数据集的香农熵
bestInfoGain = 0.0 # 信息增益
bestFeature = -1 # 最优特征的索引值
for i in range(numFeatures): # 遍历所有特征
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # 创建set集合{},元素不可重复
newEntropy = 0.0 # 经验条件熵
for value in uniqueVals: # 计算信息增益
subDataSet = splitDataSet(dataSet, i, value) # subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) # 计算子集的概率
newEntropy += prob * calcShannonEnt(subDataSet) # 根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy # 信息增益
# for j in range(numFeatures):
# print(j)
print("第%d个特征的增益为%.3f" % (i, infoGain)) # 打印每个特征的信息增益
# print(infoGain.dtype)
if (infoGain > bestInfoGain): # 计算信息增益
bestInfoGain = infoGain # 更新信息增益,找到最大的信息增益
bestFeature = i # 记录信息增益最大的特征的索引值
return bestFeature # 返回信息增益最大的特征的索引值
点击查看代码
from math import log
import operator
"""
函数说明:创建测试数据集
"""
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['年龄', '有工作', '有自己的房子', '信贷情况'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet - 数据集
Returns:
shannonEnt - 经验熵(香农熵)
"""
def calcShannonEnt(dataSet):
numEntires = len(dataSet) # 返回数据集的行数
labelCounts = {} # 保存每个标签(Label)出现次数的字典
for featVec in dataSet: # 对每组特征向量进行统计
currentLabel = featVec[-1] # 提取标签(Label)信息
if currentLabel not in labelCounts.keys(): # 如果标签(Label)没有放入统计次数的字典,添加进去
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # Label计数
shannonEnt = 0.0 # 经验熵(香农熵)
for key in labelCounts: # 计算香农熵
prob = float(labelCounts[key]) / numEntires # 选择该标签(Label)的概率
shannonEnt -= prob * log(prob, 2) # 利用公式计算
return shannonEnt # 返回经验熵(香农熵)
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 划分数据集的特征
value - 需要返回的特征的值
"""
def splitDataSet(dataSet, axis, value):
retDataSet = [] # 创建返回的数据集列表
for featVec in dataSet: # 遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] # 去掉axis特征
reducedFeatVec.extend(featVec[axis + 1:]) # 将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec)
return retDataSet # 返回划分后的数据集
"""
函数说明:选择最优特征
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
"""
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征数量
baseEntropy = calcShannonEnt(dataSet) # 计算数据集的香农熵
bestInfoGain = 0.0 # 信息增益
bestFeature = -1 # 最优特征的索引值
for i in range(numFeatures): # 遍历所有特征
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # 创建set集合{},元素不可重复
newEntropy = 0.0 # 经验条件熵
for value in uniqueVals: # 计算信息增益
subDataSet = splitDataSet(dataSet, i, value) # subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) # 计算子集的概率
newEntropy += prob * calcShannonEnt(subDataSet) # 根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy # 信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain)) # 打印每个特征的信息增益
if (infoGain > bestInfoGain): # 计算信息增益
bestInfoGain = infoGain # 更新信息增益,找到最大的信息增益
bestFeature = i # 记录信息增益最大的特征的索引值
return bestFeature # 返回信息增益最大的特征的索引值
"""
函数说明:统计classList中出现此处最多的元素(类标签)
Parameters:
classList - 类标签列表
Returns:
sortedClassCount[0][0] - 出现此处最多的元素(类标签)
"""
def majorityCnt(classList):
classCount = {}
for vote in classList: # 统计classList中每个元素出现的次数
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 根据字典的值降序排序
return sortedClassCount[0][0] # 返回classList中出现次数最多的元素
"""
函数说明:递归构建决策树
Parameters:
dataSet - 训练数据集
labels - 分类属性标签
featLabels - 存储选择的最优特征标签
Returns:
myTree - 决策树
"""
def createTree(dataSet, labels, featLabels):
classList = [example[-1] for example in dataSet] # 取分类标签(是否放贷:yes or no)
if classList.count(classList[0]) == len(classList): # 如果类别完全相同则停止继续划分
return classList[0]
if len(dataSet[0]) == 1: # 遍历完所有特征时返回出现次数最多的类标签
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) # 选择最优特征
bestFeatLabel = labels[bestFeat] # 最优特征的标签
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel: {}} # 根据最优特征的标签生成树
del (labels[bestFeat]) # 删除已经使用特征标签
featValues = [example[bestFeat] for example in dataSet] # 得到训练集中所有最优特征的属性值
uniqueVals = set(featValues) # 去掉重复的属性值
for value in uniqueVals:
subLabels = labels[:]
# 递归调用函数createTree(),遍历特征,创建决策树。
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
return myTree
"""
函数说明:使用决策树执行分类
Parameters:
inputTree - 已经生成的决策树
featLabels - 存储选择的最优特征标签
testVec - 测试数据列表,顺序对应最优特征标签
Returns:
classLabel - 分类结果
"""
def classify(inputTree, featLabels, testVec):
firstStr = next(iter(inputTree)) # 获取决策树结点
secondDict = inputTree[firstStr] # 下一个字典
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else:
classLabel = secondDict[key]
return classLabel
'''
函数说明:获取决策树叶子结点的数目
Parameters:
myTree - 决策树
Returns:
numLeafs - 决策树的叶子结点的数目
'''
def getNumLeafs(myTree):
numLeafs = 0 # 初始化叶子
# python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,
# 可以使用list(myTree.keys())[0]
firstStr = next(iter(myTree))
secondDict = myTree[firstStr] # 获取下一组字典
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
"""
函数说明:获取决策树的层数
Parameters:
myTree - 决策树
Returns:
maxDepth - 决策树的层数
"""
def getTreeDepth(myTree):
maxDepth = 0 # 初始化决策树深度
# python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,
# 可以使用list(myTree.keys())[0]
firstStr = next(iter(myTree))
secondDict = myTree[firstStr] # 获取下一个字典
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth:
maxDepth = thisDepth # 更新层数
return maxDepth
'''
函数说明:绘制结点
Parameters:
nodeTxt - 结点名
centerPt - 文本位置
parentPt - 标注的箭头位置
nodeType - 结点格式
'''
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
arrow_args = dict(arrowstyle="<-") # 定义箭头格式
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14) # 设置中文字体
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', # 绘制结点
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, fontproperties=font)
'''
函数说明:标注有向边属性值
Parameters:
cntrPt、parentPt - 用于计算标注位置
txtString - 标注的内容
'''
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0] # 计算标注位置
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
"""
函数说明:绘制决策树
Parameters:
myTree - 决策树(字典)
parentPt - 标注的内容
nodeTxt - 结点名
"""
def plotTree(myTree, parentPt, nodeTxt):
decisionNode = dict(boxstyle="sawtooth", fc="0.8") # 设置结点格式
leafNode = dict(boxstyle="round4", fc="0.8") # 设置叶结点格式
numLeafs = getNumLeafs(myTree) # 获取决策树叶结点数目,决定了树的宽度
depth = getTreeDepth(myTree) # 获取决策树层数
firstStr = next(iter(myTree)) # 下个字典
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff) # 中心位置
plotMidText(cntrPt, parentPt, nodeTxt) # 标注有向边属性值
plotNode(firstStr, cntrPt, parentPt, decisionNode) # 绘制结点
secondDict = myTree[firstStr] # 下一个字典,也就是继续绘制子结点
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD # y偏移
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
plotTree(secondDict[key], cntrPt, str(key)) # 不是叶结点,递归调用继续绘制
else: # 如果是叶结点,绘制叶结点,并标注有向边属性值
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
"""
函数说明:创建绘制面板
Parameters:
inTree - 决策树(字典)
"""
def createPlot(inTree):
fig = plt.figure(1, facecolor='white') # 创建fig
fig.clf() # 清空fig
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # 去掉x、y轴
plotTree.totalW = float(getNumLeafs(inTree)) # 获取决策树叶结点数目
plotTree.totalD = float(getTreeDepth(inTree)) # 获取决策树层数
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0; # x偏移
plotTree(inTree, (0.5, 1.0), '') # 绘制决策树
plt.savefig("./BT.png")
plt.show()
if __name__ == '__main__':
dataSet, labels = createDataSet()
featLabels = []
myTree = createTree(dataSet, labels, featLabels)
print("决策树结构:{}".format(myTree))
testVec = [0, 1, 1, 1] # 测试数据
result = classify(myTree, featLabels, testVec)
if result == 'yes':
print('可贷')
if result == 'no':
print('不可贷')
createPlot(mytree)
 、
、
7.决策树结构可视化
8.使用sklearn中决策树算法
点击查看代码
import numpy as np
import random
from sklearn import tree
from graphviz import Source
import pandas as pd
import re
def origalData():
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
if __name__ == '__main__':
dataset,labels = origalData()
datasetFrame = pd.DataFrame(dataset)
print("datasetFrame:{}".format(datasetFrame))
X_train = datasetFrame.iloc[:,:-1]
Y_train = datasetFrame.iloc[:,4:]
a = np.column_stack((Y_train,X_train))
clf = tree.DecisionTreeClassifier(criterion='gini',max_depth=4)
clf =clf.fit(X_train,Y_train)
graph = Source(tree.export_graphviz(clf,out_file=None))
graph.format='png'
graph.render('dtYesNo',view=True)
print('X_train:{}\nY_train:{}'.format(X_train,Y_train))
# print("dataset:{}\nlabels:{}".format(dataset,labels))
10.针对iris数据集,应用sklearn的决策树算法进行类别预测
点击查看代码
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label']=iris.target
df.columns = ['speal length','speal width','petal length','petal width','label']
data = np.array(df.iloc[:100,[0,1,-1]])
print('data:')
print(data)
if __name__ == '__main__':
iris = load_iris()
X,y = create_data()
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
#print(X_train,X_test,y_train,y_test)
clf = DecisionTreeClassifier(criterion='gini',max_depth=4)
print(clf.fit(X_train,y_train,))
print(clf.score(X_test,y_test))
graph = Source(tree.export_graphviz(clf, out_file=None))
graph.format = 'png'
graph.render('dt', view=True)

12.鸢尾花决策树的结构
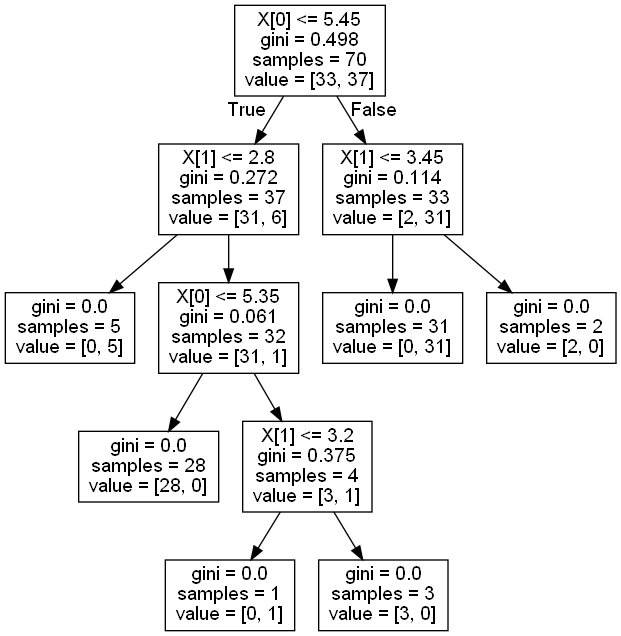
实验小结
- ID3算法基本原理
ID3作为一种经典的决策树算法,是基于信息熵来选择最佳的测试属性,其选择了当前样本集中具有最大信息增益值的属性作为测试属性。
样本集的划分则依据了测试属性的取值进行,测试属性有多少种取值就能划分出多少的子样本集;同时决策树上与该样本集相应的节点长出新的叶子节点。
ID3算法根据信息论理论,采用划分后样本集的不确定性作为衡量划分样本子集的好坏程度,用“信息增益值”度量不确定性——信息增益值越大,不确定性就更小,这就促使我们找到一个好的非叶子节点来进行划分。
1.我们假设一个这样的数据样本集S,其中数据样本集S包含了s个数据样本,假设类别属性具有m个不同的值(判断指标):Ci(i=1,2,3,…,m)
S是C中的样本数,对于一个样本集总的信息熵为:
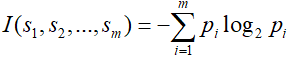
其中,Pi表示任意样本属于Ci的概率,也可以用si/s 进行估计。
我们假设一个属性A具有k个不同的值 {a1,a2,…,ak}, 利用属性A将数据样本S划分为k个子集{S1,S2,…, Sk},其中Sj包含了集合S中属性A取aj值的样本。若是选择了属性A为测试属性,则这些子集就是从集合S的节点生长出来的新的叶子节点。
设Sij是子集Sj中类别为Ci的样本数,则根据属性A划分样本的信息熵值为:
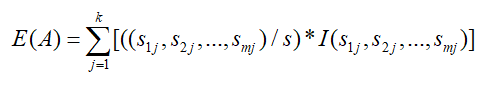
最后,我们利用属性A划分样本集S后得到的信息熵增益为:
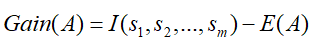
ID3算法是经典的决策树算法,但是随着时间的发展,出现的C4.5算法弥补了许多ID3算法在使用信息增益率来选择节点属性的不足之处。
- C4.5算法基本原理
C4.5是决策树算法的一种。决策树算法作为一种分类算法,目标就是将具有p维特征的n个样本分到c个类别中去.
C4.5算法是用于生成决策树的一种经典算法,是ID3算法的一种延伸和优化。C4.5算法对ID3算法主要做了一下几点改进:
(1)通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足;
(2)能够处理离散型和连续型的属性类型,即将连续型的属性进行离散化处理;
(3)构造决策树之后进行剪枝操作;
(4)能够处理具有缺失属性值的训练数据。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 本地部署DeepSeek后,没有好看的交互界面怎么行!
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 趁着过年的时候手搓了一个低代码框架
· 推荐一个DeepSeek 大模型的免费 API 项目!兼容OpenAI接口!
· 用 C# 插值字符串处理器写一个 sscanf