numpy-record

本篇只是学习NumPy时的一本记录本，仅用于本人记录不熟点和未知点，后续回顾使用。

编辑器：Jupyter Notebook

ipykernel:Python3

使用linspace/logspace生成

np.linspace(开头，结尾，数量)

linspace更适用于生成一个线性数据局(元素是等差关系)

而logspace(开头，结尾，数量，base=底数)

logspace更适用于生成一个指数函数数据(元素是等比关系)

#导入matlab的python库
import matplotlib.pyplot as plt
import numpy as np
#准备数据
N = 10
x = np.arange(N)#x轴数据
y1 = np.linspace(0,10,N)* 100#y轴数据
y2 = np.logspace(0,10,N,base=2)#y轴数据
#创建画布
plt.figure()
#将数据画入画布
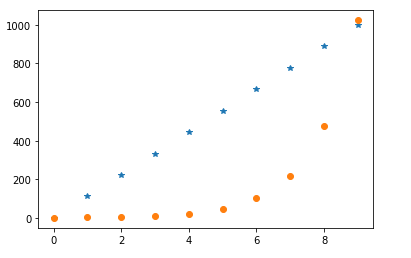
plt.plot(x, y1, '*')
plt.plot(x, y2, 'o')
#显示画布
plt.show()

矩阵元素判断

构建矩阵并进行元素判断

#创建矩阵
a  = ((2,3),(3,4))
b = np.array(a,dtype=np.float32)
#创建元素判断结果矩阵，注意，矩阵在条件筛选的时候，是对矩阵中的所有元素依次比较，并将结果以布尔矩阵进行返回
r = b>3
print(r)
'''
>>
result: array([[False, False],
        [False,  True]])'''

将返回的布尔矩阵进行判断

#承接上述代码,我们将返回的布尔矩阵进行判断
#此处使用的是逻辑运算,any()/all() 注意：不能使用if进行判断，因为它是矩阵！！！
#any()为只要有true，就返回true
print(r.any())
>>False
#all()需要所有元素都为true，才返回true
print(r.all())
>>True

创建全0或全1矩阵

#np.zeros(维数)
#np.ones(维数)
#np.zeros/ones_like(矩阵)
print(np.ones((2,3,5)))
print('\n\n')
print(np.zeros((2,3,5)))
print(np.ones_like(np.zeros((2,3,5))))

random生成

#生成范围为0~1的连续均匀分布的随机数
np.random.rand(2,3)
#生成指定上下界的连续分布
np.random.uniform(-1,1,(2,3))

#规范点是创建一个随机数生成器，后续创建随机数时使用rng为前缀
rng = np.random.default_rng(1)
rng.uniform(low=-1,high=1,size=(3,4))
#使用生成器创建正态分布和均匀分布
#正态分布，loc分布的均值，scale分布的标准差,size输出值维度
rng.normal(loc=0.0,scale=1.0,size=(2,3))
#均匀分布,low\high为下\上界
#离散型
rng.integers(low=0,high=10,size=(2,3))
#连续性
rng.uniform(low=-1,high=10,size=(2,3))

• numpy.random.shuffle(a):将数组a中的元素随机排列。
• numpy.random.permutation(a):将数组a中的元素随机排列，但不保持原有顺序。

将array保存为文件

# 直接将给定矩阵存为 a.npy
np.save('./data/a', np.array([[1, 2, 3], [4, 5, 6]]))

# 可以将多个矩阵存在一起，名为 `b.npz`
np.savez("./data/b", a=np.arange(12).reshape(3, 4), b=np.arange(12.).reshape(4, 3))

# 加载单个 array
np.load("data/a.npy")
# 加载多个，可以像字典那样取出对应的 array
arr = np.load("data/b.npz")
arr["a"]
arr['b']

元素统计和矩阵属性

矩阵属性

矩阵尺度

#查看矩阵维度
arr["b"].ndim
>>2
#查看矩阵每个维度的实际大小
arr['b'].shape 
>>(4,3)
#矩阵元素个数
arr['b'].size
>>12

元素统计

#axis指定按行1还是列0查找符合元素
#最大数
arr['b'].max(axis = 1)
#最小数
arr['b'].min(axis = 1)

#注意：在深度学习中的很多情况下，是需要数据保持原有维度方便后续计算
#使用参数：keepdims=True来保持，不适用这个参数时，一般返回一维数据
arr['b'].min(axis = 1,keepdims=True)#保持了行维度

#或者使用amax()/amin()，来根据输入矩阵，按指定的行或列进行返回结果，但仍为一维
np.amin(arr['b'],axis=0,keepdims=True)

#中位数
np.median(arr['b'])

#分位数
#分位数是将数据分成相等部分的值，通常用于描述数据的分布情况和比较不同数据集之间的差异。
# 分位数，按行取 3/4，同时保持维度
np.quantile(arr['b'], q=0.75, axis=1, keepdims=True)

分位数解释：

分位数(Quartile)是将一组数据分成四个部分的统计量，也称为四分位数。它表示了数据的中间50%的范围，即第25个百分位数和第75个百分位数之间的值。
例如，如果一个样本有100个数据点，那么可以将它们分成四组，每组包含25个数据点。
第一组包含最小值和第二小值，第二组包含第二小值和第三小值，第三组包含中位数和第四小值，第四组包含最大值和中位数。
这四个部分分别对应着第一四分位数、第二四分位数、中位数和第三四分位数。

元素计算

#需要注意的是，以下函数都可以指定按行或列进行计算
#平均值
np.average(arr['b'],axis=1)
#求和
np.sum(arr['b'])
#累计求和
np.cumsum(arr['b'],axis=1)
#标准差
np.std(arr['b'])
#方差
np.var(arr['b'],axis=1)

形状转换

转置

#二维常用
arr.T
#三维以上
np.transpose(arr)
#当transpose指定列数交换顺序时
#如：交换2、3列元素
np.transpose(arr.reshape(4,1,3,1),axes=(0,2,1,3))

改变形状*

b = np.copy(a)
#将数据转换为一维
b.ravel()

#扩充维度
#np.expand_dims(arr,axis=(扩充列索引))
np.expand_dims(a,axis=(1,3,4))
#降低维度，注意：只能去除维度为1的
#np.squeeze(arr,axis=(降低维度索引))

#arr.reshape()

#arr.resize((),refcheck=False/True),原地变换形状，且不能使用-1.
#使用参数refcheck=False/True，用于当矩阵改变形状时
#若多于原矩阵形状，是否使用户0填充；否则会截断

分解和组合**

切片和索引

切片和索引是通过对已有 array 进行操作而得到想要的「部分」元素的行为过程。其核心动作可以概括为：按维度根据 start:stop:step 操作 array。

不进行处理的维度统一使用:或...代替，如：arr[::,-1]==arr[...,-1]

#有几行就有几个:
#比如二维的矩阵，为arr[:,:] == arr[::] == arr[:]
#:表示取连续的数据
arr[:,1]
#[,]表示取离散型的数据
arr[:,[1,2]]

拼接

np.concatenate 和 np.stack，前者是拼接，后者是堆叠（会增加一个维度），都可以指定维度。

#拼接
np.concatenate((a,b),axis=1)
>>
array([[   0.        ,  111.11111111,  222.22222222,  333.33333333,
         444.44444444,    0.        ,  111.11111111,  222.22222222,
         333.33333333,  444.44444444],
       [ 555.55555556,  666.66666667,  777.77777778,  888.88888889,
        1000.        ,  555.55555556,  666.66666667,  777.77777778,
         888.88888889, 1000.        ]])
#堆叠
np.stack((a,b))
>>
array([[[   0.        ,  111.11111111,  222.22222222,  333.33333333,
          444.44444444],
        [ 555.55555556,  666.66666667,  777.77777778,  888.88888889,
         1000.        ]],

       [[   0.        ,  111.11111111,  222.22222222,  333.33333333,
          444.44444444],
        [ 555.55555556,  666.66666667,  777.77777778,  888.88888889,
         1000.        ]]])

重复

也就是指定某个维度重复(或者说某个维度增加)

np.repeate(arr,dim_num,axis=)

分拆

即将矩阵的某个(axis)维度拆成dim_num份

np.split(arr, dim_num, axis=)
# （axis=1）切分行
np.split(arr, 2, axis=1)

筛选和提取**

筛选

#利用条件筛选，返回布尔矩阵
arr > 50 #返回满足条件的布尔矩阵
#将不满足条件的元素进行修改
np.where(条件, arr , 修改值)

提取

#将矩阵的元素进行提取出来
#提取符合条件的值
np.extract(条件,arr)
#提取唯一值
np.unique(arr)

抽样

rng = np.random.default_rng(42)
# 第一个参数是要抽样的集合，如果是一个整数，则表示从 0 到该值
# 第二个参数是样本大小
# 第三个参数表示结果是否可以重复
# 第四个参数表示出现的概率，长度和第一个参数一样
rng,choice(1 ,2 , 3, 4)
# 由于（0 1 2 3）中 2 和 3 的概率比较高，自然就选择了 2 和 3
rng.choice(4, 2, replace=False, p=[0.1, 0.2, 0.3, 0.4])

#旧API
data_size= 
np.random.choice(data_size,50,replace=False)

最值的索引

#可选择是否按行或列排序，默认按行排序且从小到大
np.argmax/argmin(arr,axis=)
np.argsort()

算术

常见运算

#利用生成器生成测试矩阵
b_rng = np.random.default_rng(2)
b = b_rng.integers(2,20,(3,6))

#开方再平方再乘2
np.sqrt(a) ** 2 * 2
a[0,0] = 1

#对数化
np.log(a)

#超过num元素的都换成num
#np.minimum(arr,num)
np.minimum(b,7)
#小于num元素的都换成num
#np.maximum(arr,num)
np.maximum(b,7)

#四舍五入
np.round(a)

#向上取整ceil，向下取整floor
np.ceil(arr)
np.floor(arr)

#对元素进行取余
#np.mod(arr,num)，num可以以动态数

广播机制

其作用于，将不同形状的矩阵按不同的形式，适配对方。

需要注意的是：广播机制要求小矩阵至少有一部分时符合大矩阵的维数。

例如，假设我们有一个形状为(3, 4)的大矩阵A和一个形状为(3, 1)的小矩阵B:

A = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

B = np.array([[2], [3], [4]])

此时NumPy会对矩阵B进行扩展：

B=[[2,2,2,2],[3,3,3,3],[4,4,4,4]]
A+B
>>
array([[ 3,  4,  5,  6],
       [ 8,  9, 10, 11],
       [13, 14, 15, 16]])

点积和乘积**

需要注意的是，两者都需要其符合矩阵相乘的充要条件。

#dot，向量点积
#np.dot(arr1,arr2)
np.dot(a,a.T)
#matmul，矩阵乘积
#np.matmul(arr1,arr2)
np.matmul(a,a.T)

数学角度

在高维矩阵的理解是，假设有n维矩阵，那么其元素为n-1维矩阵。

而高维矩阵相乘的理解是，将其拆分到2维矩阵，因为矩阵乘法的本质是从2维矩阵来看的，那么我们需要高维矩阵拆分为2维的矩阵进行判断是否可相乘。

#例如:a的形状为(5,2,3,4)
#b的形状为(5,4,4,2)
#其结果的矩阵形状为(5,2,3,2)
#理解：因为高维矩阵相乘需要将其拆分为2维矩阵，而2维矩阵其实就是高维矩阵形状的最后两位数，是要看它们是否满足矩阵乘法的充要条件即可。

dot和matmul函数的区别

dot函数对于高维数组时，会将其展平为一维数组，并在内部使用一维数组的运算规则来计算。因此，在使用dot时需要注意数组形状的匹配，以避免出现不符合预期的结果。

matmul函数则能够处理高维数组，并且使用矩阵乘法的规则来计算。当两个参数都是二维矩阵时，matmul函数与dot函数的行为是一致的，但是当参数是高维数组时，matmul函数会将最后两维视为矩阵，对它们进行矩阵乘法计算，并沿着其他维度进行广播。

注意：

我们需要知道的是在numpy的高维矩阵相乘中，使用matmul函数，还需要其参数两者的最外层维数需要相同，因为其维度不能改变。

dot函数常用于高维矩阵的升维。

请结合以下两个例子理解区别：

#高维矩阵中，点积将前者的一维行向量与后者的一维列向量相乘
#如下例子中:前者的每个1x3行向量与后者的列向量(3x1)相乘，得到的后者形状变为(4,6)
#并将后者作为前者的列向量的元素(5,2,x(4,6))
in:np.dot( np.ones((5, 2, 3)), np.ones((4, 3, 6)) ).shape
out:(5, 2, 4, 6)

#在高维矩阵中，使用矩阵乘法，会分解到2维向量相乘。
in:np.matmul( np.ones((4, 2, 3)), np.ones((4, 3, 6)) ).shape
out:(4, 2, 6)

其他运算

A = np.array(((1,2),(1,1)))
#内积
np.inner(A,A)
A.dot(A.T)
#点积
np.vdot(A,A)
np.sum(A*A)
#行列式
np.linalg.det(A)
#逆矩阵(方阵)
np.linalg.inv(A)

我们需要知道的是逆矩阵需要参数方阵不为奇异矩阵。