day07--二维数组 & 递归
今天我们主要学习以下内容
1. 二维数组的概念,内存映象,二维数组中数据元素的访问
2. 二维数组的3中初始化方式
3. 方法的参数传递问题(基本数据类型和引用数据类型)
4 递归方法的定义,递归的算法核心思想
二维数组
引例:
我们已经学习了基本的一维数组,可以持有大量数据。
思考如下场景: 假设我现在要统计,学校中某个年级中,各班的数学成绩的平均分。 思考一下,用一维数组可以吗?会遇到什么问题? 分析一下出现问题的原因是什么呢? 不同的维度
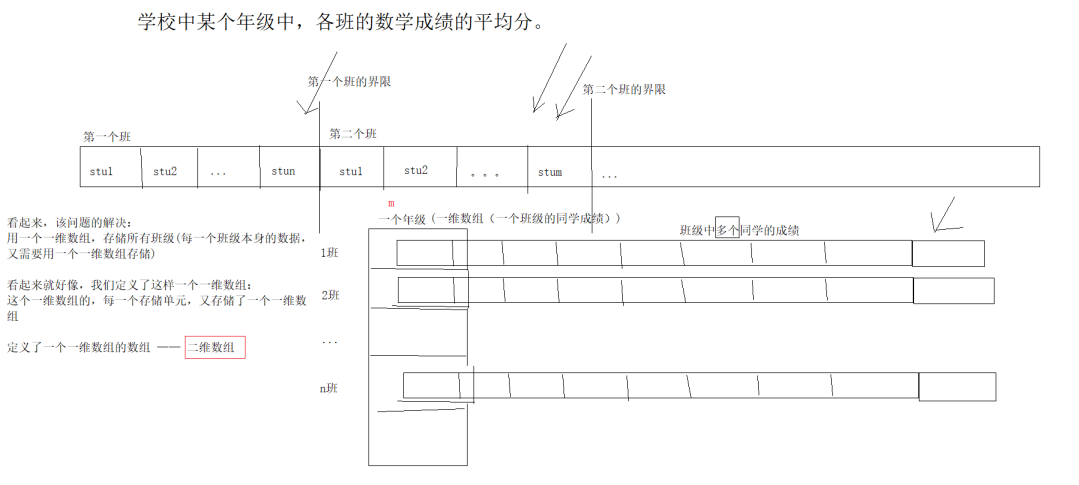
图:二维数组的引例
二维数组初始化三种格式

图:二维数组的初始化格式1
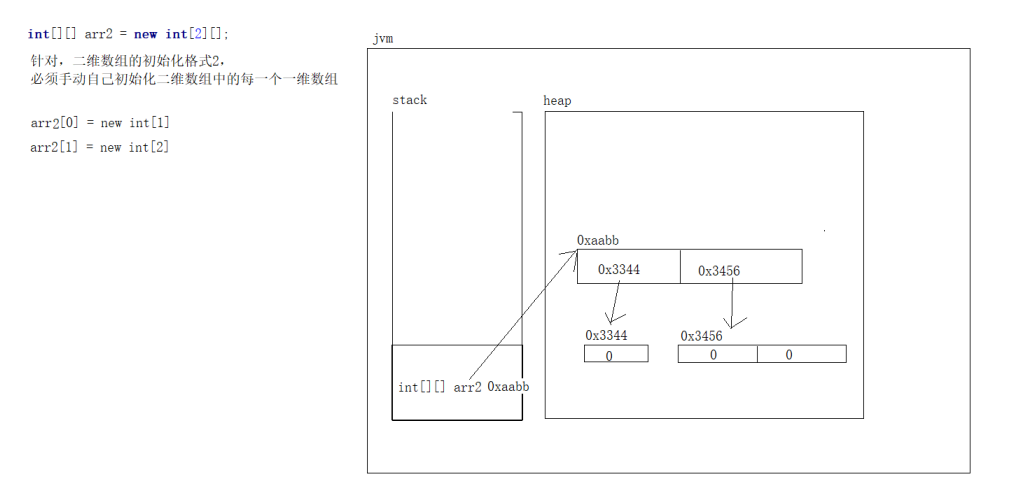
图:二维数组的初始化格式2
1 package com.cskaoyan.two; 2 3 /** 4 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 5 * @version 1.0 6 * 二维数组的实质:一维 (数组的) 数组 7 8 二维数组的初始化格式1: 9 数据类型[][] 变量名 = new 数据类型[m][n]; 10 m代表二维数组中一维数组的个数 11 n代表二维数组中包含的每个一维数组,所能包含的元素个数 12 特征:二维数组中每一个一维数组包含的元素个数相同 13 14 二维数组定义的格式2 15 数据类型[][] 变量名 = new 数据类型[m][]; 16 m表示这个二维数组有多少个一维数组 17 这一次没有直接给出一维数组的元素个数,可以动态的给出。 18 19 int[][] arr2 = new int[2][]; 20 arr[0] = new int[1]; 21 arr[1] = new int[2]; 22 特征: 初始化二维数组比较麻烦,二维数组中的一维数组,都需要我们自己初始化, 23 但可以让二维数组的每个一维数组包含不同的元素个数 24 25 26 二维数组定义的格式3 27 数据类型[][] 变量名 = new 数据类型[][]{{元素…},{元素…},{元素…}}; 28 29 简化版格式: 30 数据类型[][] 变量名 = {{元素…},{元素…},{元素…}}; 31 32 注意: 33 简化版只能在定义数组的引用变量时使用! 34 35 36 37 * 38 * 39 * 40 */ 41 public class Demo1 { 42 43 public static void main(String[] args) { 44 45 // 二维数组的初始化格式1: 46 // 数据类型[][] 变量名 = new 数据类型[m][n]; 47 firstInitialization(); 48 49 // 二维数组的初始化格式2: 50 // 数据类型[][] 变量名 = new 数据类型[m][]; 51 secondInitialiization(); 52 53 //二维数组定义的格式3 54 //数据类型[][] 变量名 = new 数据类型[][]{{元素…},{元素…},{元素…}}; 55 // 3个一维数组,每个一维数组的初值分别通过{}来指定 56 int[][] arr3 = new int[][] {{1}, {2, 3}, {4, 5, 6}}; 57 58 traverseTwoDimensionArray(arr3); 59 60 } 61 62 63 public static void traverseTwoDimensionArray(int[][] arr) { 64 //遍历二维数组,输出二维数组中的每一个值 65 // arr 指向的是代表二维数组的那个一维数组 arr.length 表示二维数组中的一维数组个数 66 // arr[i] 代表二维数组中的第i个一维数组 arr[i].length 表示的就是二维数组中第i个一维数组的元素个数 67 68 for (int i = 0; i < arr.length; i++) { 69 70 //完成,对二维数组中的一个一维数组的遍历 71 for (int j = 0; j < arr[i].length; j++) { 72 System.out.print(arr[i][j] + " "); 73 } 74 System.out.println(); 75 } 76 77 78 } 79 80 private static void secondInitialiization() { 81 // 数据类型[][] 变量名 = new 数据类型[m][]; 82 int[][] arr2 = new int[2][]; 83 //初始化二维数组中的第一个一维数组 84 arr2[0] = new int[1]; 85 //初始化二维数组中的第二个一维数组 86 arr2[1] = new int[2]; 87 } 88 89 private static void firstInitialization() { 90 91 92 // 一个包含2个一维数组,且每个一维数组中包含2个元素的 一个二维数组 93 int[][] arr = new int[2][2]; 94 95 // 访问一下二维数组 96 97 //1. 输出二维数组的引用变量的值 98 System.out.println(arr); //[[(表示一个二维数组) I@ 4554617c 99 // 2. 输出执行二维数组中,第一个一维数组的,引用的值 100 System.out.println(arr[0]); // [I@74a14482 101 102 //3. 访问二维数组中,一维数组的元素值 103 System.out.println(arr[0][0]); 104 105 arr[1][1] = 100; 106 System.out.println(arr[1][1]); 107 } 108 109 }
练习:
- 二维数组遍历
- 打印杨辉三角形(行数可以键盘录入)
1 package com.cskaoyan.two; 2 3 import java.util.Scanner; 4 5 /** 6 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 7 * @version 1.0 8 * 9 * 1.二维数组遍历 10 公司年销售额求和 11 某公司按照季度和月份统计的数据如下:单位(万元) 12 第一季度:22,66,44 13 第二季度:77,33,88 14 第三季度:25,45,65 15 第四季度:11,66,99 16 17 2. 打印杨辉三角形(行数可以键盘录入) 18 1 1 19 2 1 1 20 3 1 2 1 21 4 1 3 3 1 22 5 1 4 6 4 1 23 24 1. 对于杨辉三角而言,第一行和第二行数据是固定的 25 2. 每一行的元素个数和行数相同(从第1行开始) 26 3. 从第3行开始: 27 a. 每一行的第一个和最后一个元素值固定,都是1 28 b. 每一行出首尾位置之外,其他位置的元素值都有规律: 29 第i行第j列 = 第i - 1行第j列的值 + 第i-1行j - 1列 30 31 32 */ 33 public class Exercise { 34 35 public static void main(String[] args) { 36 37 // 第三种初始化二维数组格式的简化 38 int[][] sales = {{22,66,44}, {77,33,88}, {25,45,65}, {11,66,99}}; 39 //简化版只能在定义数组的引用变量时使用! 40 //sales = {{22,66,44}, {77,33,88}, {25,45,65}, {11,66,99}}; 41 //sales = new int[][]{{22,66,44}, {77,33,88}, {25,45,65}, {11,66,99}}; 42 43 //System.out.println(exercise01(sales)); 44 45 46 47 //练习2 48 Scanner scanner = new Scanner(System.in); 49 int n = scanner.nextInt(); 50 int[][] arr = exercise02(n); 51 traverseTwoDimensionArray(arr); 52 53 } 54 55 56 public static int exercise01(int[][] salse) { 57 int sum = 0; 58 59 for (int i = 0; i < salse.length; i++) { 60 61 for (int j = 0; j < salse[i].length; j++) { 62 sum += salse[i][j]; 63 } 64 } 65 66 return sum; 67 } 68 69 70 /** 71 * 72 * @param n 表示杨辉三角的行数 73 * @return 表示n行杨辉三角数据的二维数组 74 */ 75 public static int[][] exercise02 (int n) { 76 77 //针对第n值为1和n值为2,做特殊处理 78 if (n == 1) { 79 return new int[][]{{1}}; 80 } 81 82 if (n == 2) { 83 return new int[][]{{1}, {1, 1}}; 84 } 85 86 87 // 表示,最终返回的二维数组的结果 88 int[][] result; 89 // 用格式2初始化,结果二维数组 90 result = new int[n][]; 91 // 初始化杨辉三角的第一行和第二行数据 92 result[0] = new int[] {1}; 93 result[1] = new int[] {1, 1}; 94 95 // 从第3行开始,计算并初始化,每一行杨辉三角数据 96 for (int i = 2; i < n; i++) { 97 // 初始化杨辉三角第i + 1行 对应的第i个一维数组 98 result[i] = new int[i + 1]; 99 //对于杨辉三角的第i行数据, 初始化首尾元素的值 100 result[i][0] = 1; 101 result[i][i] = 1; 102 103 104 for (int j = 1; j < i; j++) { 105 //第i行第j列 = 第i - 1行第j列的值 + 第i-1行j - 1列 106 result[i][j] = result[i - 1][j] + result[i - 1][j - 1]; 107 } 108 } 109 return result; 110 } 111 112 public static void traverseTwoDimensionArray(int[][] arr) { 113 //遍历二维数组,输出二维数组中的每一个值 114 // arr 指向的是代表二维数组的那个一维数组 arr.length 表示二维数组中的一维数组个数 115 // arr[i] 代表二维数组中的第i个一维数组 arr[i].length 表示的就是二维数组中第i个一维数组的元素个数 116 117 for (int i = 0; i < arr.length; i++) { 118 119 //完成,对二维数组中的一个一维数组的遍历 120 for (int j = 0; j < arr[i].length; j++) { 121 System.out.print(arr[i][j] + " "); 122 } 123 System.out.println(); 124 } 125 126 127 } 128 129 }
看程序写结果,并总结基本类型和引用类型参数的传递问题(题目在备注部分)
1 package com.cskaoyan.method; 2 3 /** 4 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 5 * @version 1.0 6 * 7 * 总结一下: 8 * 9 * 在java语言中,不管参数的类型,是引用类型还是,基本数据类型,在实际参数和形式参数进行值传递的方式只有一种: 10 * 实际参数的值 复制一份 赋值给形式参数 11 * 12 * 所以,实参的值,其实就有两份,调用方法中一份,被调用方法中一份 13 * 14 * 1. 当方法的参数是基本数据类型的参数的时候, 15 * 参数有两份,同时参数对应的数据的值,也有两份 16 * 17 * 2. 当方法的参数是引用数据类型的时候 18 * 参数值有两份,但是两个数组类型引用变量,对应的值(数组),只有一个 19 * 20 * 21 */ 22 public class Demo1 { 23 24 public static void main(String[] args) { 25 26 //int a = 10; 27 //int b = 20; 28 //System.out.println("main a:" + a + ",b:" + b); 29 //change(a, b); 30 //System.out.println("main a:" + a + ",b:" + b); 31 32 33 34 int[] arr = {1, 2, 3, 4, 5}; 35 change(arr); 36 System.out.println(arr[1]); 37 } 38 39 public static void change(int a, int b) { 40 System.out.println("change a:" + a + ",b:" + b); 41 a = b; 42 b = a + b; // 2 * b 43 System.out.println("change a:" + a + ",b:" + b); 44 } 45 46 47 public static void change(int[] arr) { 48 for (int x = 0; x < arr.length; x++) { 49 if (arr[x] % 2 == 0) { 50 arr[x] *= 2; 51 } 52 } 53 } 54 }
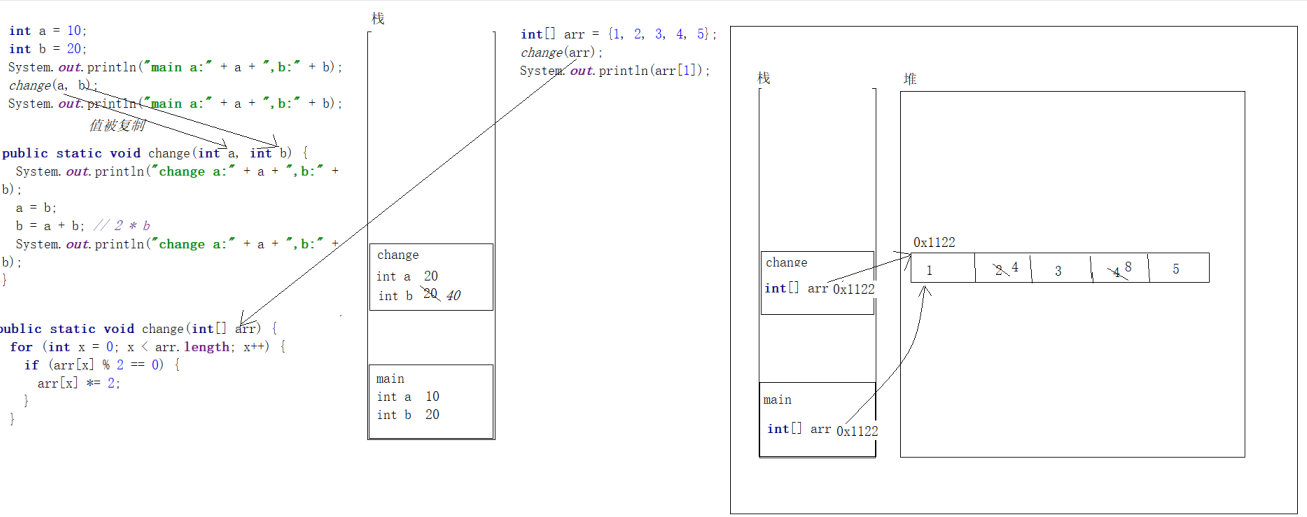
图:方法的参数传递
递归
递归定义:方法定义中调用方法本身的现象
实现递归需要注意的问题:
- 递归一定要有出口!!
- 次数不能太多,否则就出现 stack overflow

图:递归方法错误 & 栈内存管理
1 package com.cskaoyan.recursion; 2 3 /** 4 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 5 * @version 1.0 6 * 7 * 仅仅从语法角度: 8 * 递归方法定义:方法 定义中 调用 方法本身的方法 9 * 10 * 实现递归需要注意的问题: 11 1. 递归一定要有出口!!(递归一定要有终止条件,在一定条件下,终止自己调用自己) 12 2. 次数不能太多,否则就出现 stack overflow 13 * 14 */ 15 public class Demo1 { 16 17 public static void main(String[] args) { 18 19 //调用递归方法 20 //recursion1(); 21 22 //调用带递归出口的递归方法 23 recursion2(4); 24 25 //次数不能太多,否则就出现 stack overflow 26 recursion2(Integer.MAX_VALUE); 27 28 } 29 30 31 // 按照递归方法的定义来书写 java.lang.StackOverflowError 栈溢出错误 32 public static void recursion1() { 33 // 方法体中,自己调用自己 34 recursion1(); 35 } 36 37 38 /* 39 带递归出口的递归方法 40 */ 41 public static void recursion2(int n) { 42 43 //每一次调用自己之前,判断一下 n>0才自己调用自己,否则(n <= 0),终止自己调用自己 44 if (n <= 0) { 45 System.out.println("达到出口条件,不在自己调用自己 " + n); 46 return; 47 } 48 49 n--; 50 //否则,如果还没有达到递归的出口条件,继续自己调用自己 51 recursion2(n); 52 53 } 60 }
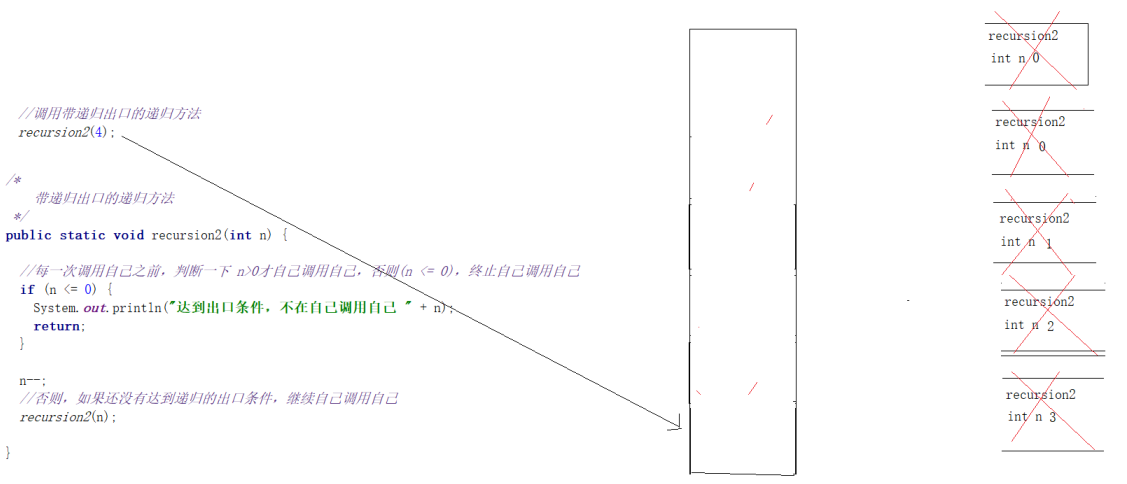
图:带出口条件的递归方法
例子:
1.汉诺塔问题:
有三根杆子A,B,C。A杆上有 N 个 (N>1) 穿孔圆盘,盘的尺寸由下到上依次变小。
要求按下列规则将所有圆盘移至 C 杆:
- 每次只能移动一个圆盘;
- 大盘不能叠在小盘上面。
提示:可将圆盘临时置于 B 杆,也可将从 A 杆移出的圆盘重新移回 A 杆,但都必须遵循上述两条规则。
问:最少要移动多少次?如何移?
2 3 /** 4 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 5 * @version 1.0 6 * 7 * 1.有三根杆子A,B,C。A杆上有 N(64) 个 (N>1) 穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆: 8 a. 每次只能移动一个圆盘; 9 b. 大盘不能叠在小盘上面。 10 提示:可将圆盘临时置于 B 杆,也可将从 A 杆移出的圆盘重新移回 A 杆,但都必须遵循上述两条规则。 11 问:最少要移动多少次?如何移? 12 13 14 解决思路以N个圆盘为例: 15 16 1. 当我们要解决N个圆盘的搬运问题,对于N个圆盘,我们可能无法一次性得到结果, 17 于是,我们把N个圆盘的搬运问题, -》 最大的云盘的搬运 & 最大圆盘上面的 n - 1 18 19 2. 对于规模为1那个待搬运的最大的圆盘,直接就知道如何搬运(一步搞定) 20 21 3. 在2的基础上,只要,解决 N - 1个圆盘搬运的问题 22 23 总结一下,汉诺塔问题,解决思路(递归算法的核心思想): 分而治之 24 把一个复杂的大规模的问题,分解成若干相似的小规模的子问题, 25 当问题规模,足够小的是时候,我们就可以直接得到小规模问题的解, 26 再把小规模问题的解,组合起来,——> 大规模问题提的解 27 28 29 1.用递归方法 -> 实现按照递归的方式,解决汉诺塔问题的代码 30 31 n 为3时的输出序列: 32 A——>C 33 A——>B 34 C——>B 35 A——>C 36 B——>A 37 B——>C 38 A——>C 39 40 2. n个圆盘,总共要搬运多少次,才能完成n个圆盘的搬运? 41 f(n) 表示n个圆盘搬运的次数 42 43 f(n) = f(n - 1) + 1 + f(n - 1) = 2 * f(n - 1) + 1 44 f(n) + 1 = 2(f(n - 1) + 1) 45 ... 46 f(1) + 1 = 2 47 48 {f(n) + 1} = 2^n 49 f(n) = 2^n - 1 50 51 52 */ 53 public class Demo2 { 54 55 public static void main(String[] args) { 56 57 //hanoi(3, 'A', 'C', 'B'); 58 59 System.out.println(count(3)); 60 61 } 62 63 // f(n) = f(n - 1) + 1 + f(n - 1) 64 public static int count(int n) { 65 66 // 出口条件 67 if (n == 1) { 68 return 1; 69 } 70 71 // 递归计算,n个圆盘搬运的的次数 72 73 return count(n - 1) + 1 + count(n - 1); 74 } 75 76 77 /** 78 * 79 * @param n 表示当前待搬运的圆盘的数量(代表当前问题的规模) 80 * @param start 当前待搬运的圆盘所在的杆的名字 81 * @param end 待搬运的n个盘盘,搬运到的目标杆的名字 82 * @param middle 此次把n个圆盘从start杆 -》 end杆时,所使用的辅助杆的名字 83 */ 84 public static void hanoi(int n, char start, char end, char middle) { 85 86 //递归方法的出口条件 87 if (n == 1) { 88 System.out.println(start + "——>" + end); 89 return; 90 } 91 92 //分解规模为n汉汉塔问题 93 94 // 将待搬运那上面的n-1个圆盘,搬运到辅助杆上 95 hanoi(n - 1, start, middle, end); 96 97 // 将起始杆上剩下的那个,待搬运的最大的圆盘,一次搬运到目标杆,它的最终位置 98 System.out.println(start + "——>" + end); 99 100 //接下来,对于剩余的在middle上的那n-1个圆盘,从middle杆开始,以start为辅助,移动到end杆上 101 hanoi(n - 1, middle, end, start); 102 } 103 104 }
2. 周末晚上你和女朋友去看电影,月黑风高,女朋友悄悄地问你:我们在第几排?电影院太黑,没办法数?怎么办?
1 package com.cskaoyan.recursion; 2 3 /** 4 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 5 * @version 1.0 6 * 7 * 2. 周末晚上你和女朋友去看电影,月黑风高,女朋友悄悄地问你:我们在第几排?电影院太黑,没办法数?怎么办? 8 * a. 无法直接看到,自己在第几排,但是我可以,问前排的同学,他在第几排 9 * b. 当依次向前询问,当问到第一排同学的时候,他可以用触觉来判断,比如,摸了一下发现前面没有椅子 10 * 11 * f(n) = f(n - 1) + 1 12 13 */ 14 public class Demo3 { 15 16 17 public static void main(String[] args) { 18 19 int row = f(10); 20 System.out.println(row); 21 } 22 23 24 /* 25 模拟,依次向前询问,自己在第几排,最终得到自己所在的排数 26 f(n) = f(n - 1) + 1 27 */ 28 public static int f(int n) { 29 30 if(n == 1) { 31 return 1; 32 } 33 34 //如果当前不是第一排的同学,就继续问他前排的同学 35 return f(n - 1) + 1; 36 } 37 38 }
3. 求n的阶乘
1 package com.cskaoyan.recursion; 2 3 /** 4 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 5 * @version 1.0 6 * 3. 求n的阶乘 7 f(n) = n * ((n - 1) * (n - 2) ... * 2 * 1) 8 f(n) = n * f(n - 1) 9 */ 10 public class Demo4 { 11 12 13 public static void main(String[] args) { 14 System.out.println(multiple(5)); 15 } 16 17 /** 18 * 19 * @param n 所求的问题规模 n的阶乘 20 * @return 21 * 22 * f(n) = n * f(n - 1) 23 * f(1) = 1 24 */ 25 public static int multiple(int n) { 26 27 if(n == 1) { 28 return 1; 29 } 30 31 return n * multiple(n - 1); 32 33 } 34 35 }
4. 求n的阶乘 4.有一对兔子,从出生后第三个月开始每月生一对兔子,小兔子从第三个月开始每月也生一对兔子,假如是不死神兔,那么第20个月一共生多少对兔子?
1 package com.cskaoyan.recursion; 2 3 /** 4 * @author zhangshuai@Cskaoyan.onaliyun.com on 2020/4/13. 5 * @version 1.0 6 * 7 * 4.有一对兔子,从出生后第三个月开始每月生一对兔子,小兔子从第三个月开始每月也生一对兔子, 8 * 假如是不死神兔,那么第20个月一共生多少对兔子? 9 * 10 * 月份 1 2 3 4 ... 11 兔子的数量 1 1 2 3 ... 12 13 14 i i + 1 i + 2 15 N(i) + N(i) = N(i) * 2 16 N(i - 1) + N(i - 1) * 2 = N(i - 1) * 2 + N(i - 1) 17 N(i - 2) + N(i - 2) * 2 = N(i - 2) * 2 + N(i - 2) 18 19 N(i) + N(i + 1) = N(i + 2) 20 21 count(n) = count(n - 1) + count(n - 2) 22 23 count(1) = 1 24 count(2) = 1 25 */ 26 public class Demo5 { 27 28 public static void main(String[] args) { 29 System.out.println(count(20)); 30 } 31 32 /* 33 计算不死神兔的数量 34 count(n) = count(n - 1) + count(n - 2) 35 */ 36 public static int count(int n) { 37 38 if(n == 1) { 39 return 1; 40 } 41 42 if (n == 2) { 43 return 1; 44 } 45 46 return count(n - 1) + count(n - 2); 47 48 } 49 50 51 52 53 54 /* 55 分析: 56 57 首先,我们设有n条直线时的答案为f(n) 58 1.那么当有n - 1条直线时,平面最多被分成了f(n - 1)个区域。 59 2.则第n条直线,如果要切成的区域数最多,那么第n条直线就必须与每条直线相交,且不能有同一交点。这样就会得到n - 1个交点。 60 3.而这些交点将这条直线(第n条直线)分为2条射线和n - 2条线段。而每条射线和线断将以有的区域一分为二。 61 这样就多出了2 + (n - 2),也就是n个区域。 62 63 f(1) = 2; 一条直线将一个平面分成2份 64 f(n) = f(n-1) + n; 65 66 */ 67 public static int f(int n) { 68 if (n == 1) { 69 return 2; 70 } 71 return f(n - 1) + n; 72 } 73 74 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号