Additive Quantization for Extreme Vector Compression 论文笔记
- 摘要
我们引入了一种新的高维矢量压缩方案,该方案使用来自M个不同码本的M个码字的和来近似矢量。 我们表明,所提出的方案允许压缩和未压缩矢量之间的有效距离和标量积计算。 我们进一步建议矢量编码和码本学习算法,其可以最小化所提出的方案内的编码误差。 在实验中,我们证明了所提出的压缩可以代替乘积量化或与乘积量化一起使用。 与乘积量化及其优化版本相比,所提出的压缩方法导致较低的编码近似误差,在视觉描述符的数据集中的近似最近邻搜索的较高准确度,以及较低的图像分类误差,无论何时在压缩上学习或应用分类器向量。
- 简介
在本文中,我们提出了一种称为加性量化(AQ)的新编码方法,它可以推广PQ并进一步提高PQ精度,同时在很大程度上保持其计算效率。与PQ类似,AQ将每个向量表示为几个组件的总和,每个组件来自单独的码本。与PQ不同,AQ不会将数据空间分解为正交子空间,因此不会进行任何子空间独立性假设。因此,每个AQ数据集内的码字具有与输入矢量相同的长度,并且通常彼此不正交。因此,与PQ不同,AQ中的码本是在联合优化过程中学习的。正如我们在强压缩视觉描述符的实验中证明的那样,去除独立性假设允许AQ获得比PQ更好的编码精度(图1),这转化为更高的最近邻搜索精度以及图像分类,每当分类器被学习或应用于压缩矢量时。
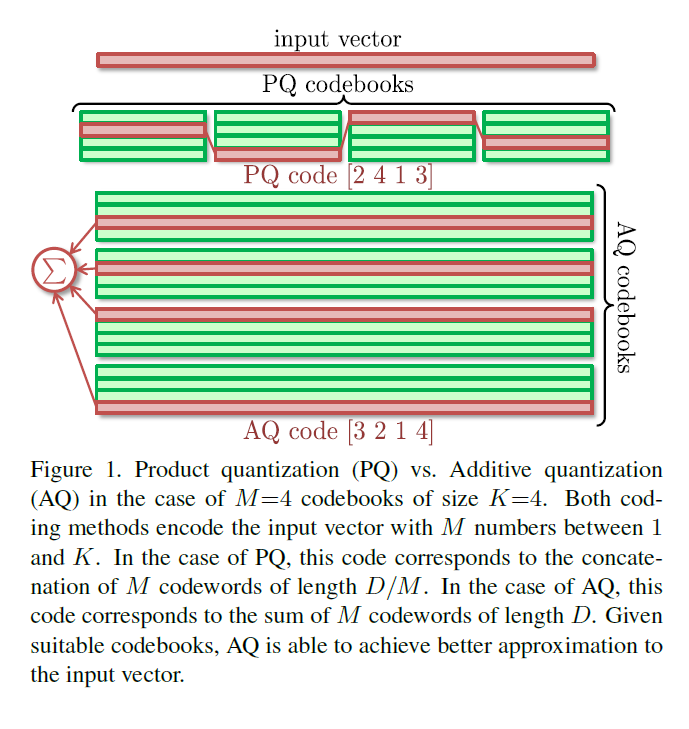
至关重要的是,我们表明,与PQ类似,AQ允许使用未压缩向量的基于查找表的非对称距离和标量积计算。 对于PQ通常使用的小型码本,AQ的标量积计算效率与PQ几乎相同。 与PQ相比,具有AQ的距离计算(ADC)需要少量额外时间或少量额外存储器,这在许多应用中通过提高的准确度是合理的。 编码,码本学习,距离计算和对PQ的改进,对于短码(例如,四个或八个字节)即极端压缩率都特别有利。 对于更长的代码,可以无缝地组合这两种技术(AQ和PQ)。
除了PQ之外,AQ还与计算机视觉和一般模式分析中流行的其他几个框架相连。 特别地,AQ可以被视为具有单位分量权重的稀疏编码的非常特殊的情况。 下面,我们还展示了AQ和马尔可夫随机场优化之间的有趣联系。 最后,AQ可以看作是标准矢量量化的推广,我们为AQ提出的码本学习算法是k-means算法的推广。
在本文的其余部分,我们讨论了AQ使用的表示,基于查找表的标量乘积和距离计算,AQ表示的编码算法以及码本学习。 然后,我们在最近邻搜索和图像分类的背景下,在AQ,PQ(包括优化版本[15])之间进行广泛的实验比较。
- 加性量化
我们现在引入符号并详细讨论加法量化(AQ)。 下面,我们假设我们处理D维向量。 AQ基于一组M个码本,每个码本包含K个向量(码字)。 我们将第m个码本表示为Cm,将第m个码本中的第k个码字表示为cm(k)。 此设置类似于PQ。 然而,在PQ中,码字具有长度D = M,AQ中的码字长度是D,即它们具有与正被编码的矢量相同的维度。
AQ模型将矢量x∈RD编码为M个码字的总和(每个码本一个码字)。 更详细地,矢量用码元的M元组编码[i1;I2; ::: ;; iM],其中每个ID在1和K之间。 编码过程(如下所述)寻找最小化x与相应码字之和之间距离的码:

如果,例如K = 256(如在我们的大多数实验中那样),则将矢量编码为M个字节,每个字节编码单个码字ID。 AQ编码矢量的存储器占用空间将与PQ编码矢量(对于相同的M和K)相同,而AQ可以更准确地表示矢量。 AQ中的码本占用的内存比PQ多M倍,但是对于足够大的数据集,这种内存增加通常可以忽略不计。
- 实验
在本节中,我们提供了对所提出的方法(加法量化)以及乘积量化[10]的一些比较评估的结果,以及称为笛卡尔K均值的优化乘积量化(OPQ)的一个版本 [15](使用作者的实现)。 这些基于PQ的方法代表了矢量压缩的最新技术,并且在最近的一些比较中已被证明比二进制编码方法表现更好[15,3]。
我们将注意力集中在小码本大小(K = 256)和极端压缩级别(M = 8和M = 16)上。 对于长度为M = 8和更长的码,我们还考虑使用OPQ优化来旋转数据然后将AQ编码(4个字节)应用于旋转矢量的不同部分的混合算法(加法乘积量化)(例如, 在8字节码长的情况下为一半,或在16字节码长的情况下为四分之一)。 在整个实验中,所有码本和旋转矩阵都在保持集上学习。 在所有实验中,我们在码本学习期间将波束搜索中的参数N设置为16,并且在数据编码期间将参数N设置为64。
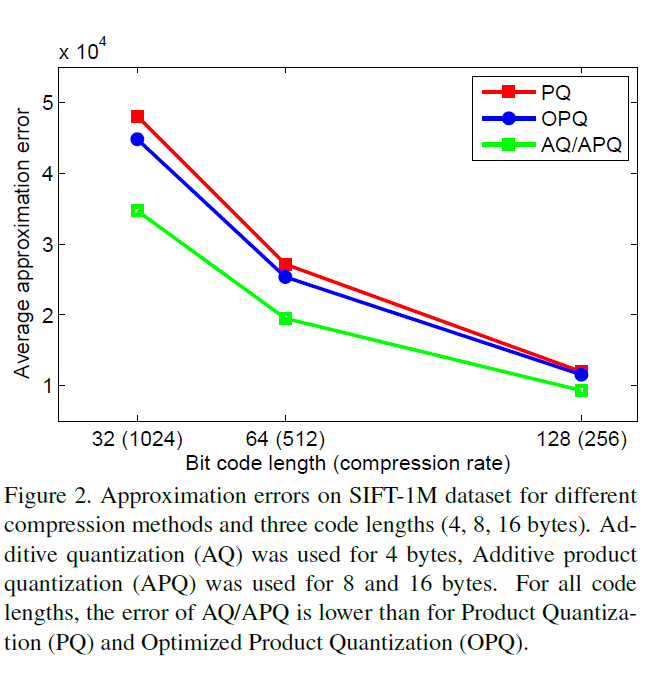
我们首先比较方法之间的近似误差。 在图2中,我们绘制了平均近似误差作为包含一百万个128维SIFT向量(加上保持集)的众所周知的SIFT1M数据集[10]的代码长度的函数。 对于所有代码长度(M = 4; 8; 16),AQ / APQ近似误差远低于当前最先进的方法PQ和OPQ。 鉴于这些令人鼓舞的结果,我们考虑两种应用,其中更准确的编码可以产生更好的性能,即(i)近似最近邻搜索和(ii)具有有限存储器的图像分类。
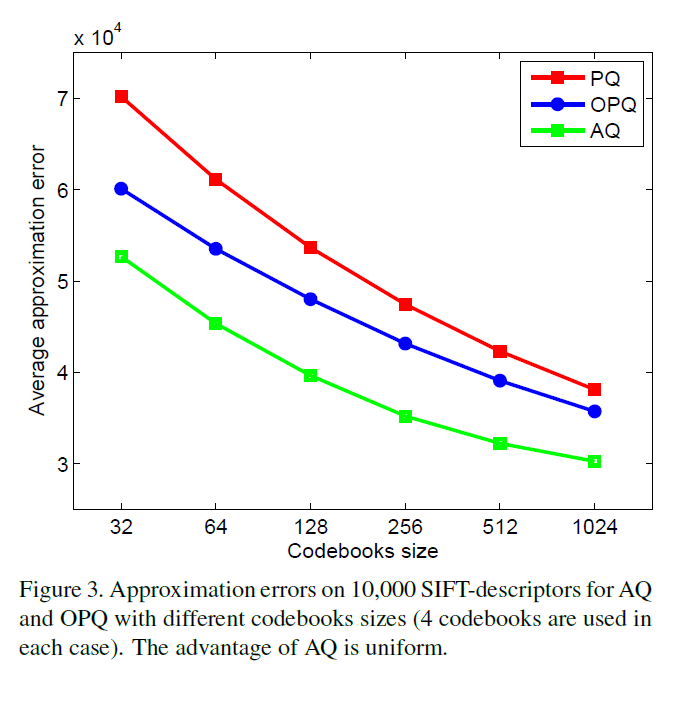
我们还针对变化的码本大小K执行AQ和OPQ近似质量的比较。图3示出了AQ为整个K范围提供了明显更好的压缩。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号