Optimized Product Quantization 论文笔记
- 摘要
乘积量化(PQ)是一种有效的矢量量化方法。乘积量化器可以以非常低的存储器/时间成本生成指数大的码本。 PQ的本质是将高维向量空间分解为子空间的笛卡尔乘积,然后分别量化这些子空间。最佳空间分解对于PQ性能很重要,但仍然是一个未解决的问题。在本文中,我们通过最小化空间分解和量化码本的量化失真来优化PQ。我们为这一具有挑战性的优化问题提出了两种新颖的方案:第一个解决方案迭代地解决了两个更简单的子问题;第二种解决方案基于高斯假设,并提供最优性的理论分析。我们在三个应用中评估我们的优化乘积量化器:(i)用于详尽排序的紧凑编码[1],(ii)为非穷举搜索构建反向多索引[2],以及(iii)用于图像检索的压缩图像表示[ 3]。在所有应用中,我们的优化乘积量化器优于现有解决方案。
- 简介
在本文中,我们将PQ表示为一个优化问题,通过寻找最佳码字和空间分解来最小化量化失真。由于大量未知参数,这种优化问题具有挑战性。在这项工作中,我们提出两种解决方:在第一个解决方案中,我们迭代地解决了两个更简单的子问题:用固定的码字求解空间分解,反之亦然。该解决方案是非参数的,因为它不假设关于数据分布的任何先验信息。我们的第二个解决方案是参数解决方案,因为它假设数据遵循高斯分布。在这个假设下,我们推导出量化失真下界的分析公式。然后我们理论上证明当(i)子空间相互独立时,这个下界被最小化,同时(ii)矢量在所有子空间中具有平衡的方差。基于这些理论,我们提出了一种简单的特征值分配方法来有效地优化空间分解。
我们通过实验证明了我们三种应用中的方法的优越性
- 当用于穷举搜索的紧凑编码时,我们的方法优于PQ和其他VQ方法的几种变体。 我们的方法也比各种最先进的二值化方法好得多。
- 当用于构建倒排索引时,我们的方法通过优化其码本来改进“反向的多索引”[2]。当我们在反向多索引和紧凑编码的组合中采用优化的PQ时,性能可以进一步提高。是10亿SIFT数据集的最好的效果。
- 我们进一步应用我们优化的PQ压缩图像表示(VLAD [3]和Fisher矢量[11])进行图像检索。 我们的方法提供了比原始PQ编码方法更好的检索精度。
- 优化的乘积量化
我们使用量化失真作为目标函数来评估乘积量化器的最优性。 乘积量化器涉及将D维向量空间分解为M个子空间并计算每个子空间的子码本。我们同时考虑子码本和空间分解。
我们使用正交矩阵R来表示空间分解。 注意,尺寸的任何重新排序(置换)可以由正交矩阵表示。 所以R决定将空间分解成M个等维子空间的所有自由度。
考虑到子码本和空间分解,我们优化了以下目标:

在这个问题中,自由参数由子码本(C1; ...; CM)和空间分解R组成。R的附加自由参数允许向量空间旋转,从而放松对码字的约束。 因此,与预先固定的R相比,优化的乘积量化器可以减少量化失真。
将x分配给最近的码字c相当于将Rx分配给最近的Rc。 为了应用优化的量化器进行编码,我们只需要通过Rx预处理数据,其余步骤与PQ中的步骤相同。
- 一个非参数的解决方案

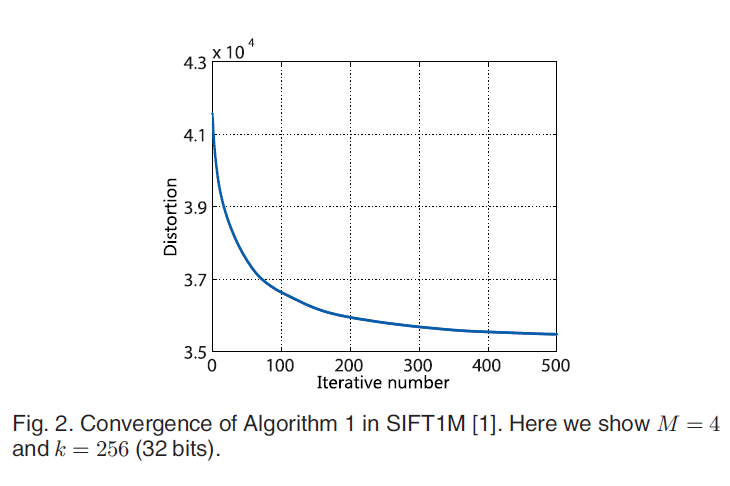
图2显示了我们算法的收敛性。 在实践中,我们发现100次迭代足以用于ANN搜索。 像许多其他交替优化算法一样,我们的算法是局部最优的,最终的解决方案取决于初始化。 在下一节中,我们提出了一个参数解决方案,当没有给出其他先验知识时,该解决方案可用于初始化上述迭代算法。
- 一个参数的解决方案
我们进一步提出另一种解决方案,假设数据遵循参数高斯分布。 该参数解决方案具有实际和理论上的优点。 首先,它是一种更简单的方法,如果数据遵循高斯分布,则是最优的。 其次,它提供了一种初始化非参数方法的方法。 第三,它为一些其他人工神经网络方法中两个常用标准提供了新的理论解释。



