Weighted-Entropy-based Quantization for Deep Neural Networks 论文笔记
---恢复内容开始---
- 摘要
量化被认为是优化神经网络模型的推理成本的最有效方法之一,用于部署到具有严格资源限制的移动和嵌入式系统。在这种方法中,在严格的精度损失约束(例如,1%)下提供低成本量化是至关重要的。在本文中,我们提出了一种基于加权熵概念量化权重和激活的新方法。与最近关于二进制加权神经网络的工作不同,我们的方法是多比特量化,其中权重和激活可以根据目标精度通过任意数量的比特量化。这有助于更灵活地利用由不同量化级别提供的准确性 - 性能权衡。此外,我们的方案提供了基于传统训练算法的自动量化流程,这大大减少了量化网络的设计时间。根据我们基于用于图像分类的实际神经网络模型(AlexNet,GoogLeNet和ResNet-50/101),物体检测(使用ResNet-50的R-FCN)和语言建模(LSTM网络)的广泛评估,我们的方法实现了模型大小和计算量显着减少,精度损失最小。此外,与现有的量化方案相比,我们提供了更高的精度和类似的资源约束,并且需要更低的设计工作量。
- 动机
最近的研究表明,卷积或完全连接层中的大多数权重集中在零附近,导致钟形分布。 激活值的分布是相似的,除了由于ReLU层激活值总是非负的。 现有量化方案基于这些特性以明智地分配量化级别。 例如,基于对数的量化(或LogQuant)通过将更多量化级别分配给接近零的值来利用接近零的权重的更密集分布。
除了权重/激活值的分布之外,我们还进行了一项关键观察,即在量化期间还应考虑每个权重/激活值对最终结果的影响。 由于量化方法的目的是使用最少的量化级别来最小化精度劣化,因此考虑到量化每个值的实际影响允许我们开发更有效地使用每个量化级别的新方案。 更具体地说,我们的见解可归纳如下:
- 近零值主导了重量和激活分布中的总频率值; 然而,它们对输出的影响很小(例如,非常小的权重误差可能不会对卷积的结果产生太大影响)。 因此,希望将较少的量化级别(简言之,本文中的级别)分配给接近零的值,而不是典型的基于线性或对数的量化。
- 大的重量和激活对产量的质量有重大影响,但它们并不常见。 因此,还希望为这些值分配少量的levels,以便最大化每个量化level的效用。
- 不属于上述两个类别的值具有相对大的数量,对输出质量具有显着影响。 因此,为这些值分配比传统量化更多的级别是有意义的方法。
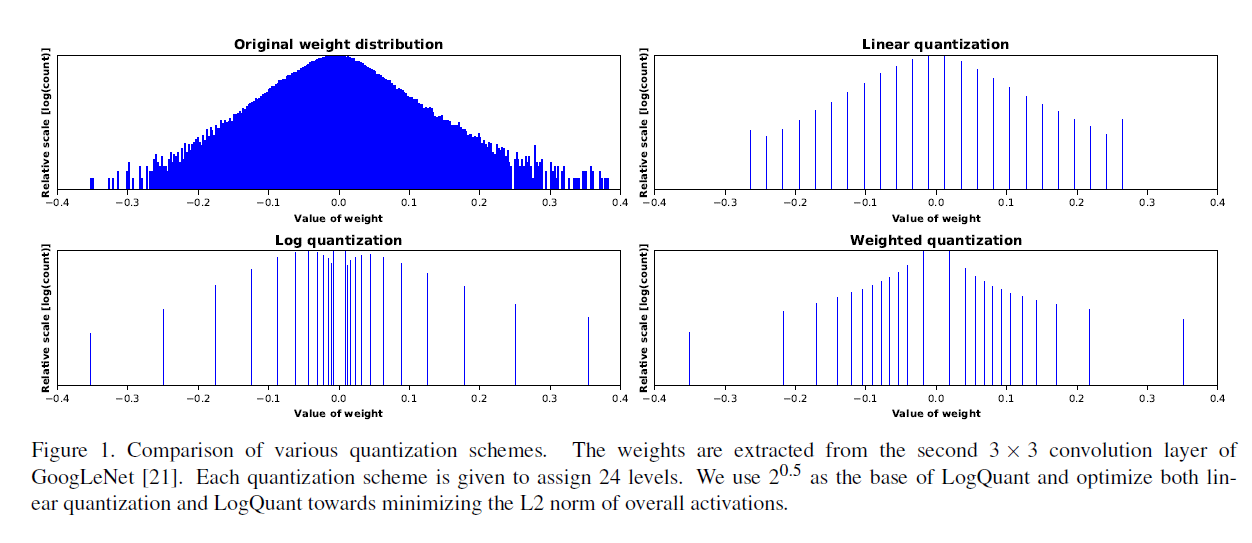
图1说明了现有方法和建议方法如何为给定的权重分布分配水平。 虽然线性量化根本不考虑权重分布,而LogQuant将过多的level分配给接近零的值,但我们的方法显示分布更集中于既不太小也不太大的值。 通过定量评估,我们稍后将展示这种量化方式比传统方案实现更高的效率。
- 基于加权熵的量化
- 权重量化
我们的权重量化方法的高级思想是将权重分组为N个群集,以便为重要的权重范围提供更多群集,为每个群集分配代表值,并将每个群集中的所有权重量化为代表值集群。 为此,我们必须能够评估群集质量并找到一组优化此类质量度量的群集。
基于每个权重的这个重要性值,我们导出用于基于加权熵来评估聚类结果(即,量化结果)的质量的度量。 加权熵源于物理学中的熵概念,旨在将数据的重要性考虑在内。 对于一组簇C0,...,CN-1,加权熵S被定义为

在该等式中,Pn表示在簇Cn的值范围内有多少权重,而In是簇Cn中所有权重的平均重要性。 粗略地说,用于大权重的簇通常具有高In但低Pn(即,高重要性但低频率),而用于小权重的簇将具有高Pn但低In(即,高频但低重要性)。 根据我们的实验,找到一个最大化S的聚类结果会产生量级被稀疏地分配给太小或太大的值的量化效果,正如我们在图1中所示。
算法1中显示了我们对此问题的解决方案。请注意,该算法仅显示非负权重的加权量化。 这是因为,由于加权熵理论的限制,我们无法获得具有负代表值和非负代表值的聚类结果。 因此,我们将权重分为两个负组和非负组,并将我们的算法应用于每个组,每组N / 2级。
在算法开始时,我们计算每个权重的重要性(第2和第3行)。 这是通过重要性映射函数fi完成的,该函数根据权重wk计算重要性ik。 在这项工作中,我们凭经验选择平方函数fi(w)= w2来计算每个权重的重要性。 在获得所有权重的重要性值之后,它们按其幅度的递增顺序排序(第4行)。

---恢复内容结束---
- 摘要
量化被认为是优化神经网络模型的推理成本的最有效方法之一,用于部署到具有严格资源限制的移动和嵌入式系统。在这种方法中,在严格的精度损失约束(例如,1%)下提供低成本量化是至关重要的。在本文中,我们提出了一种基于加权熵概念量化权重和激活的新方法。与最近关于二进制加权神经网络的工作不同,我们的方法是多比特量化,其中权重和激活可以根据目标精度通过任意数量的比特量化。这有助于更灵活地利用由不同量化级别提供的准确性 - 性能权衡。此外,我们的方案提供了基于传统训练算法的自动量化流程,这大大减少了量化网络的设计时间。根据我们基于用于图像分类的实际神经网络模型(AlexNet,GoogLeNet和ResNet-50/101),物体检测(使用ResNet-50的R-FCN)和语言建模(LSTM网络)的广泛评估,我们的方法实现了模型大小和计算量显着减少,精度损失最小。此外,与现有的量化方案相比,我们提供了更高的精度和类似的资源约束,并且需要更低的设计工作量。
- 动机
最近的研究表明,卷积或完全连接层中的大多数权重集中在零附近,导致钟形分布。 激活值的分布是相似的,除了由于ReLU层激活值总是非负的。 现有量化方案基于这些特性以明智地分配量化级别。 例如,基于对数的量化(或LogQuant)通过将更多量化级别分配给接近零的值来利用接近零的权重的更密集分布。
除了权重/激活值的分布之外,我们还进行了一项关键观察,即在量化期间还应考虑每个权重/激活值对最终结果的影响。 由于量化方法的目的是使用最少的量化级别来最小化精度劣化,因此考虑到量化每个值的实际影响允许我们开发更有效地使用每个量化级别的新方案。 更具体地说,我们的见解可归纳如下:
- 近零值主导了重量和激活分布中的总频率值; 然而,它们对输出的影响很小(例如,非常小的权重误差可能不会对卷积的结果产生太大影响)。 因此,希望将较少的量化级别(简言之,本文中的级别)分配给接近零的值,而不是典型的基于线性或对数的量化。
- 大的重量和激活对产量的质量有重大影响,但它们并不常见。 因此,还希望为这些值分配少量的levels,以便最大化每个量化level的效用。
- 不属于上述两个类别的值具有相对大的数量,对输出质量具有显着影响。 因此,为这些值分配比传统量化更多的级别是有意义的方法。
图1说明了现有方法和建议方法如何为给定的权重分布分配水平。 虽然线性量化根本不考虑权重分布,而LogQuant将过多的level分配给接近零的值,但我们的方法显示分布更集中于既不太小也不太大的值。 通过定量评估,我们稍后将展示这种量化方式比传统方案实现更高的效率。

- 基于加权熵的量化
- 权重量化
我们的权重量化方法的高级思想是将权重分组为N个群集,以便为重要的权重范围提供更多群集,为每个群集分配代表值,并将每个群集中的所有权重量化为代表值集群。 为此,我们必须能够评估群集质量并找到一组优化此类质量度量的群集。
基于每个权重的这个重要性值,我们导出用于基于加权熵来评估聚类结果(即,量化结果)的质量的度量。 加权熵源于物理学中的熵概念,旨在将数据的重要性考虑在内。 对于一组簇C0,...,CN-1,加权熵S被定义为

在该等式中,Pn表示在簇Cn的值范围内有多少权重,而In是簇Cn中所有权重的平均重要性。 粗略地说,用于大权重的簇通常具有高In但低Pn(即,高重要性但低频率),而用于小权重的簇将具有高Pn但低In(即,高频但低重要性)。 根据我们的实验,找到一个最大化S的聚类结果会产生量级被稀疏地分配给太小或太大的值的量化效果,正如我们在图1中所示。
算法1中显示了我们对此问题的解决方案。请注意,该算法仅显示非负权重的加权量化。 这是因为,由于加权熵理论的限制,我们无法获得具有负代表值和非负代表值的聚类结果。 因此,我们将权重分为两个负组和非负组,并将我们的算法应用于每个组,每组N / 2级。
在算法开始时,我们计算每个权重的重要性(第2和第3行)。 这是通过重要性映射函数fi完成的,该函数根据权重wk计算重要性ik。 在这项工作中,我们凭经验选择平方函数fi(w)= w2来计算每个权重的重要性。 在获得所有权重的重要性值之后,它们按其幅度的递增顺序排序(第4行)。



