打印二叉树边界

来到这边三年了，想换个工作，首先必须得过算法关，所以又开始了刷题之路。最近在看左程云的著作，里面的打印二叉树边界，其中的第二个标准的边界，从题目上就怎么也看不懂是什么规则，到网上去找清晰的分析，大部分也是

书上的简要描述和算法的实现，都没有过多的阐释那个规则是什么意思。甚至也有很多和我一样的，对第二题也是不甚了解的人在满脸疑惑地求解呢。求人不如求己，我是根据书上的题解，反推题目的具体含义，基本上弄懂了。

请先看题目，如下：

【题目】：

　　给定一颗二叉树的头节点 head，按照如下两种标准分别实现二叉树边界节点的逆时针打印。

　　标准一：

　　1、头节点为边界节点；

　　2、叶节点为边界节点；

　　3、如果节点在其所在的层中是最左或者最右的，那么也是边界节点。

　　标准二：

　　1、头节点为边界节点；

　　2、叶节点为边界节点；

　　3、树左边界延伸下去的路径为边界节点；

　　4、树右边界延伸下去的路径为边界节点。

　　例如，如下图所示的树。

　　按标准一打印的结果为：1，2，4，7，11，13，14，15，16，12，10，6，3

　　按标准一打印的结果为：1，2，4，7，13，14，15，16，10，6，3

 【要求】：

　　1、如果节点数为 N，两种标准实现的时间复杂度要求都为 O(N)，额外的空间复杂度要求为 O(h)，h 为二叉树的高度；

　　2、两种标准都要求逆时针顺序不重复的打印所有边界节点。

 【思路】：

　　标准一解法：打印每一层的最左节点->打印非最左最右的叶子节点->打印每一层的最右节点

　　标准二解法：第一个既有左孩子又有右孩子的节点及其这个节点前的节点全部打印->打印从这个节点开始的左边界延伸路径以及叶子节点->打印从这个节点开始的右边界的延伸路径以及叶子节点。

 

对标准一，即使不会一遍就写出很优雅的解法，至少题目是懂的，每层的最左边和最右边的节点，清晰明了。为了找出最左边和左右边的节点，书上题解用了递归的思想，先序遍历二叉树，为了保证

得到最左边和最右边的节点，采取的策略就是，最左边的节点是第一次赋值，最右边的节点是最后一次赋的值。参考setmap函数。

public static void SetMap(TreeNode node, int level, TreeNode[,] map)
        {
            if (node == null)
            {
                return;
            }

            map[level, 0] = map[level, 0] == null ? node : map[level, 0];
            map[level, 1] = node;

            SetMap(node.left, level + 1, map);

            SetMap(node.right, level + 1, map);
        }

　　

对标准二，光看题目就较难理解了。一般做算法题，题目都看不懂，手动例解不出来，还指望设计出算法来，本身就不可能了。显然，头节点和叶子节点是边界节点，无异议。

这里面剩下的两句话就不知道啥意思了，什么叫树左边界延伸下去的路径为边界节点；树右边界延伸下去的路径为边界节点。

从中文的含义来看，这是个病句。第一句主干就是说，路径是节点。这什么意思？这好比说，树是树叶一样，令人不解。

显而易见，正确理解了其中一句，另一句也就懂了。我通过例子，来说明树左边界延伸下去的路径为边界节点的意思。

 

 

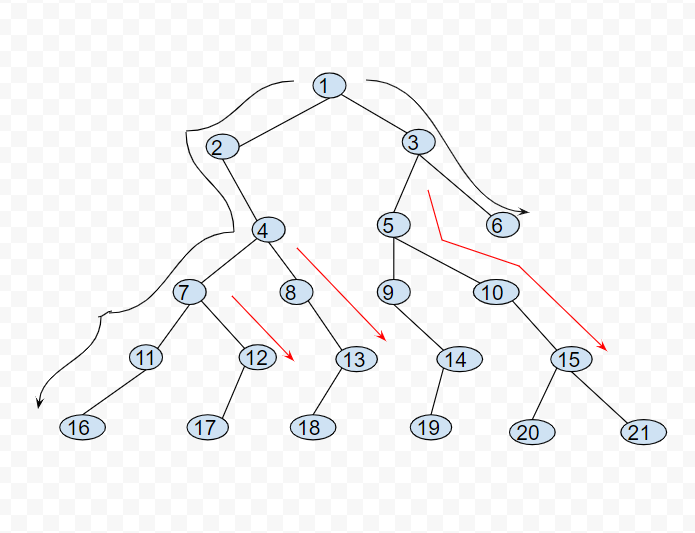
 如上图所示，黑色路径经过的节点即满足标准的节点。红色的部分，为不满足的节点。如节点8，13是节点4的右孩子， 节点12是节点7的右孩子下来路径上的节点。这些节点都不满足要求。

同理，对5，10，15还有9,14都是节点3的左孩子路径下来的节点也都不满足标准。最终满足标准的边界节点是：1,2,4,7,11,16,17,18,19,20,21,6,3,1.

static class TreeEdgePrinterS2
    {
        public static int[] PrintEdgeS2(this Tree tree)
        {
            var result = new List<int>();

            PrintEdgeS2Proc(tree.Head, result);

            return result.ToArray();

        }

        static void PrintEdgeS2Proc(TreeNode node, List<int> result)
        {
            if (node == null)
            {
                return;
            }

            result.Add(node.val);

            if (node.left != null && node.right != null)
            {
                PrintLeftEdge(node.left, true, result);
                PrintRightEdge(node.right, true, result);
            }
            else
            {
                PrintEdgeS2Proc(node.left != null ? node.left : node.right, result);
            }
        }

        static void PrintLeftEdge(TreeNode h, bool print, List<int> result)
        {
            if (h == null)
            {
                return;
            }

            if (print || (h.left == null && h.right == null))
            {
                result.Add((int)h.val);
            }

            PrintLeftEdge(h.left, print, result);

            PrintLeftEdge(h.right, print && h.left == null ? true : false, result);
        }

        static void PrintRightEdge(TreeNode h, bool print, List<int> result)
        {
            if (h == null)
            {
                return;
            }

            PrintRightEdge(h.left, print && h.right == null ? true : false, result);

            PrintRightEdge(h.right, print, result);

            if (print || (h.left == null && h.right == null))
            {
                result.Add(h.val);
            }
        }
    }