Generative Adversarial Networks 代码
GAN实现代码
数据集 :double moon dataset
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_moons import torch # 使用GPU训练,可以在菜单 "代码执行工具" -> "更改运行时类型" 里进行设置 device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") # 这是一个展示数据的函数 def plot_data(ax, X, Y, color = 'bone'): plt.axis('off') ax.scatter(X[:, 0], X[:, 1], s=1, c=Y, cmap=color) X, y = make_moons(n_samples=2000, noise=0.05) n_samples = X.shape[0] Y = np.ones(n_samples) fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9') plot_data(ax, X, Y) plt.show()

- 生成器: 32 ==> 128 ==> 2
- 判别器: 2 ==> 128 ==> 1
生成器生成一组坐标(x,y),我们希望生成器能够由一组任意的 32组噪声生成座标(x,y)处于两个半月形状上。
判别器输入的是一组座标(x,y),最后一层是sigmoid函数,是一个范围在(0,1)间的数,即样本为真或者假的置信度。如果输入的是真样本,得到的结果尽量接近1;如果输入的是假样本,得到的结果尽量接近0。
import torch.nn as nn z_dim = 32 hidden_dim = 128 # 定义生成器 net_G = nn.Sequential( nn.Linear(z_dim,hidden_dim), nn.ReLU(), nn.Linear(hidden_dim, 2)) # 定义判别器 net_D = nn.Sequential( nn.Linear(2,hidden_dim), nn.ReLU(), nn.Linear(hidden_dim,1), nn.Sigmoid()) # 网络放到 GPU 上 net_G = net_G.to(device) net_D = net_D.to(device) # 定义网络的优化器 optimizer_G = torch.optim.Adam(net_G.parameters(),lr=0.0001) optimizer_D = torch.optim.Adam(net_D.parameters(),lr=0.0001) batch_size = 50 nb_epochs = 1000 loss_D_epoch = [] loss_G_epoch = [] for e in range(nb_epochs): np.random.shuffle(X) real_samples = torch.from_numpy(X).type(torch.FloatTensor) loss_G = 0 loss_D = 0 for t, real_batch in enumerate(real_samples.split(batch_size)): # 固定生成器G,改进判别器D # 使用normal_()函数生成一组随机噪声,输入G得到一组样本 z = torch.empty(batch_size,z_dim).normal_().to(device) fake_batch = net_G(z) # 将真、假样本分别输入判别器,得到结果 D_scores_on_real = net_D(real_batch.to(device)) D_scores_on_fake = net_D(fake_batch) # 优化过程中,假样本的score会越来越小,真样本的score会越来越大,下面 loss 的定义刚好符合这一规律, # 要保证loss越来越小,真样本的score前面要加负号 # 要保证loss越来越小,假样本的score前面是正号(负负得正) loss = -torch.mean(torch.log(1-D_scores_on_fake) + torch.log(D_scores_on_real)) # 梯度清零 optimizer_D.zero_grad() # 反向传播优化 loss.backward() # 更新全部参数 optimizer_D.step() loss_D += loss # 固定判别器,改进生成器 # 生成一组随机噪声,输入生成器得到一组假样本 z = torch.empty(batch_size,z_dim).normal_().to(device) fake_batch = net_G(z) # 假样本输入判别器得到 score D_scores_on_fake = net_D(fake_batch) # 我们希望假样本能够骗过生成器,得到较高的分数,下面的 loss 定义也符合这一规律 # 要保证 loss 越来越小,假样本的前面要加负号 loss = -torch.mean(torch.log(D_scores_on_fake)) optimizer_G.zero_grad() loss.backward() optimizer_G.step() loss_G += loss if e % 50 ==0: print(f'\n Epoch {e} , D loss: {loss_D}, G loss: {loss_G}') loss_D_epoch.append(loss_D) loss_G_epoch.append(loss_G)

plt.plot(loss_D_epoch)
plt.plot(loss_G_epoch)

z = torch.empty(n_samples,z_dim).normal_().to(device) fake_samples = net_G(z) fake_data = fake_samples.cpu().data.numpy() fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9') all_data = np.concatenate((X,fake_data),axis=0) Y2 = np.concatenate((np.ones(n_samples),np.zeros(n_samples))) plot_data(ax, all_data, Y2) plt.show()
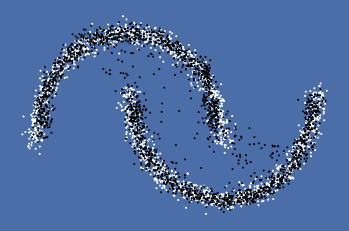
现在把学习率修改为 0.001,batch_size改大到250
# 定义网络的优化器 optimizer_G = torch.optim.Adam(net_G.parameters(),lr=0.001) optimizer_D = torch.optim.Adam(net_D.parameters(),lr=0.001) batch_size = 250 loss_D_epoch = [] loss_G_epoch = [] for e in range(nb_epochs): np.random.shuffle(X) real_samples = torch.from_numpy(X).type(torch.FloatTensor) loss_G = 0 loss_D = 0 for t, real_batch in enumerate(real_samples.split(batch_size)): # 固定生成器G,改进判别器D # 使用normal_()函数生成一组随机噪声,输入G得到一组样本 z = torch.empty(batch_size,z_dim).normal_().to(device) fake_batch = net_G(z) # 将真、假样本分别输入判别器,得到结果 D_scores_on_real = net_D(real_batch.to(device)) D_scores_on_fake = net_D(fake_batch) # 优化过程中,假样本的score会越来越小,真样本的score会越来越大,下面 loss 的定义刚好符合这一规律, # 要保证loss越来越小,真样本的score前面要加负号 # 要保证loss越来越小,假样本的score前面是正号(负负得正) loss = -torch.mean(torch.log(1-D_scores_on_fake) + torch.log(D_scores_on_real)) # 梯度清零 optimizer_D.zero_grad() # 反向传播优化 loss.backward() # 更新全部参数 optimizer_D.step() loss_D += loss # 固定判别器,改进生成器 # 生成一组随机噪声,输入生成器得到一组假样本 z = torch.empty(batch_size,z_dim).normal_().to(device) fake_batch = net_G(z) # 假样本输入判别器得到 score D_scores_on_fake = net_D(fake_batch) # 我们希望假样本能够骗过生成器,得到较高的分数,下面的 loss 定义也符合这一规律 # 要保证 loss 越来越小,假样本的前面要加负号 loss = -torch.mean(torch.log(D_scores_on_fake)) optimizer_G.zero_grad() loss.backward() optimizer_G.step() loss_G += loss if e % 50 ==0: print(f'\n Epoch {e} , D loss: {loss_D}, G loss: {loss_G}') loss_D_epoch.append(loss_D) loss_G_epoch.append(loss_G)

z = torch.empty(n_samples,z_dim).normal_().to(device) fake_samples = net_G(z) fake_data = fake_samples.cpu().data.numpy() fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9') all_data = np.concatenate((X,fake_data),axis=0) Y2 = np.concatenate((np.ones(n_samples),np.zeros(n_samples))) plot_data(ax, all_data, Y2) plt.show()

z = torch.empty(10*n_samples,z_dim).normal_().to(device) fake_samples = net_G(z) fake_data = fake_samples.cpu().data.numpy() fig, ax = plt.subplots(1, 1, facecolor='#4B6EA9') all_data = np.concatenate((X,fake_data),axis=0) Y2 = np.concatenate((np.ones(n_samples),np.zeros(10*n_samples))) plot_data(ax, all_data, Y2) plt.show();




 浙公网安备 33010602011771号
浙公网安备 33010602011771号