平衡二叉树（Balanced Binary Tree）
平衡二叉树（Balanced Binary Tree）
平衡二叉树是一种特殊的二叉搜索树，它具有以下特点：
- 每个节点的左子树和右子树的高度差不超过1。
- 所有的子树也都是平衡二叉树。
通过保持平衡性，平衡二叉树可以在最坏情况下仍然具有较好的性能，保证查找、插入和删除操作的时间复杂度为O(log n)。
平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等
为什么需要平衡二叉树
在普通的二叉搜索树中，如果插入或删除操作不经过特殊处理，很容易出现树的不平衡，使得树的高度变得很大，导致查找操作的效率下降。
平衡二叉树通过在每次插入或删除后调整树的结构，保持树的平衡性。这样可以确保树的高度尽可能地低，使得查找操作仍然可以在较短的时间内完成。
如下图：左子树全部为空，从形式上看，更像一个单链表
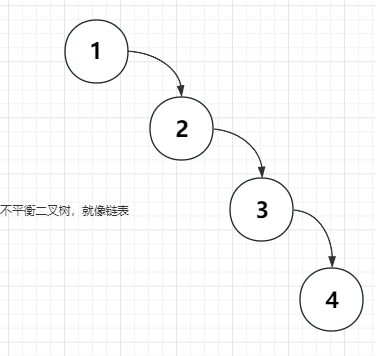
怎么平衡树高的呢？
当二叉树的左右分支树高差不为 1 时，需要进行左旋或者右旋，来调衡树高。这有点像开车的时候，如果车头偏左就往右打方向盘，车头偏右就往左打方向盘是一个道理。
class AVLTree {
private Node root;
private class Node {
int val;
int height; // 增加一个树高
Node left;
Node right;
public Node(int val) {
this.val = val;
this.height = 1;
this.left = null;
this.right = null;
}
}
}
平衡因子
平衡因子是用来衡量平衡二叉树中某个节点的左子树和右子树高度差的一个指标。它表示了节点的平衡性，可以用来判断是否需要进行旋转操作来恢复树的平衡。
平衡因子的计算方法是，对于一个节点，它的平衡因子等于左子树高度减去右子树高度。具体公式可以表示为：
平衡因子 = 左子树高度 - 右子树高度
根据平衡因子的值，可以判断节点的平衡情况：
- 平衡因子为0： 左子树和右子树的高度相等，节点处于平衡状态。
- 平衡因子为正数： 左子树的高度大于右子树的高度，节点处于左重状态。
- 平衡因子为负数： 右子树的高度大于左子树的高度，节点处于右重状态。
当平衡因子的绝对值大于1时，表示节点的左右子树高度差过大，树失去平衡，需要进行旋转操作来恢复平衡。
通过平衡因子的判断，可以及时发现不平衡的节点，并采取相应的调整措施以保持平衡二叉树的平衡性，确保树的高度在可控范围内，从而提高查找、插入和删除操作的效率。
左旋转
左旋是平衡二叉树中的一种旋转操作，用于调整不平衡节点及其子节点之间的关系。左旋的目的是将不平衡节点向左移动，并提升其右子节点作为新的父节点，从而恢复树的平衡性。
左旋的触发条件是当节点A的右子树高度较高（平衡因子大于1），并且节点B的左子树高度不小于节点B的右子树高度时，需要进行左旋操作。
具体情况下，左旋通常在以下情况下使用：
- 当在平衡二叉树中插入一个节点后，导致某个节点的平衡因子大于1，即左子树高度比右子树高度多2或更多时，需要进行左旋操作。
- 在删除节点后，导致某个节点的平衡因子小于-1，即右子树高度比左子树高度多2或更多时，也需要进行左旋操作。
左旋的目的是使得树保持平衡，确保树的高度差不超过1，从而保证查找、插入和删除等操作的时间复杂度在O(log n)范围内。
如下图：左旋的作用，相当于通过向上迁移树高差大于 1 的右子节点来降低树高的操作
- 找到需要进行左旋的节点，即节点值为4的节点。
- 将节点值为6的节点提升为新的根节点，并将原来的根节点值为4的节点降级为新根节点的左子节点。
- 将原来新根节点值为6的右子节点（值为7）作为原来根节点的右子节点。
- 将6原来的左子节点作为4个右子节点
- 更新相关节点的高度信息。
代码实现
// 左旋转操作
private Node rotateLeft(Node x) {
Node y = x.right;
Node T2 = y.left;
// 执行旋转
y.left = x;
x.right = T2;
// 更新节点高度
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
return y;
}
右旋转
和左旋转类似，目的是将不平衡节点向右移动，并提升其左子节点作为新的父节点，从而恢复树的平衡性。
- 找到需要进行右旋的节点，即节点值为10的节点。
- 将节点值为8的节点提升为新的根节点，并将原来的根节点值为10的节点降级为新根节点的右子节点。
- 将原来新根节点值为8的左子节点（值为7）作为原来根节点的左子节点。
- 更新相关节点的高度信息。
代码实现
// 右旋转操作
private Node rotateRight(Node y) {
Node x = y.left;
Node T2 = x.right;
// 执行旋转
x.right = y;
y.left = T2;
// 更新节点高度
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x;
}
左右旋（先左旋后右旋）
当某个节点的左子树的右子树过深，平衡因子小于-1时，需要进行左旋-右旋操作，先对左子节点进行左旋，然后再对当前节点进行右旋，如下图
完整代码在下面
右左旋（先右旋后左旋）
当某个节点的右子树的左子树过深，平衡因子大于1时，需要进行右旋-左旋操作，先对右子节点进行右旋，然后再对当前节点进行左旋。和上面类似
完整代码示例
public class AvlTreeDemo {
public static void main(String[] args) {
// 创建平衡二叉树对象
AVLTree avlTree = new AVLTree();
// 插入节点
avlTree.insert(10);
avlTree.insert(11);
avlTree.insert(7);
avlTree.insert(6);
avlTree.insert(8);
avlTree.insert(9);
// 中序遍历并输出节点值
System.out.print("中序遍历结果：");
avlTree.inorderTraversal(); // 输出：10 20 25 30 40 50
}
}
class AVLTree {
private Node root;
private class Node {
int val;
int height;
Node left;
Node right;
public Node(int val) {
this.val = val;
this.height = 1;
this.left = null;
this.right = null;
}
}
// 计算节点的高度
private int height(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 计算节点的平衡因子
private int balanceFactor(Node node) {
if (node == null) {
return 0;
}
return height(node.left) - height(node.right);
}
// 右旋转操作
private Node rotateRight(Node y) {
Node x = y.left;
Node T2 = x.right;
// 执行旋转
x.right = y;
y.left = T2;
// 更新节点高度
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x;
}
// 左旋转操作
private Node rotateLeft(Node x) {
Node y = x.right;
Node T2 = y.left;
// 执行旋转
y.left = x;
x.right = T2;
// 更新节点高度
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
return y;
}
// 插入节点
public void insert(int val) {
root = insertNode(root, val);
}
private Node insertNode(Node node, int val) {
// 执行标准的BST插入
if (node == null) {
return new Node(val);
}
if (val < node.val) {
node.left = insertNode(node.left, val);
} else if (val > node.val) {
node.right = insertNode(node.right, val);
} else { // 如果值相等，不允许重复插入
return node;
}
// 更新节点的高度
node.height = Math.max(height(node.left), height(node.right)) + 1;
// 计算平衡因子
int balance = balanceFactor(node);
// 进行平衡调整
// 左子树不平衡，右旋转
if (balance > 1 && val < node.left.val) {
return rotateRight(node);
}
// 右子树不平衡，左旋转
if (balance < -1 && val > node.right.val) {
return rotateLeft(node);
}
// 左子树不平衡，先左旋转后右旋转
if (balance > 1 && val > node.left.val) {
node.left = rotateLeft(node.left);
return rotateRight(node);
}
// 右子树不平衡，先右旋转后左旋转
if (balance < -1 && val < node.right.val) {
node.right = rotateRight(node.right);
return rotateLeft(node);
}
return node;
}
// 中序遍历
public void inorderTraversal() {
inorderHelper(root);
}
private void inorderHelper(Node node) {
if (node == null) {
return;
}
inorderHelper(node.left);
System.out.print(node.val + " ");
inorderHelper(node.right);
}
public static void main(String[] args) {
// 创建平衡二叉树对象
AVLTree avlTree = new AVLTree();
// 插入节点
avlTree.insert(10);
avlTree.insert(20);
avlTree.insert(30);
avlTree.insert(40);
avlTree.insert(50);
avlTree.insert(25);
// 中序遍历并输出节点值
System.out.print("中序遍历结果：");
avlTree.inorderTraversal(); // 输出：10 20 25 30 40 50
}
}
