红黑树简介
红黑树是一种搜索二叉树,而且也是一种平衡搜索二叉树,它可以保证在最坏的情况下的基本的操作的时间复杂度为O(lgn)。
红黑树具有如下的性质:
- 每个节点要么是红色的,要不是黑色的。
- 根节点是黑色的
- 每个叶节点(NIL)是黑色的
- 如果一个结点是红色的,则它的两个子结点是黑色的。
- 对每个节点,从该节点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
红黑树的旋转
注意这个旋转和AVL树的旋转不一样,红黑树的旋转只有左旋和右旋。那为什么要旋转呢,因为是在插入和删除节点后,这棵树可能就不满足红黑树的性质了,所以需要做一些重新着色和旋转的操作。
下面看一下左旋和右旋的示意图。
左旋可以理解为,以那个节点左旋的,这个节点就会成为自己右孩子的左孩子。
右旋可以理解为,以那个节点右旋的,这个节点就会成为自己左孩子的右孩子。
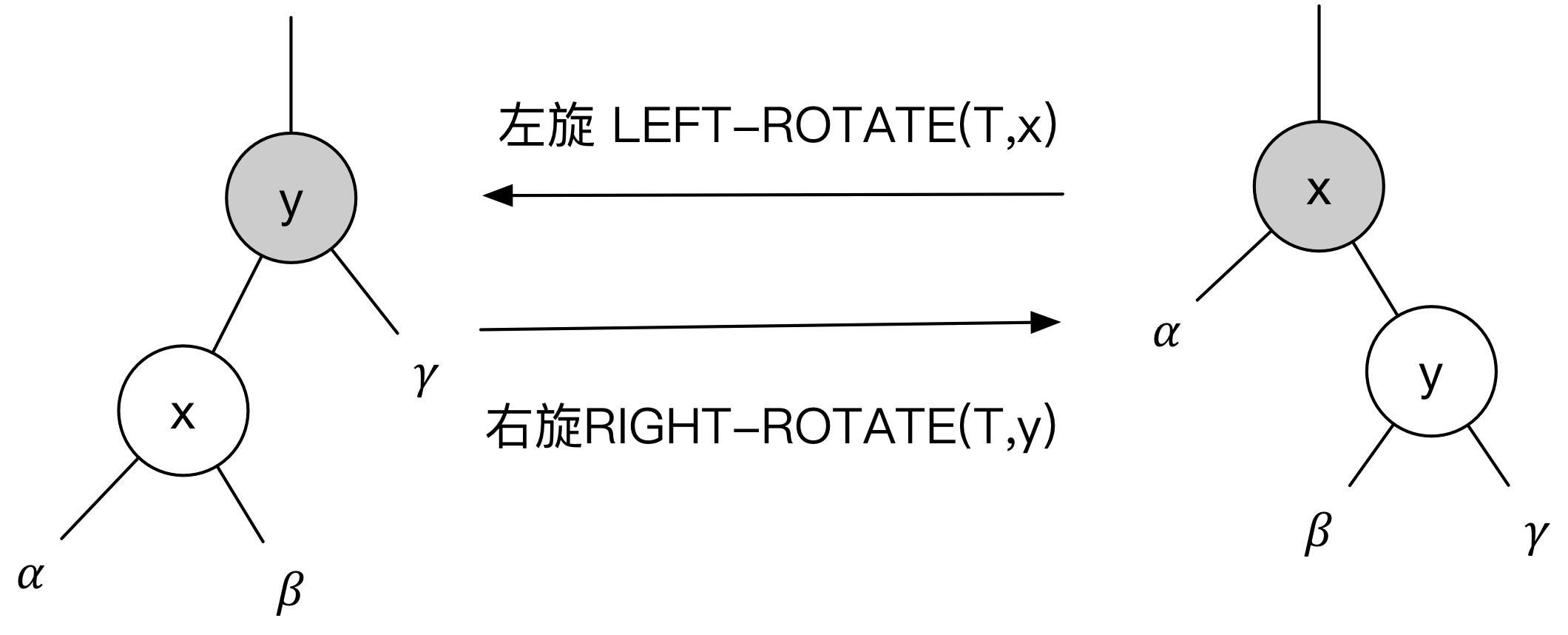
下面是左旋的伪代码 假设 x.right !=T.nil 且根结点的父结点为T.nil
LEFT-ROTATE(T, x) y = x.right // x的右孩子为y x.right = y.left // 将 “y的左孩子” 设为 “x的右孩子”,即 将β设为x的右孩子 if y.left != T.nil // 将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为x y.left.p = x y.p = x.p // 将 “x的父亲” 设为 “y的父亲”
if x.p == T.nil // 如果x的父亲为null,所以x节点是根节点,这时就把y设为根节点
T.root = y
elseif x == x.p.left // 如果x是父节点的左孩子,就把y设置x父节点的左孩子
x.p.left = y
else x.p.right = y // 如果x是父节点的右孩子,就把y设置x父节点的右孩子
y.left = x // 把x设置为y的左孩子,
x.p = y // 把y设为x的父亲
右旋的伪代码
RIGHT-ROTATE(T, y) x = y.left // y的左孩子为x y.left = x.right // 将 “x的右孩子” 设为 “y的左孩子”,即 将β设为x的右孩子 if x.right != T.nil // 将 “y” 设为 “x的右孩子的父亲”,即 将β的父亲设为y x.right.p = y x.p = y.p // 将 “y的父亲” 设为 “x的父亲” if y.p == T.nil // 如果y的父亲为null,所以y节点是根节点,这时就把x设为根节点 T.root = x elseif y == y.p.left // 如果y是父节点的左孩子,就把x设置y父节点的左孩子 y.p.left = x else y.p.right = x // 如果y是父节点的右孩子,就把x设置y父节点的右孩子 x.left = y // 把y设置为x的右孩子, y.p = x // 把x设为y的父亲
红黑树的插入
红黑树的插入前面的逻辑和普通的二叉搜索树的插入逻辑差不多。这里不再多说,主要差别在于插入后可能会破坏红黑树的性质。我们主要来看看修复的伪代码。
先把要插入节点设为红色,为什么设为红色而不是黑色呢,这个可以先看一下红黑树的性质,如果把插入节点设置黑色,那么性质1234都不违背,但是性质5肯定违背。如果设置为红色呢,则可能违背2和4,注意是可能。也有可能插入的红色节点后,依然是一个红黑树。
1 如果插入的节点是根节点。则把节点颜色从红色变为黑色即可。
2 如果插入的节点不是根节点,但是待插入位置的父节点是黑色。插入红色节点不会违背任何红黑树性质。
3 如果不是上面两种情况,则情况要复杂了。分为三种情况处理。下面先看一下伪代码。
RB-INSERT-FIXUP(T, z) while z.p.color == RED // 若“当前节点(z)的父节点是红色”,则进行以下处理。 if z.p == z.p.p.left // 若“z的父节点”是“z的祖父节点的左孩子”,则进行以下处理。 y = z.p.p.right // 将y设置为“z的叔叔节点(z的祖父节点的右孩子)” if y.color == RED // Case 1条件:叔叔是红色 z.p.color = BLACK ▹ Case 1 // (01) 将“父节点”设为黑色。 y.color = BLACK ▹ Case 1 // (02) 将“叔叔节点”设为黑色。 z.p.p.color = RED ▹ Case 1 // (03) 将“祖父节点”设为“红色”。 z = z.p.p ▹ Case 1 // (04) 将“祖父节点”设为“当前节点”(红色节点) else if z == z.p.right // Case 2条件:叔叔是黑色,且当前节点是右孩子 z = z.p ▹ Case 2 // (01) 将“父节点”作为“新的当前节点”。 LEFT-ROTATE(T, z) ▹ Case 2 // (02) 以“新的当前节点”为支点进行左旋。 z.p.color = BLACK ▹ Case 3 // Case 3条件:叔叔是黑色,且当前节点是左孩子。(01) 将“父节点”设为“黑色”。 z.p.p.color = RED ▹ Case 3 // (02) 将“祖父节点”设为“红色”。 RIGHT-ROTATE(T, z.p.p) ▹ Case 3 // (03) 以“祖父节点”为支点进行右旋。 else (same as then clause with "right" and "left" exchanged) // 若“z的父节点”是“z的祖父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 T.root.color = BLACK
RB-INSERT-FIXUP(T, z) while z.p.color == RED // 若“当前节点(z)的父节点是红色”,则进行以下处理。 if z.p = z.p.p.right // 若“z的父节点”是“z的祖父节点的右孩子”,则进行以下处理。 y = z.p.p.left // 将y设置为“z的叔叔节点(z的祖父节点的左孩子)” if y.color == RED // Case 1条件:叔叔是红色 z.p.color = BLACK ▹ Case 1 // (01) 将“父节点”设为黑色。 y.color = BLACK ▹ Case 1 // (02) 将“叔叔节点”设为黑色。 z.p.p.color = RED ▹ Case 1 // (03) 将“祖父节点”设为“红色”。 z = z.p.p ▹ Case 1 // (04) 将“祖父节点”设为“当前节点”(红色节点) else if z == z.p.left // Case 2条件:叔叔是黑色,且当前节点是左孩子 z = z.p ▹ Case 2 // (01) 将“父节点”作为“新的当前节点”。 RIGHT-ROTATE(T, z) ▹ Case 2 // (02) 以“新的当前节点”为支点进行右旋。 z.p.color = BLACK ▹ Case 3 // Case 3条件:叔叔是黑色,且当前节点是右孩子。(01) 将“父节点”设为“黑色”。 z.p.p.color = RED ▹ Case 3 // (02) 将“祖父节点”设为“红色”。 LEFT-ROTATE(T, z.p.p) ▹ Case 3 // (03) 以“祖父节点”为支点进行左旋。 else (same as then clause with "right" and "left" exchanged) // 若“z的父节点”是“z的祖父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 T.root.color = BLACK
1 当父节点是祖父节点的左孩子时
| 条件 | 处理策略 | |
| case1 | 父节点是红色,叔叔节点红色 |
1 将父节点设置黑色 2 将叔叔节点设置黑色 3 将祖父节点设置红色 4将祖父节点设为当前节点继续 |
| case2 | 父节点是红色,叔叔是黑色,且当前节点是右孩子 |
1 将“父节点”作为“新的当前节点”。 2 以“新的当前节点”为支点进行左旋 |
| case3 | 父节点是红色,叔叔是黑色,且当前节点是左孩子 |
1 以“新的当前节点”将“父节点”设为“黑色” 2 将“祖父节点”设为“红色” 3 以“祖父节点”为支点进行右旋 |
2 当父节点是祖父节点的右孩子时
| 条件 |
处理策略 |
|
| case1 | 父节点是红色,叔叔节点红色 |
1 将父节点设置黑色 2 将叔叔节点设置黑色 3 将祖父节点设置红色 4将祖父节点设为当前节点继续 |
| case2 | 父节点是红色,叔叔是黑色,且当前节点是右孩子 |
1 将“父节点”作为“新的当前节点”。 2 以“新的当前节点”为支点进行右旋 |
| case3 | 父节点是红色,叔叔是黑色,且当前节点是左孩子 |
1 以“新的当前节点”将“父节点”设为“黑色” 2 将“祖父节点”设为“红色” 3 以“祖父节点”为支点进行左旋 |
这就是所有的关于红黑树的应对情况。其实不用太紧张,这就像是公式一样,遇到什么情况,做什么操作是一定的。所以不太明白的话,就动手做几遍。就会加深理解了,
红黑树的删除
删除操作相对于插入要更复杂一些。想像一下,在二叉树删除时,我们分为三种情况,删除节点只有左孩子,删除节点只有右孩子,删除节点有两个孩子的情况,其中删除节点有两个孩子节点的时候,需要找出
删除节点的后继节点,这时后继节点肯定只有右孩子,把后继节点移到待删除的节点,其实就相当于删除了后继节点。然后删除又转化为只有右孩子的情况。
而红黑树的删除只是在这个情况上,多了一个颜色属性,还有删除可能违背红黑树的性质,那什么情况下删除节点会违背红黑树的性质呢。当删除的节点颜色是黑色的时候,会违背红黑树的性质。
为什么删除红色节点不会违背呢,
那就看看红黑树的性质,看看会不会违背吧,性质1肯定不会,因为删除前是一个红黑树,删除节点肯定不会破坏这个性质,因为删除的节点的红色的,所以删除的节点不是根节点,根节点依然是黑色的。性质3也肯定不会违背了。
性质4,也不会,因为删除的红色节点,所以删除节点的子节点和父节点都是黑色的。性质5也不会,因为删除的是红色节点。不会影响每条路径上黑色节点的数目。
那么删除节点为黑色有分为那些情况呢,
1 当删除的节点为根节点时,如果是它的红色孩子节点移到根节点,这时只要把节点置为黑色即可,
2 当删除节点不是根节点。那么如果它的孩子节点是红色的,这时也是只要把节点置为黑色即可。
如果不是以上两种情况,就有点复杂了,先看下面的伪代码。
RB-DELETE-FIXUP(T, x) while x ≠ T.root and x.color == BLACK if x == x.p.left // 如果x是它父亲的左孩子 w = x.p.right // 若 “x”是“它父节点的左孩子”,则设置 “w”为“x的兄弟”(即w为x父节点的右孩子) if w.color == RED // Case 1: x是“黑+黑”节点,x的兄弟是红色。(此时x的父节点和x的叔叔节点的子节点都是黑节点)。 w.color = BLACK ▹ Case 1 // (01) 将x的兄弟节点设为“黑色”。 x.p.color = RED ▹ Case 1 // (02) 将x的父节点设为“红色”。 LEFT-ROTATE(T, x.p) ▹ Case 1 // (03) 对x的父节点进行左旋。 w = x.p.right ▹ Case 1 // (04) 左旋后,重新设置x的兄弟节点。 if w.left.color == BLACK and w.right.color == BLACK // Case 2: x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。 w.color = RED ▹ Case 2 // (01) 将x的兄弟节点设为“红色”。 x = x.p ▹ Case 2 // (02) 设置“x的父节点”为“新的x节点”。 else if w.right.color == BLACK // Case 3: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。 w.left.color = BLACK ▹ Case 3 // (01) 将x兄弟节点的左孩子设为“黑色”。 w.color = RED ▹ Case 3 // (02) 将x兄弟节点设为“红色”。 RIGHT-ROTATE(T, w) ▹ Case 3 // (03) 对x的兄弟节点进行右旋。 w = x.p.right ▹ Case 3 // (04) 右旋后,重新设置x的兄弟节点。 w.color = x.p.color ▹ Case 4 // Case 4: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的。(01) 将x父节点颜色 赋值给 x的兄弟节点。 x.p.color = BLACK ▹ Case 4 // (02) 将x父节点设为“黑色”。 w.right.color = BLACK ▹ Case 4 // (03) 将x兄弟节点的右子节设为“黑色”。 LEFT-ROTATE(T, x.p) ▹ Case 4 // (04) 对x的父节点进行左旋。 x = T.root ▹ Case 4 // (05) 设置“x”为“根节点”。 else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 x.color = BLACK
RB-DELETE-FIXUP(T, x) while x ≠ T.root and x.color == BLACK if x == x.p.right // 如果x是它父亲的右孩子 w = x.p.left // 若 “x”是“它父节点的右孩子”,则设置 “w”为“x的兄弟”(即w为x父节点的左孩子) if w.color == RED // Case 1: x是“黑+黑”节点,x的兄弟是红色。(此时x的父节点和x的叔叔节点的子节点都是黑节点)。 w.color = BLACK ▹ Case 1 // (01) 将x的兄弟节点设为“黑色”。 x.p.color = RED ▹ Case 1 // (02) 将x的父节点设为“红色”。 RIGHT-ROTATE(T, x.p) ▹ Case 1 // (03) 对x的父节点进行右旋。 w = x.p.left ▹ Case 1 // (04) 右旋后,重新设置x的兄弟节点。 if w.left.color == BLACK and w.right.color == BLACK // Case 2: x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。 w.color = RED ▹ Case 2 // (01) 将x的兄弟节点设为“红色”。 x = x.p ▹ Case 2 // (02) 设置“x的父节点”为“新的x节点”。 else if w.left.color == BLACK // Case 3: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色,左孩子是黑色的。 w.right.color = BLACK ▹ Case 3 // (01) 将x兄弟节点的右孩子设为“黑色”。 w.color = RED ▹ Case 3 // (02) 将x兄弟节点设为“红色”。 LEFT-ROTATE(T, w) ▹ Case 3 // (03) 对x的兄弟节点进行左旋。 w = x.p.left ▹ Case 3 // (04) 左旋后,重新设置x的兄弟节点。 w.color = x.p.color ▹ Case 4 // Case 4: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色的。(01) 将x父节点颜色 赋值给 x的兄弟节点。 x.p.color = BLACK ▹ Case 4 // (02) 将x父节点设为“黑色”。 w.left.color = BLACK ▹ Case 4 // (03) 将x兄弟节点的左子节设为“黑色”。 RIGHT-ROTATE(T, x.p) ▹ Case 4 // (04) 对x的父节点进行右旋。 x = T.root ▹ Case 4 // (05) 设置“x”为“根节点”。 else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父节点的左孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 x.color = BLACK
前提条件 x节点不是根节点,并且x的颜色是红色的。并且x是父节点的左孩子
| 条件 |
处理策略 |
|
| case1 | 兄弟节点是红色的 |
1 将x的兄弟节点设为黑色。 2 将x的父节点设为红色。 3 对x的父节点进行左旋。 4 左旋后,重新设置x的兄弟节点。 |
| case2 | x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色 |
1 将x的兄弟节点设为红色。 2 设置“x的父节点”为“新的x节点”。 |
| case3 | x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。 |
1 将x兄弟节点的左孩子设为“黑色”。 2 将x兄弟节点设为红色。 3 对x的兄弟节点进行右旋。 4 右旋后,重新设置x的兄弟节点。 |
| case4 | x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。 |
1 将x父节点颜色 赋值给 x的兄弟节点。 2 将x父节点设为“黑色”。 3 将x兄弟节点的右子节设为“黑色”。 4 对x的父节点进行左旋。 5 设置“x”为“根节点”。 |
前提条件 x节点不是根节点,并且x的颜色是红色的。并且x是父节点的右孩子
| 条件 |
处理策略 |
|
| case1 | 兄弟节点是红色的 |
1 将x的兄弟节点设为黑色。 2 将x的父节点设为红色。 3 对x的父节点进行右旋。 4 右旋后,重新设置x的兄弟节点。 |
| case2 | x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色 |
1 将x的兄弟节点设为红色。 2 设置“x的父节点”为“新的x节点”。 |
| case3 | x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。 |
1 将x兄弟节点的右孩子设为“黑色”。 2 将x兄弟节点设为红色。 3 对x的兄弟节点进行左旋。 4 左旋后,重新设置x的兄弟节点。 |
| case4 | x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。 |
1 将x父节点颜色 赋值给 x的兄弟节点。 2 将x父节点设为“黑色”。 3 将x兄弟节点的左子节设为“黑色”。 4 对x的父节点进行右旋。 5 设置“x”为“根节点”。 |
JAVA版本实现
package cn.damai.maitix.tic.devut.service; /** * Created by dupang on 2017/11/12. */ public class RBTreeNode<T> { /** * 节点的左孩子 */ private RBTreeNode<T> left; /** * 节点的右孩子 */ private RBTreeNode<T> right; /** * 节点的父亲 */ private RBTreeNode<T> parent; /** * 节点的颜色 */ private Boolean color ; /** * 节点的值 */ private T value; public RBTreeNode() { } public RBTreeNode(RBTreeNode<T> left, RBTreeNode<T> right, RBTreeNode<T> parent, T value, Boolean color) { this.left = left; this.right = right; this.parent = parent; this.value = value; this.color = color; } public RBTreeNode<T> getLeft() { return left; } public void setLeft(RBTreeNode<T> left) { this.left = left; } public RBTreeNode<T> getRight() { return right; } public void setRight(RBTreeNode<T> right) { this.right = right; } public RBTreeNode<T> getParent() { return parent; } public void setParent(RBTreeNode<T> parent) { this.parent = parent; } public T getValue() { return value; } public void setValue(T value) { this.value = value; } public Boolean getColor() { return color; } public void setColor(Boolean color) { this.color = color; } @Override public boolean equals(Object o) { if (this == o) { return true; } if (o == null || getClass() != o.getClass()) { return false; } RBTreeNode<?> that = (RBTreeNode<?>)o; if (left != null ? !left.equals(that.left) : that.left != null) { return false; } if (right != null ? !right.equals(that.right) : that.right != null) { return false; } if (parent != null ? !parent.equals(that.parent) : that.parent != null) { return false; } if (color != null ? !color.equals(that.color) : that.color != null) { return false; } return value != null ? value.equals(that.value) : that.value == null; } @Override public int hashCode() { int result = left != null ? left.hashCode() : 0; result = 31 * result + (right != null ? right.hashCode() : 0); result = 31 * result + (parent != null ? parent.hashCode() : 0); result = 31 * result + (color != null ? color.hashCode() : 0); result = 31 * result + (value != null ? value.hashCode() : 0); return result; } }
测试类
package cn.damai.maitix.tic.devut.service; /** * Created by dupang on 2017/11/12. */ public class RBTreeTest { private static final Boolean RED = true; private static final Boolean BLACK = false; private static final RBTreeNode<Integer> NULL_NODE = new RBTreeNode<>(null, null, null, null, BLACK); public static void main(String[] args) { int[] values = new int[] {18, 5, 3, 9, 2, 13, 32}; //初始化一个表示树的根节点 RBTreeNode<Integer> root = new RBTreeNode<>(NULL_NODE, NULL_NODE, NULL_NODE, null, BLACK); //遍历插入 for (Integer value : values) { //初始化要插入的节点 RBTreeNode<Integer> treeNode = new RBTreeNode<>(NULL_NODE, NULL_NODE, NULL_NODE, value, RED); RBTreeNode<Integer> treeNode2 = new RBTreeNode<>(NULL_NODE, NULL_NODE, NULL_NODE, value, RED); System.out.println(treeNode == treeNode2); rbInsert(root, treeNode); } //中序遍历 inOrderTreeWalk(root); System.out.println(); //先序遍历 preOrderTreeWalk(root); System.out.println(); //后序遍历 postOrderTreeWalk(root); System.out.println(); RBTreeNode<Integer> treeNode = treeSearch(root,3); //求最大值 treeMaximum(root); //求最小值 treeMinimum(root); //后继 treeSuccessor(root); //前驱 treePredecessor(root); } /** * 红黑树的插入操作 * * @param root 二叉树的根 * @param z 要插入的节点 */ public static void rbInsert(RBTreeNode<Integer> root, RBTreeNode<Integer> z) { //声明一个y,用于记录while循环中循环节点的位置,也就是插入节点要插入的位置 RBTreeNode<Integer> y = NULL_NODE; //把树的根节点赋值给x,先从根节点开始寻找插入的点。 RBTreeNode<Integer> x = root; while (!NULL_NODE.equals(x)) { y = x; //如果要插入的值比根节点的值大, if (z.getValue() > x.getValue()) { x = x.getRight(); } else { x = x.getLeft(); } } z.setParent(y); // y是最后找到的插入的位置,就把z的父亲设为y。 //如果y是null,说明是个空树 if (y.equals(NULL_NODE)) { z.setParent(null); z.setLeft(null); z.setRight(null); z.setValue(z.getValue()); z.setColor(BLACK); } else if (z.getValue() < y.getValue()) { //如果插入的节点比y小,就把y的左孩子设为z y.setLeft(z); } else { //如果插入的节点比y大,就把y的右孩子设为z y.setRight(z); } z.setColor(RED); //把插入的节点颜色设为红色 rbInsertFixup(root, z); //因为插入节点后可能破坏红黑树的性质,所以调用这个方法来修正使基再次成为红黑树 } /** * 插入后修正红黑树 * * @param root 根节点 * @param z 当前节点 */ public static void rbInsertFixup(RBTreeNode<Integer> root, RBTreeNode<Integer> z) { while (z.getParent().getColor() == RED) { if (z.getParent() == z.getParent().getParent().getLeft()) { //如果插入节点的父节点是祖父节点的左孩子 RBTreeNode<Integer> y = z.getParent().getParent().getRight(); //y是z的叔叔节点 if (y.getColor() == RED) { //case 1 如果叔叔节点的颜色是红色的 z.getParent().setColor(BLACK); //case 1 把z的父节点设为黑色 y.setColor(BLACK); //case 1 把叔叔节点设为黑色 z.getParent().getParent().setColor(RED); //case 1 把祖父节点设为红色 z = z.getParent().getParent(); //case 1 把祖父节点设置为当前节点继续操作 } else { if (z == z.getParent().getRight()) { //case 2 如果z是之父节点的右孩子 z = z.getParent(); //case 2 把父节点设为当前节点继续操作 leftRotate(root, z); //case 2 把父节点设为当前节点进行左旋 } z.getParent().setColor(BLACK); //case 3 设置父节点的颜色为黑色 z.getParent().getParent().setColor(RED); //case 3 设置祖父节点的颜色为红色 rightRotate(root, z.getParent().getParent()); //case 3 把祖父节点设为当前节点进行右旋 } } else { //如果插入节点的父节点是祖父节点的右孩子 RBTreeNode<Integer> y = z.getParent().getParent().getLeft(); //y是z的叔叔节点 if (y.getColor() == RED) { //case 1 如果叔叔节点的颜色是红色的 z.getParent().setColor(BLACK); //case 1 把z的父节点设为黑色 y.setColor(BLACK); //case 1 把叔叔节点设为黑色 z.getParent().getParent().setColor(RED); //case 1 把祖父节点设为红色 z = z.getParent().getParent(); //case 1 把祖父节点设置为当前节点继续操作 } else { if (z == z.getParent().getLeft()) { //case 2 如果z是之父节点的左孩子 z = z.getParent(); //case 2 把父节点设为当前节点继续操作 rightRotate(root, z); //case 2 把父节点设为当前节点进行右旋 } z.getParent().setColor(BLACK); //case 3 设置父节点的颜色为黑色 z.getParent().getParent().setColor(RED); //case 3 设置祖父节点的颜色为红色 leftRotate(root, z.getParent().getParent()); //case 3 把祖父节点设为当前节点进行左旋 } } } } /** * 左旋 * * @param root 根节点 * @param x 旋转的节点 */ public static void leftRotate(RBTreeNode<Integer> root, RBTreeNode<Integer> x) { RBTreeNode<Integer> y = x.getRight(); //假设x的右孩子是y x.setRight(y.getLeft()); // y的左孩子变为x的右孩子 if (!NULL_NODE.equals(y.getLeft())) { // 如果y的左孩子不为null,就设置它的父节点为x y.getLeft().setParent(x); } y.setParent(x.getParent()); //把y的父节点换为x的父节点 if (NULL_NODE.equals(x.getParent())) { //如果x的父节点为null,说明x是根节点,就把y设置为根节点。 y.setParent(root.getParent()); y.setRight(root.getRight()); y.setLeft(root.getLeft()); y.setColor(root.getColor()); y.setValue(root.getValue()); } else if (x == x.getParent().getLeft()) { //如果x是其父节点的左孩子,就设置x的父节点的左孩子为y x.getParent().setLeft(y); } else { x.getParent().setRight(y); //如果x是其父节点的右孩子,就设置x的父节点的右孩子为y } y.setLeft(x); //设置y的左孩子为x x.setParent(y); //设置x的父亲为y } /** * 右旋 * * @param root 根节点 * @param y 旋转的节点 */ public static void rightRotate(RBTreeNode<Integer> root, RBTreeNode<Integer> y) { RBTreeNode<Integer> x = y.getLeft(); //假设y的左孩子是x y.setLeft(x.getRight()); // y的左孩子变为x的右孩子 if (!NULL_NODE.equals(x.getRight())) { // 如果y的左孩子不为null,就设置它的父节点为x x.getRight().setParent(y); } x.setParent(y.getParent()); //把y的父节点换为x的父节点 if (x.getRight().equals(y.getParent())) { //如果y的父节点为null,说明y是根节点,就把x设置为根节点。 x.setParent(root.getParent()); x.setRight(root.getRight()); x.setLeft(root.getLeft()); x.setColor(root.getColor()); x.setValue(root.getValue()); } else if (y == y.getParent().getLeft()) { //如果y是其父节点的左孩子,就设置y的父节点的左孩子为x y.getParent().setLeft(x); } else { y.getParent().setRight(x); //如果y是其父节点的右孩子,就设置y的父节点的右孩子为x } x.setRight(y); //设置x的左孩子为y y.setParent(x); //设置y的父亲为x } /** * 中序遍历 * * @param treeNode 根节点 */ public static void inOrderTreeWalk(RBTreeNode<Integer> treeNode) { if (!NULL_NODE.equals(treeNode)) { inOrderTreeWalk(treeNode.getLeft()); System.out.print(treeNode.getValue() + " "); inOrderTreeWalk(treeNode.getRight()); } } /** * 前序遍历 * * @param treeNode 根节点 */ public static void preOrderTreeWalk(RBTreeNode<Integer> treeNode) { if (treeNode != null && treeNode.getValue() != null) { System.out.print(treeNode.getValue() + " "); inOrderTreeWalk(treeNode.getLeft()); inOrderTreeWalk(treeNode.getRight()); } } /** * 后序遍历 * * @param treeNode 根节点 */ public static void postOrderTreeWalk(RBTreeNode<Integer> treeNode) { if (!NULL_NODE.equals(treeNode)) { inOrderTreeWalk(treeNode.getLeft()); inOrderTreeWalk(treeNode.getRight()); System.out.print(treeNode.getValue() + " "); } } /** * 在树中查询指定值的节点 * * @param treeNode 树的节点 * @param k 要查询的值 * @return 如果查询到节点的值等于要查询的值,就返回这个节点,否则返回null */ public static RBTreeNode<Integer> treeSearch(RBTreeNode<Integer> treeNode, Integer k) { if (NULL_NODE.equals(treeNode) || treeNode.getValue() == k) { return treeNode; } if (k > treeNode.getValue()) { return treeSearch(treeNode.getRight(), k); } else { return treeSearch(treeNode.getLeft(), k); } } /** * 在树中找到最大值 * * @param treeNode 树的节点 * @return 如果查询到节点的值等于要查询的值,就返回这个节点,否则返回null */ public static RBTreeNode<Integer> treeMaximum(RBTreeNode<Integer> treeNode) { while (!NULL_NODE.equals(treeNode.getRight())) { treeNode = treeNode.getRight(); } return treeNode; } /** * 在树中找到最小值 * * @param treeNode 树的节点 * @return 如果查询到节点的值等于要查询的值,就返回这个节点,否则返回null */ public static RBTreeNode<Integer> treeMinimum(RBTreeNode<Integer> treeNode) { while (!NULL_NODE.equals(treeNode.getLeft())) { treeNode = treeNode.getLeft(); } return treeNode; } /** * 找一个节点的后继 * * @return 一个节点的后继 */ public static RBTreeNode<Integer> treeSuccessor(RBTreeNode<Integer> treeNode) { if (!NULL_NODE.equals(treeNode.getRight())) { return treeMinimum(treeNode.getRight()); } RBTreeNode<Integer> y = treeNode.getParent(); while (y != null && treeNode == y.getRight()) { treeNode = y; y = y.getParent(); } return y; } /** * 找一个节点的前驱 * * @return 一个节点的前驱 */ public static RBTreeNode<Integer> treePredecessor(RBTreeNode<Integer> treeNode) { if (!NULL_NODE.equals(treeNode.getLeft())) { return treeMaximum(treeNode.getLeft()); } RBTreeNode<Integer> y = treeNode.getParent(); while (y != null && treeNode == y.getLeft()) { treeNode = y; y = y.getParent(); } return y; } public static void transplant(RBTreeNode<Integer> root, RBTreeNode<Integer> target, RBTreeNode<Integer> source) { if (target.getParent() == null) { root.setValue(source.getValue()); root.setLeft(source.getLeft()); root.setRight(source.getRight()); root.setParent(source.getParent()); root.setColor(BLACK); } else if (target == target.getParent().getLeft()) { target.getParent().setLeft(source); } else { target.getParent().setRight(source); } source.setParent(target.getParent()); } /** * 从一棵树中删除一个节点 * * @param root 根节点 * @param z 要删除的节点 */ public static void treeDelete(RBTreeNode<Integer> root, RBTreeNode<Integer> z) { RBTreeNode<Integer> y = z; // 记录要删除的节点 Boolean yOriginalColor = y.getColor(); // 记录删除节点的原来的颜色 RBTreeNode<Integer> x; // x是y的右孩子 if (NULL_NODE.equals(z.getLeft())) { // 如果z的左孩子为空 x = z.getRight(); // 就把z的右孩子直接替换z transplant(root, z, z.getRight()); } else if (NULL_NODE.equals(z.getRight())) { // 如果z的右孩子为空 x = z.getLeft(); // 就把z的左孩子直接替换z transplant(root, z, z.getLeft()); } else { y = treeMinimum(z.getRight()); // 如果z的两个孩子都不为空 就找到z的后继t yOriginalColor = y.getColor(); // 重新记录z的后继y的颜色 x = y.getRight(); // 重新记录y的右孩子 if (y.getParent() == z) { // 如果后继y是z的孩子,就把y的右孩子的父亲设为y, x.setParent(y); // 其实这一步感觉没必要。x本来是y的右孩子,肯定x的父亲是y } else { // transplant(root, y, y.getRight()); // 先用y的右孩子替换y y.setRight(z.getRight()); // 把y的右孩子设为z的右孩子 y.getRight().setParent(y); // 把y新的右孩子的父亲设为y } transplant(root, z, y); // 用y替换z y.setLeft(z.getLeft()); // 把y的左孩子设为z的左孩子 y.getLeft().setParent(y); // 把y新的左孩子的父节点设为y y.setColor(z.getColor()); // 把y的颜色设置为z的颜色 } if (yOriginalColor == BLACK) { // 如果要删除的节点的颜色是黑色的,就破坏了红黑树的 rbDeleteFixup(root, x); // 性质,需要进行修正 } } /** * 红黑树删除后的修正 * * @param root 根节点 * @param x 删除节点的右孩子 */ public static void rbDeleteFixup(RBTreeNode<Integer> root, RBTreeNode<Integer> x) { while (x != root && x.getColor() == BLACK) { if (x == x.getParent().getLeft()) { // 如果x是其父节点的左孩子 RBTreeNode<Integer> w = x.getParent().getRight(); // w是x的兄弟节点 if (w.getColor() == RED) { // case1 如果x的兄弟节点是红色的 w.setColor(BLACK); // case1 设兄弟节点w的颜色为黑色 x.getParent().setColor(RED); // case1 设x父节点的颜色为红色 leftRotate(root, x.getParent()); // case1 以x的父节点左旋 w = x.getParent().getRight(); // case1 重新设置x的兄弟节点w } if (w.getLeft().getColor() == BLACK && w.getRight().getColor() == BLACK) { // case2 如果兄弟节点w的左右孩子颜色都是黑色 w.setColor(RED); // case2 设兄弟节点w的颜色为红色 x = x.getParent(); // case2 设x的父节点为当前节点 } else { if (w.getRight().getColor() == BLACK) { // case3 如果兄弟节点w的右孩子是黑色 w.getLeft().setColor(BLACK); // case3 设兄弟节点w的左孩子是黑色 w.setColor(RED); // case3 设兄弟节点w的颜色是红色 rightRotate(root, w); // case3 右旋兄弟节点w w = x.getParent().getRight(); // case3 重新设置x的兄弟节点w } w.setColor(x.getParent().getColor()); // case4 设兄弟节点w的颜色是x的父节点的颜色 x.getParent().setColor(BLACK); // case4 设x的父节点的颜色为黑色 w.getRight().setColor(BLACK); // case4 设兄弟节点w的右孩子颜色是黑色 leftRotate(root, x.getParent()); // case4 左旋x的父节点 x = root; } // 设x为根节点 } else { // 如果x是其父节点的右孩子 RBTreeNode<Integer> w = x.getParent().getLeft(); // w是x的兄弟节点 if (w.getColor() == RED) { // case1 如果x的兄弟节点是红色的 w.setColor(BLACK); // case1 设兄弟节点w的颜色为黑色 x.getParent().setColor(RED); // case1 设x父节点的颜色为红色 rightRotate(root, x.getParent()); // case1 以x的父节点右旋 w = x.getParent().getLeft(); // case1 重新设置x的兄弟节点w } if (w.getLeft().getColor() == BLACK && w.getRight().getColor() == BLACK) { // case2 如果兄弟节点w的左右孩子颜色都是黑色 w.setColor(RED); // case2 设兄弟节点w的颜色为红色 x = x.getParent(); // case2 设x的父节点为当前节点 } else { if (w.getLeft().getColor() == BLACK) { // case3 如果兄弟节点w的左孩子是黑色 w.getRight().setColor(BLACK); // case3 设兄弟节点w的右孩子是黑色 w.setColor(RED); // case3 设兄弟节点w的颜色是红色 leftRotate(root, w); // case3 左旋兄弟节点w w = x.getParent().getLeft(); // case3 重新设置x的兄弟节点w } w.setColor(x.getParent().getColor()); // case4 设兄弟节点w的颜色是x的父节点的颜色 x.getParent().setColor(BLACK); // case4 设x的父节点的颜色为黑色 w.getLeft().setColor(BLACK); // case4 设兄弟节点w的左孩子颜色是黑色 rightRotate(root, x.getParent()); // case4 右旋x的父节点 x = root; // 设x为根节点 } } x.setColor(BLACK); } } }





