Dijkstra 算法python版

算法策略

Dijkstra 算法是求一个图中一个点到其他所有点的最短路径的算法，先了解图的数据结构「邻接矩阵」

Dijkstra 算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法，时间复杂度 O(n2)

B站视频：https://www.bilibili.com/video/av38254646/?vd_source=3fa2d314205867b74c99b14fd102f85c

要点

每次从 「未求出最短路径的点」中 取出 距离起点 最小路径的点，以这个点为桥梁 刷新「未求出最短路径的点」的距离。

示例

找到以A点为起点，到各个点的最短距离

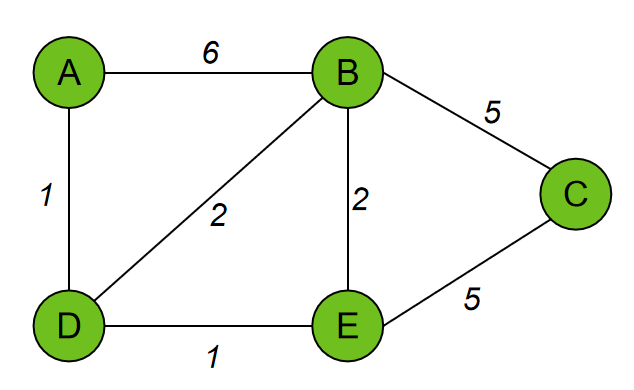
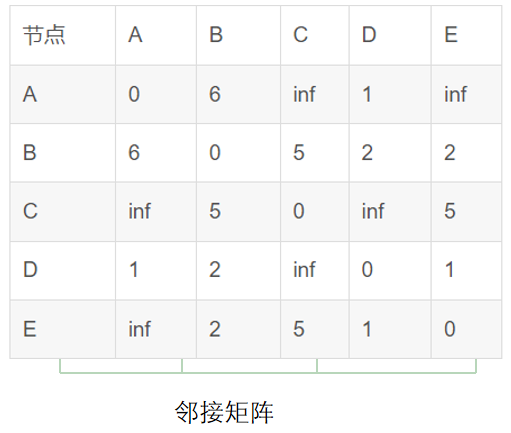
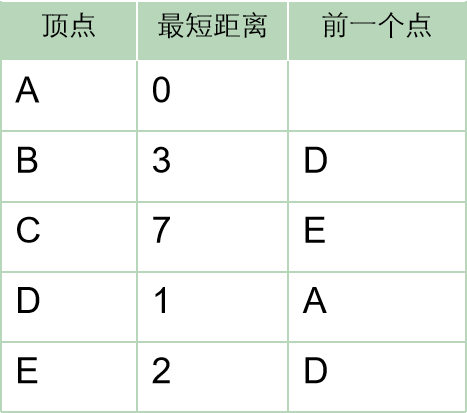
设定初始值

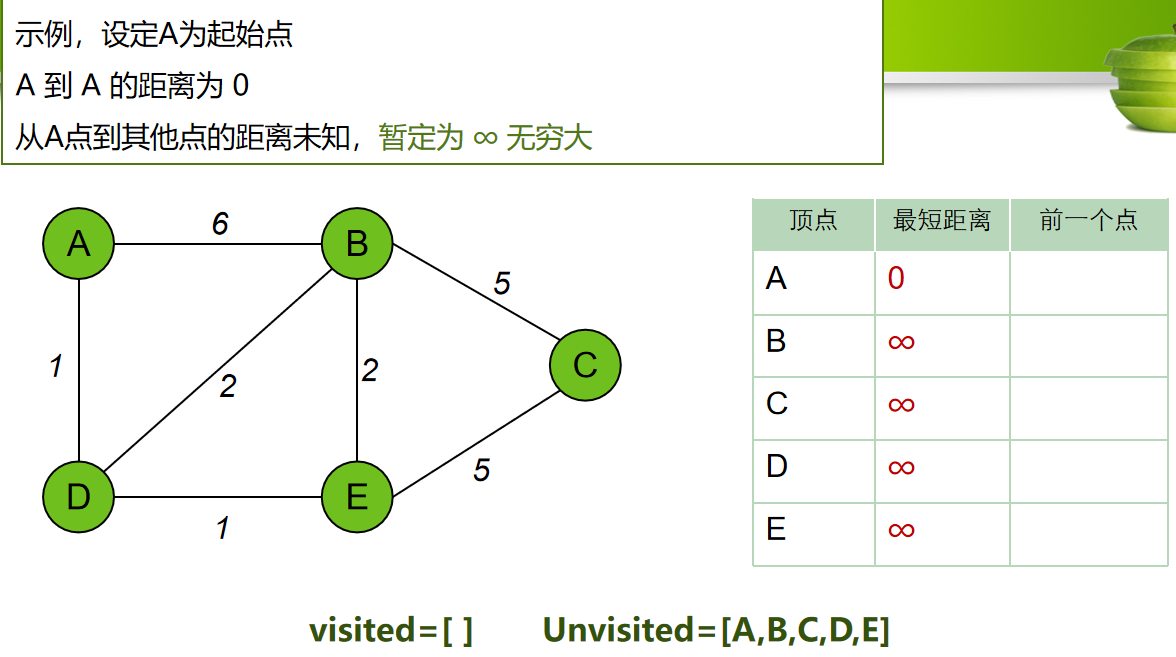
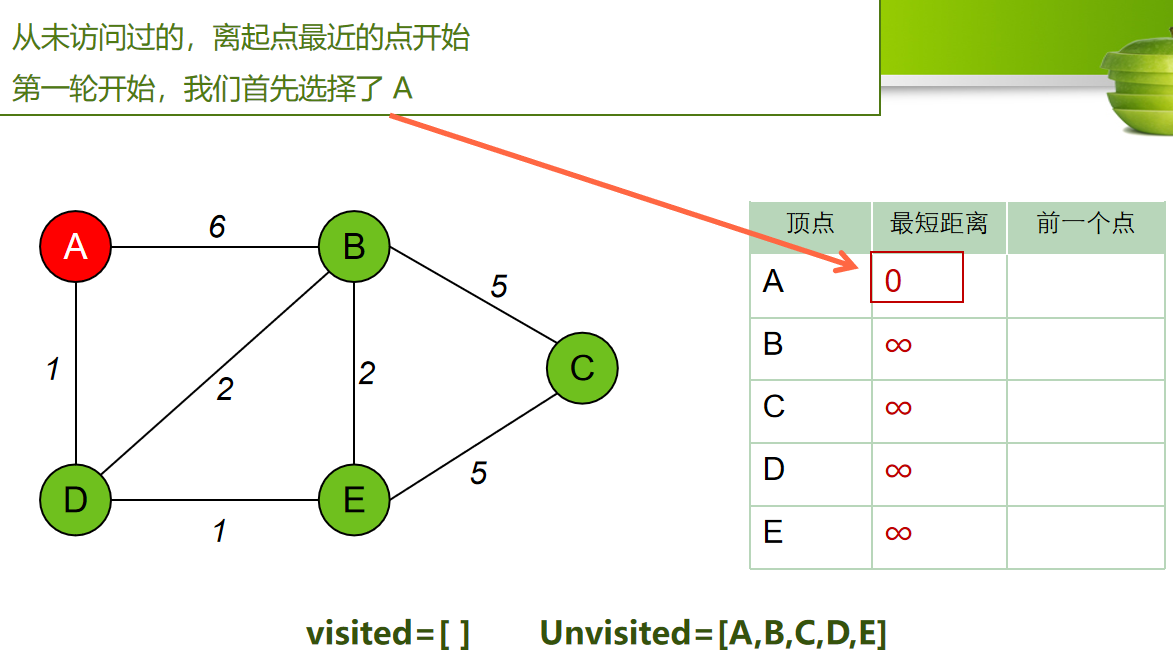
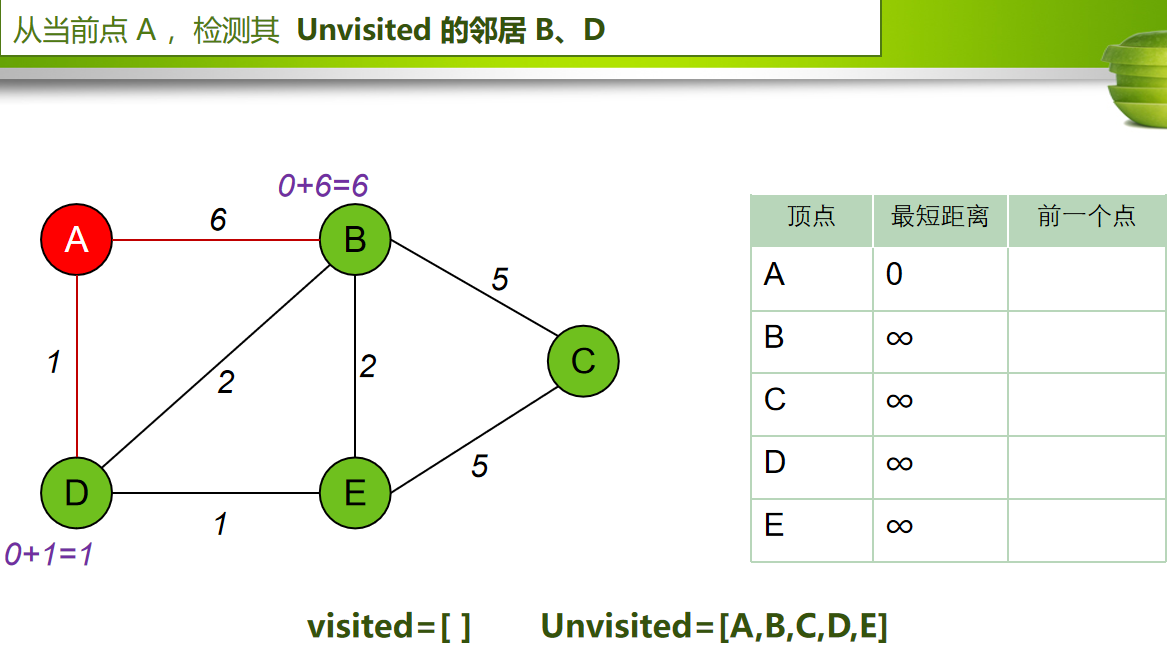
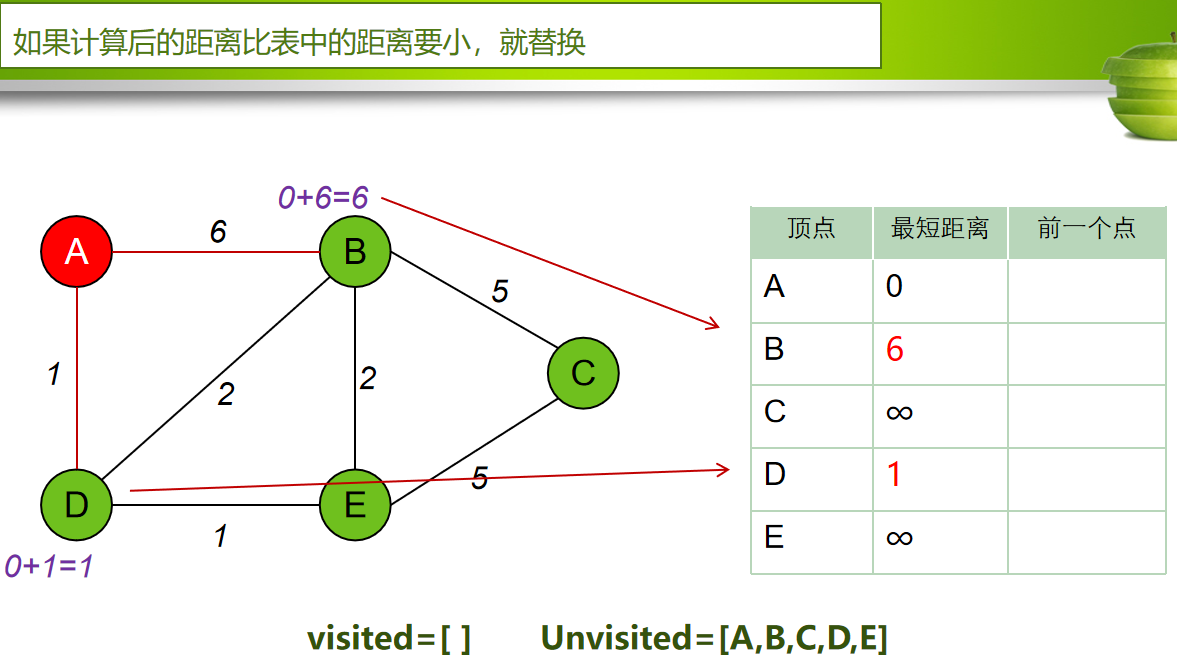
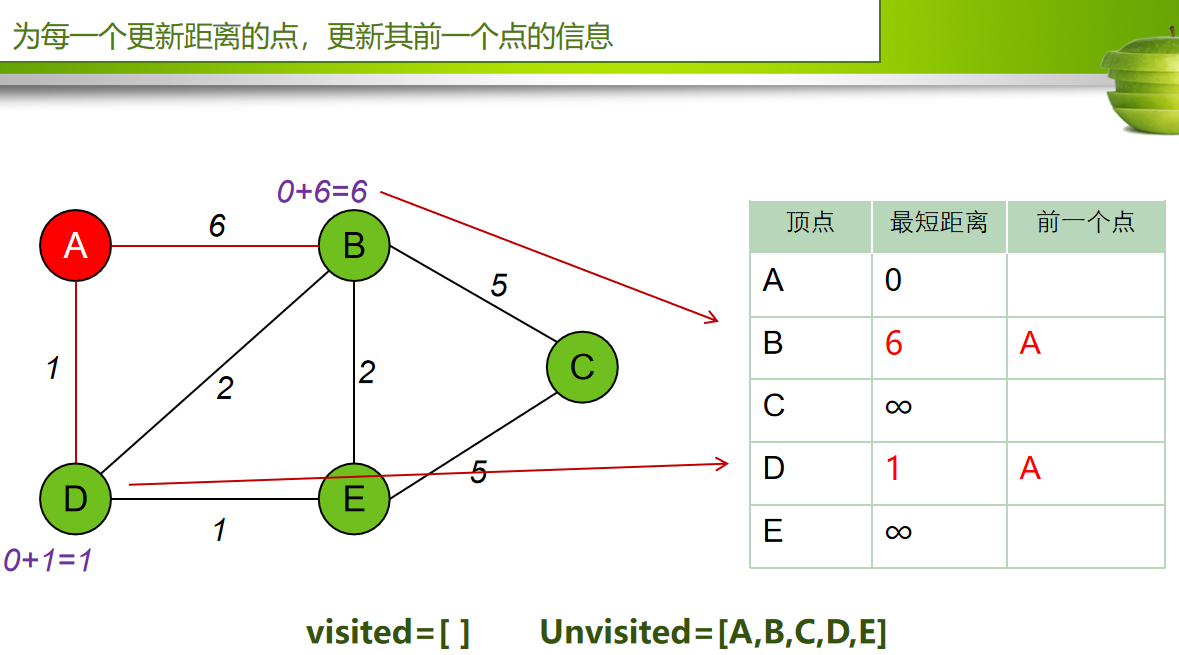
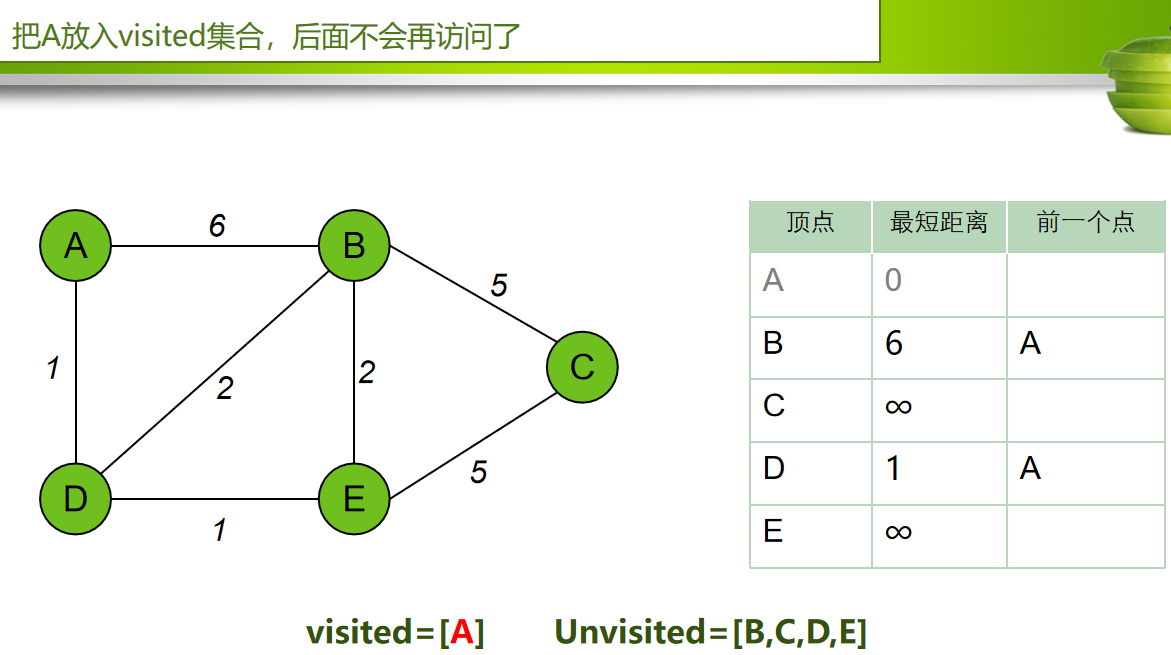
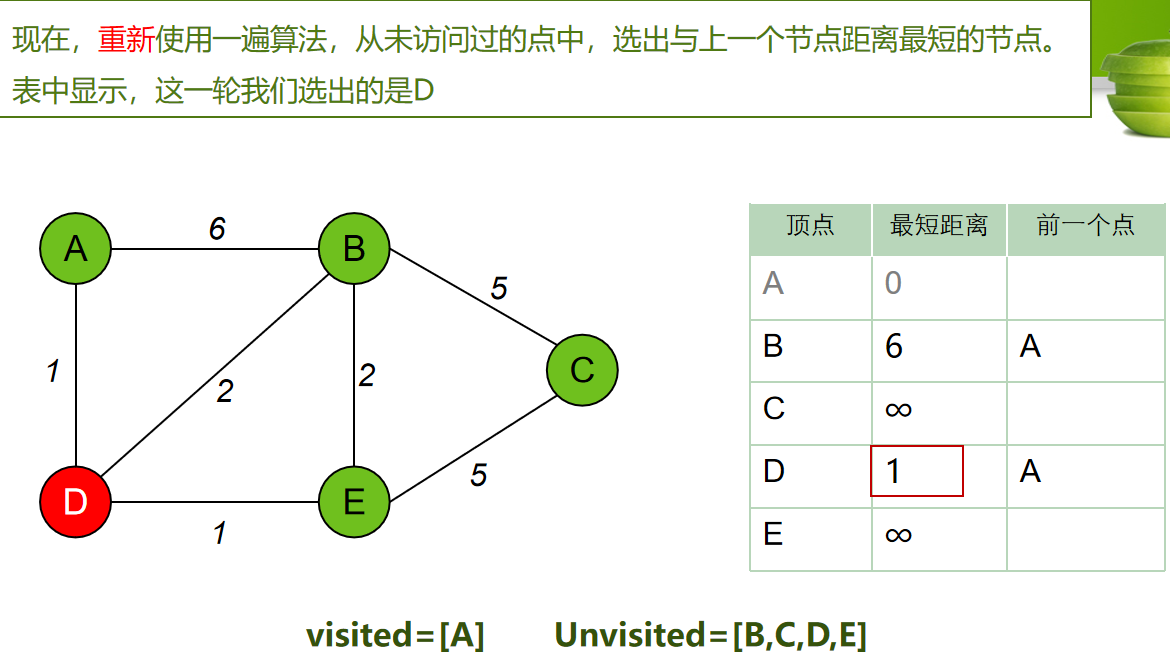
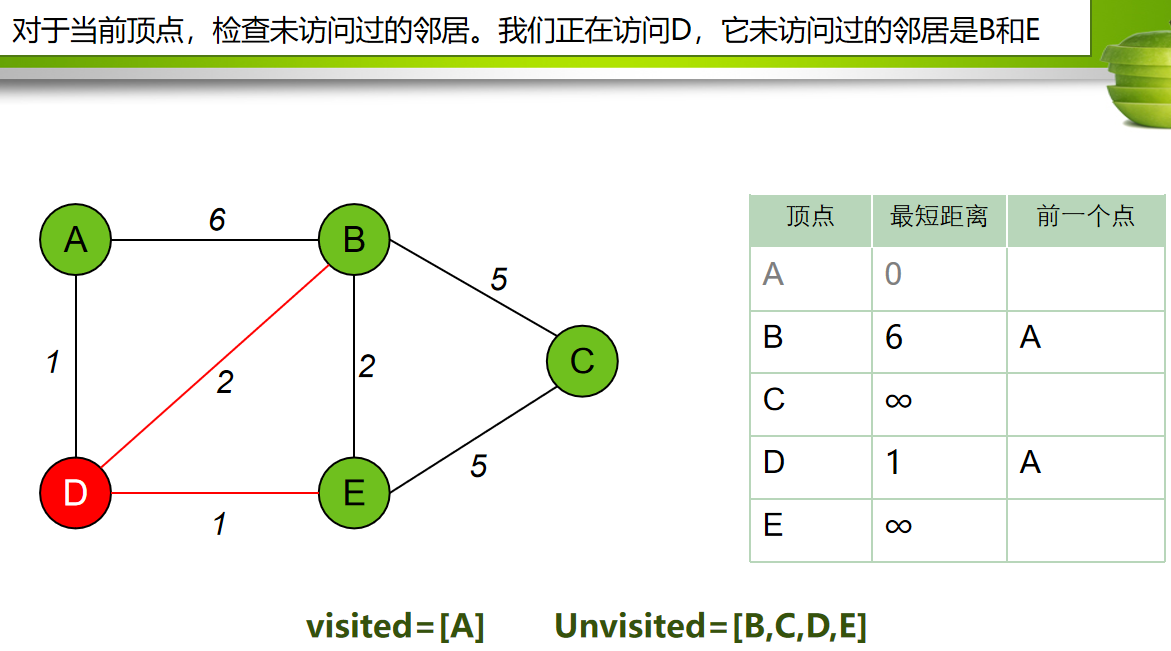
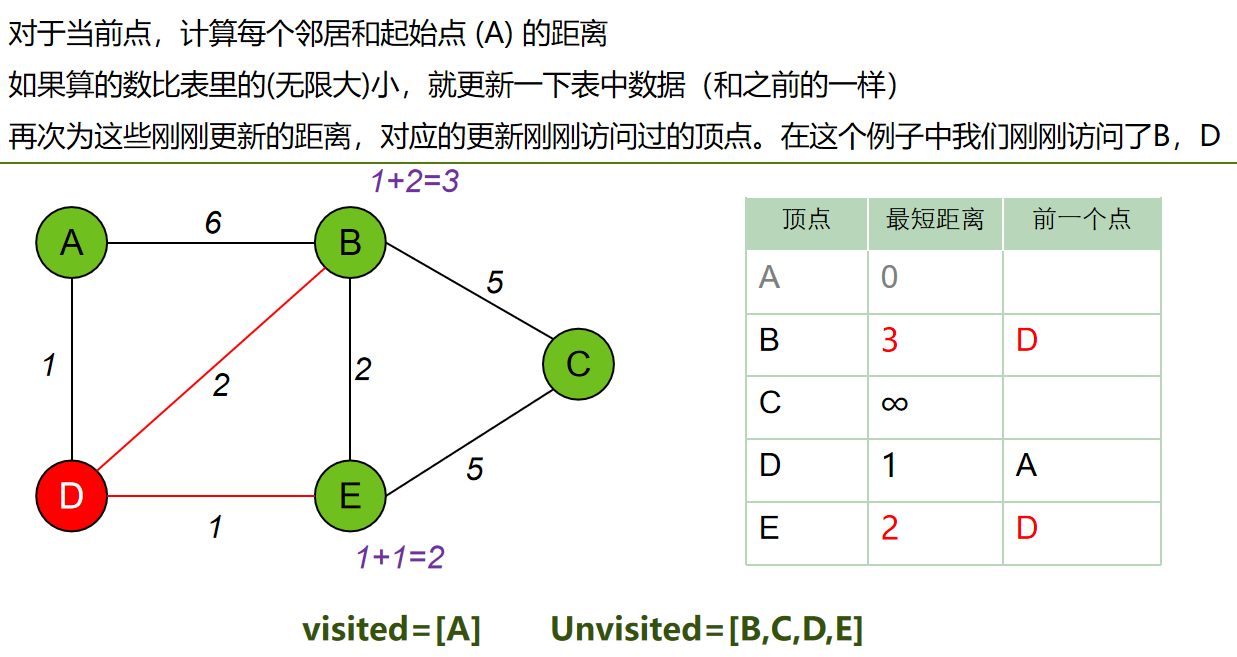
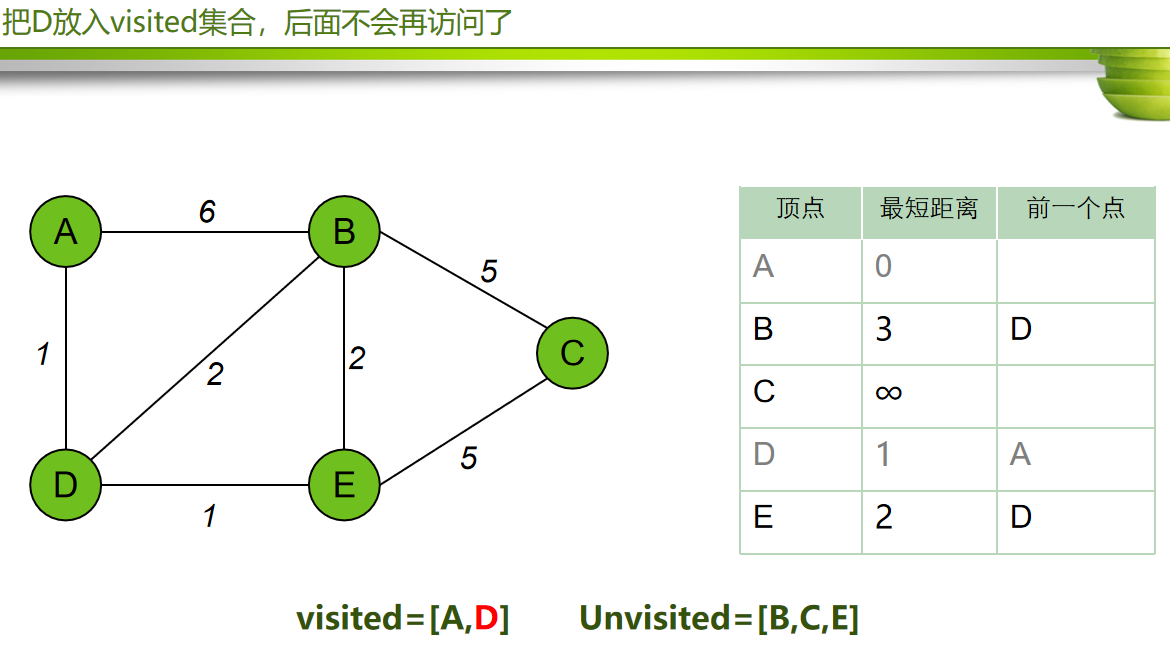
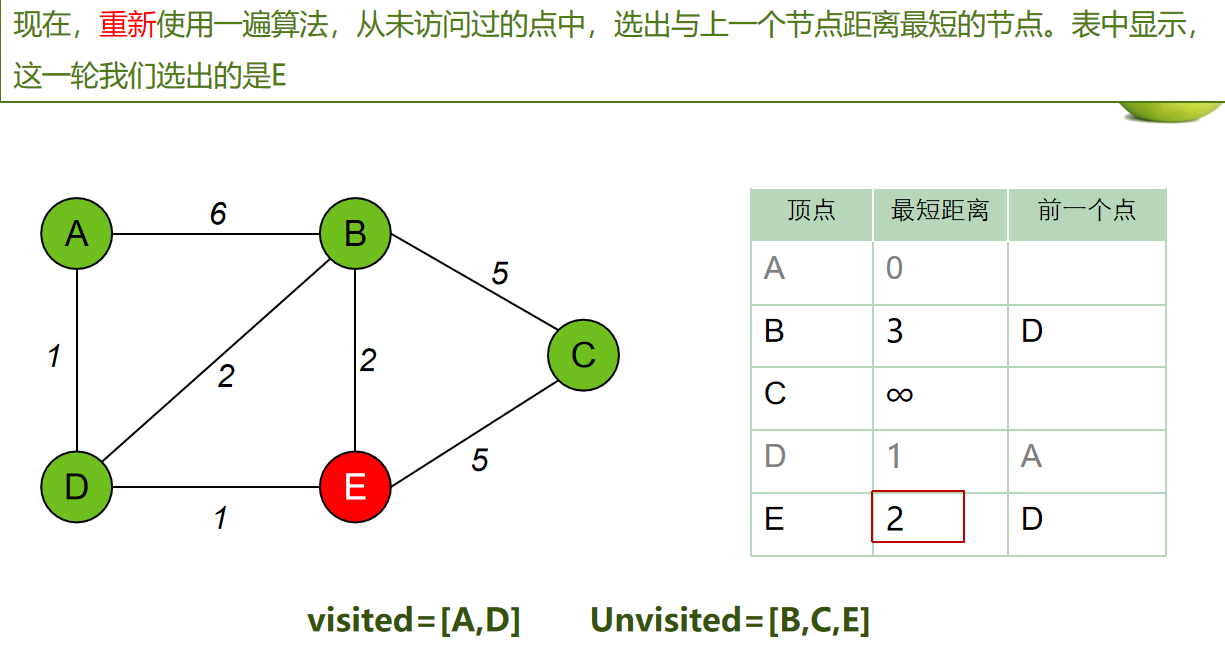
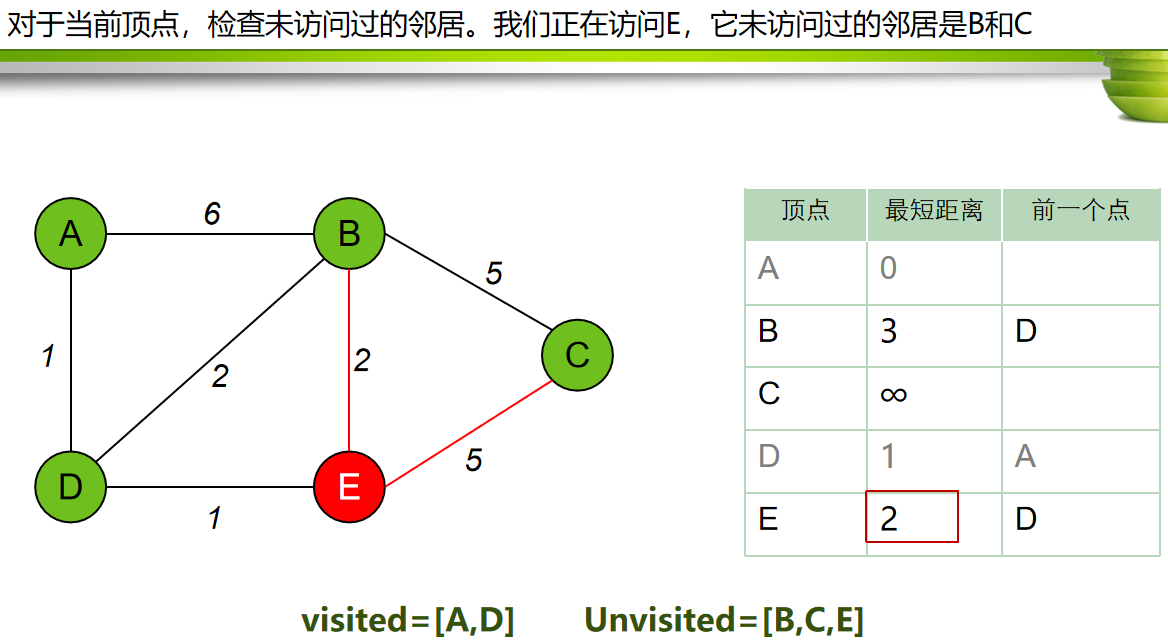
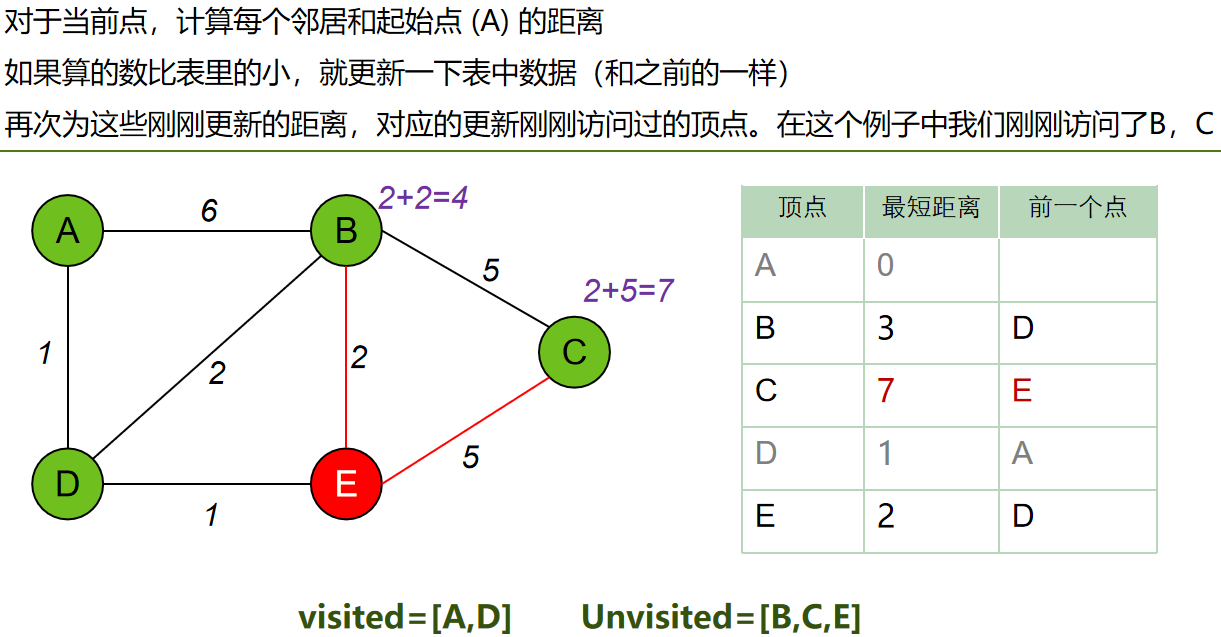
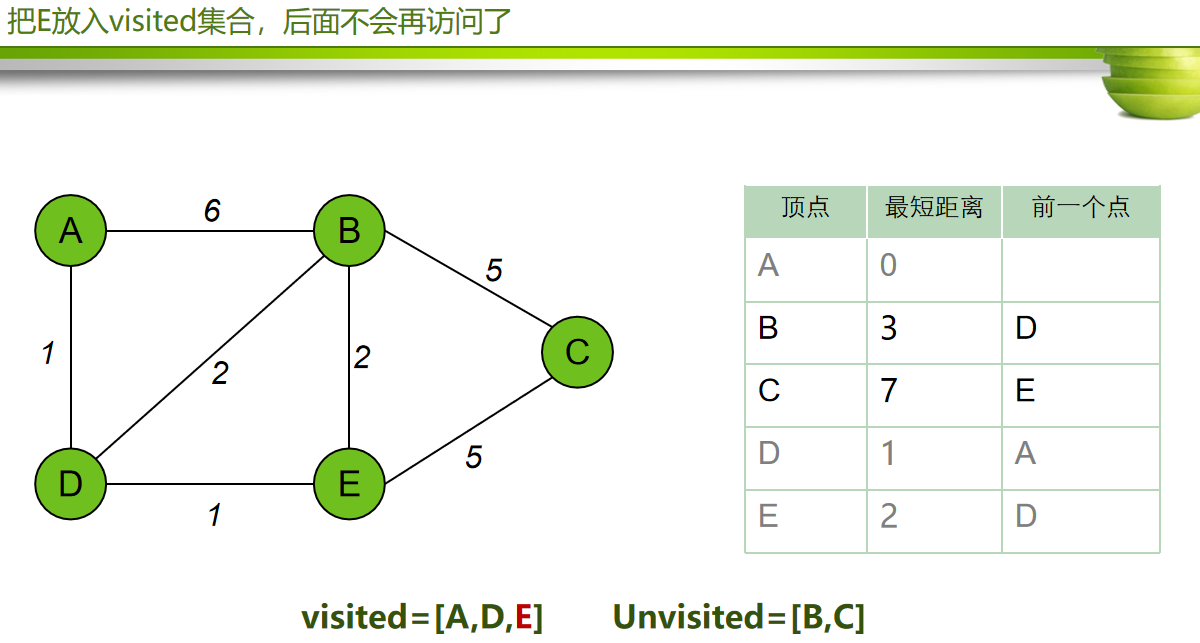
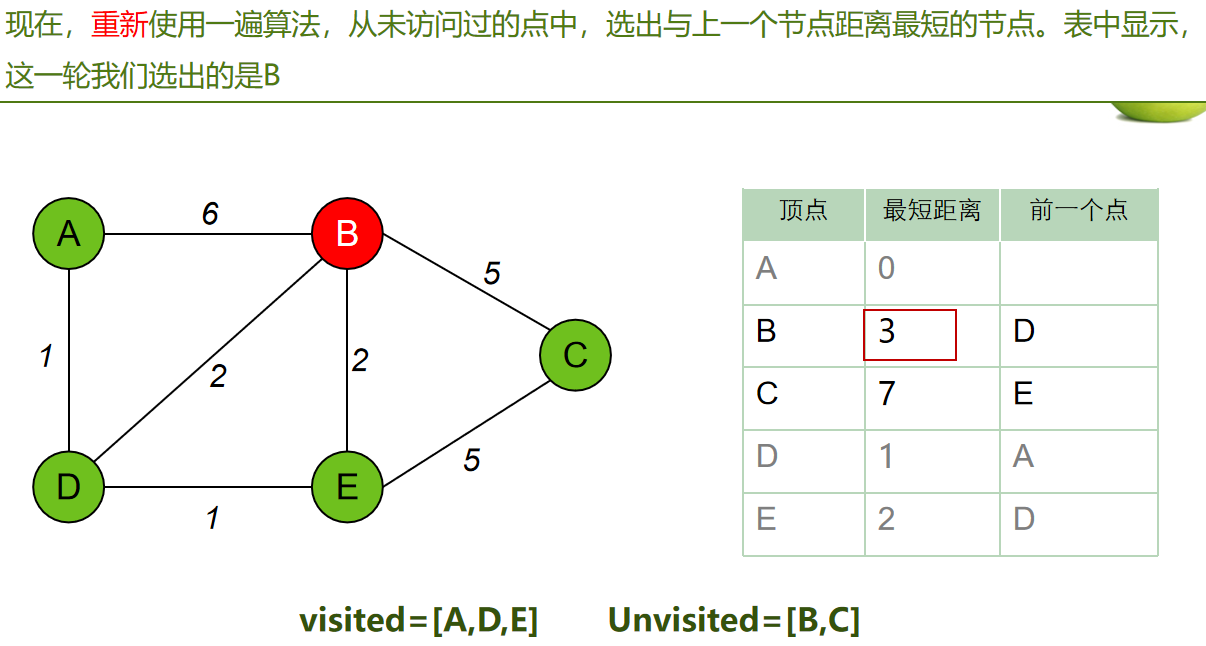
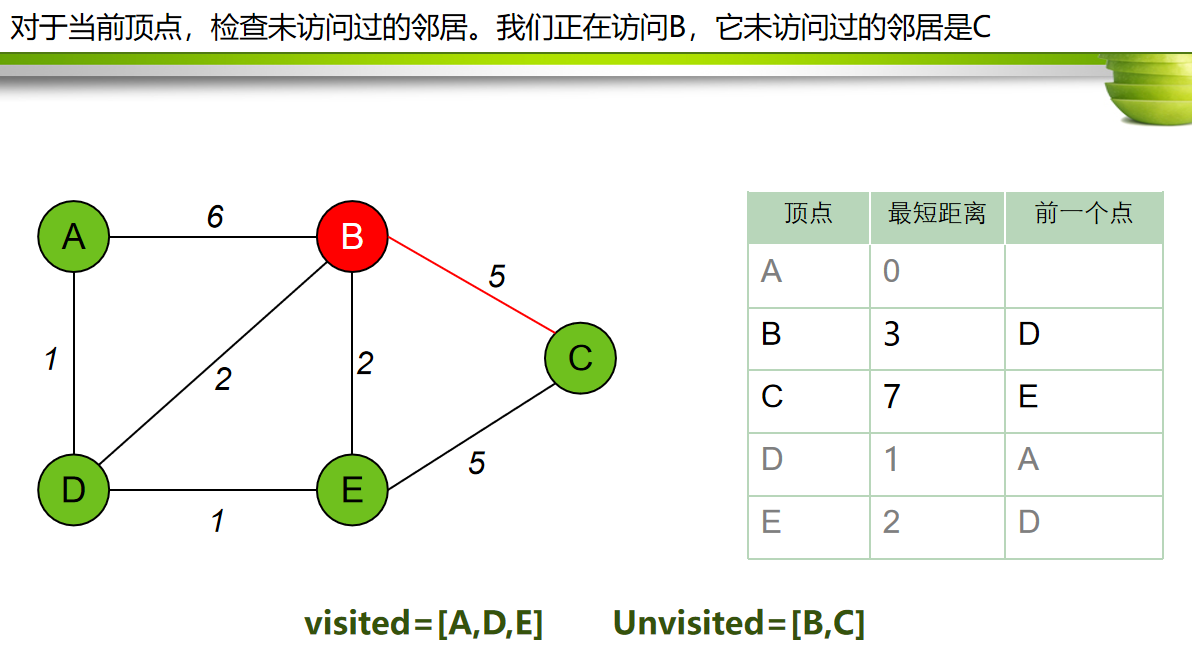
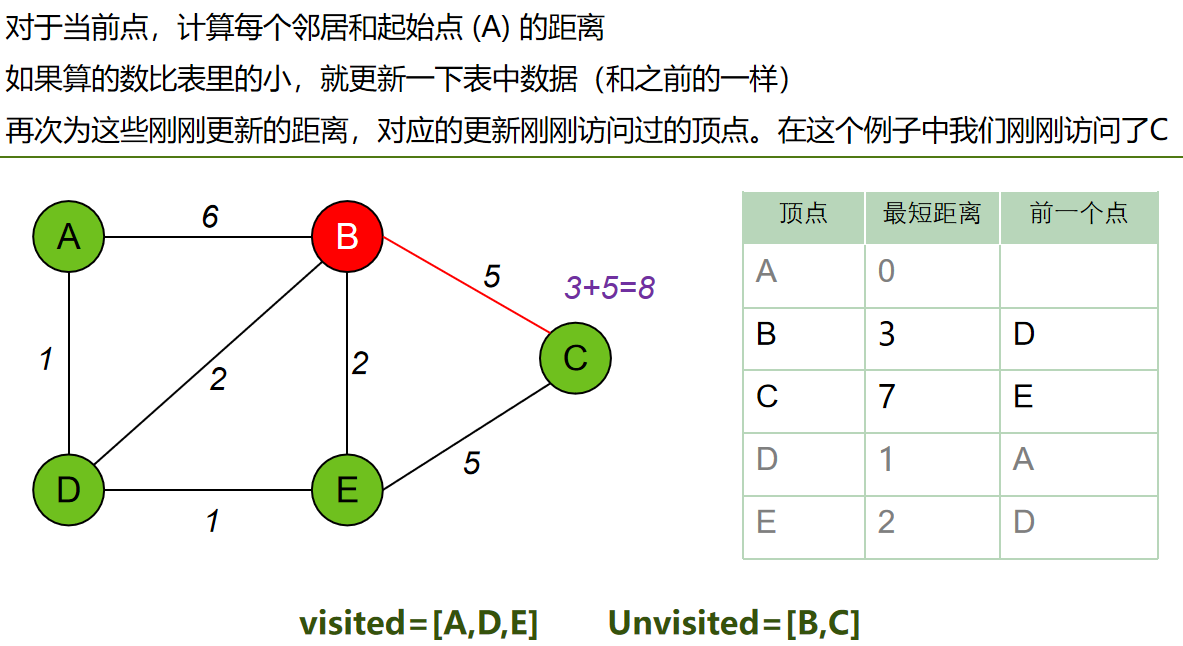
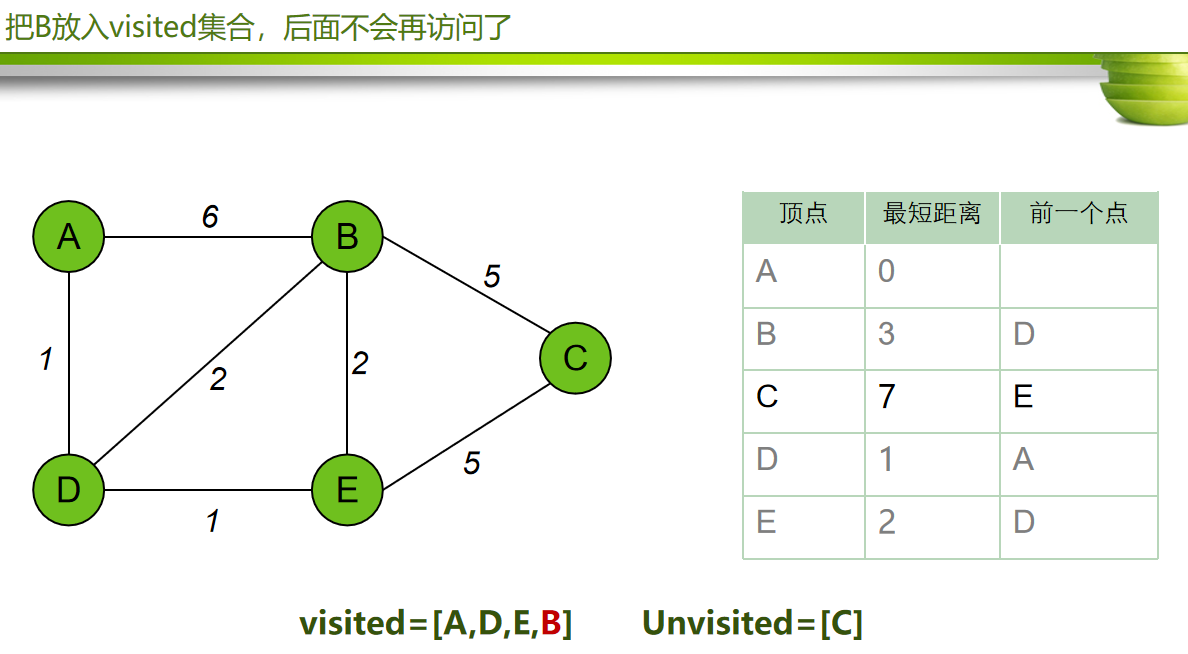
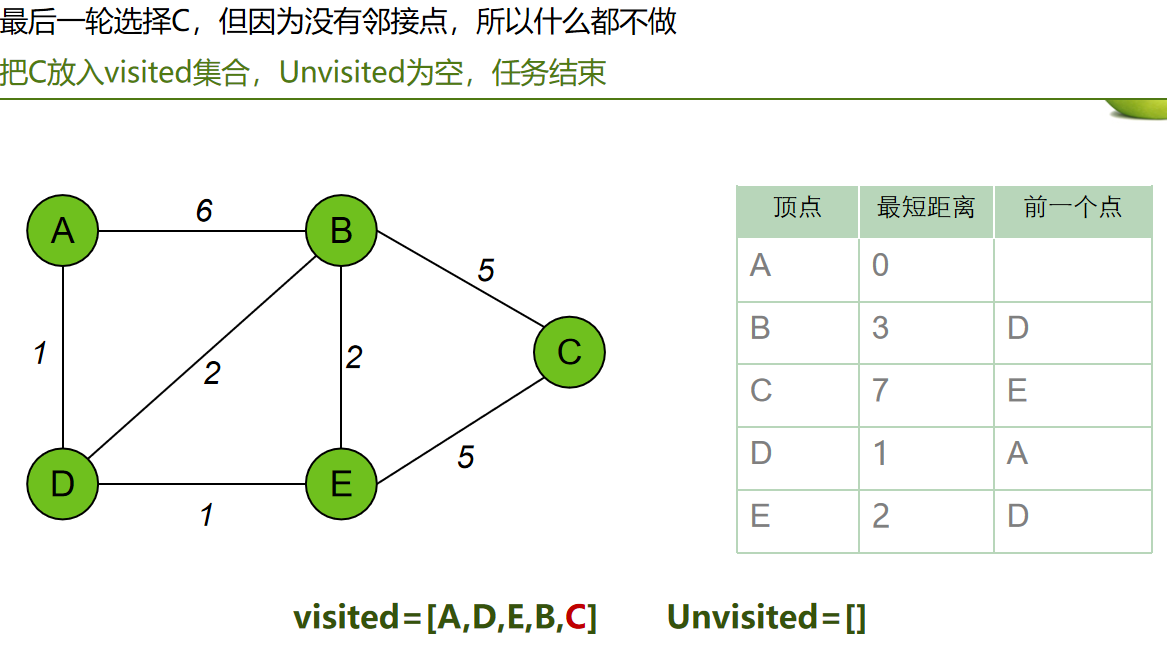
算法步骤

python编码

这是一个完全按照算法步骤进行编写的python代码。没有使用任何库，对算法也没有进行任何优化，但是他是最能反映算法原理的。

def dijkstra(graph, start_index):
    # length = len(graph)
    visited=[]  #[索引，最短距离]
    unvisited=[[x, float('inf')] for x in range(len(graph))] #[索引，最短距离]
    unvisited[start_index][1]=0 # 起始点的初始值设定
 
    #启动dijkstra算法
    while unvisited:  # 遍历未访问节点
        # 查找路径最小值
        min_index = -1  # 设定默认索引为-1
        min_distance = float('inf')  # 设定默认最短路径结点值为无穷大
        for j in range(len(unvisited)):
            if min_distance > unvisited[j][1]:
                min_distance = unvisited[j][1] # 选取最小的路径值的点的值
                min_index = unvisited[j][0]  # 选取最小的路径值的点的索引
        visited.append([min_index,min_distance]) #将最低值点移至visited
        unvisited.remove([min_index,min_distance])
 
        # 更新最短路径数据
        for k in unvisited:  # 找到邻近的结点
            if graph[min_index][k[0]] != -1:  # 有交集（不为-1）
                if min_distance + graph[min_index][k[0]] <k[1]:  # 如果最小的路径值+路径值 比原有的小，即更新
                    k[1] = min_distance + graph[min_index][k[0]]
 
    return [y[1] for y in sorted(visited,key=lambda x:x[0])]
# Test case
# vertices = ['A', 'B', 'C', 'D','E']
graph1 = [
    [0, 6, -1, 1,-1],
    [6, 0, 5, 2, 2],
    [-1, 5, 0, -1,5],
    [1, 2, -1, 0, 1],
    [-1,2, 5, 1, 0]
]
graph2 = [
    [0,10,-1,4,-1,-1],
    [10, 0, 8, 2, 6,-1],
    [-1,8,0,15,1,5],
    [4,2,15,0,6,-1],
    [-1,6,1,6,0,12],
    [-1,-1,5,-1,12,0]
]
graph3 = [
    [0, 2, -1, -1,5],
    [2, 0, 2, -1, -1],
    [-1, 2, 0, 2,-1],
    [-1, -1, 2, 0, 2],
    [5,-1, -1, 2, 0]
]
print(dijkstra(graph3, 0))  # Output: [0, 3, 7, 1, 2]