卷积与Max Pooling(池化)

1、什么是卷积

从数学上讲，卷积就是一种运算。

有这么一副图像，可以看到，图像上有很多噪点：

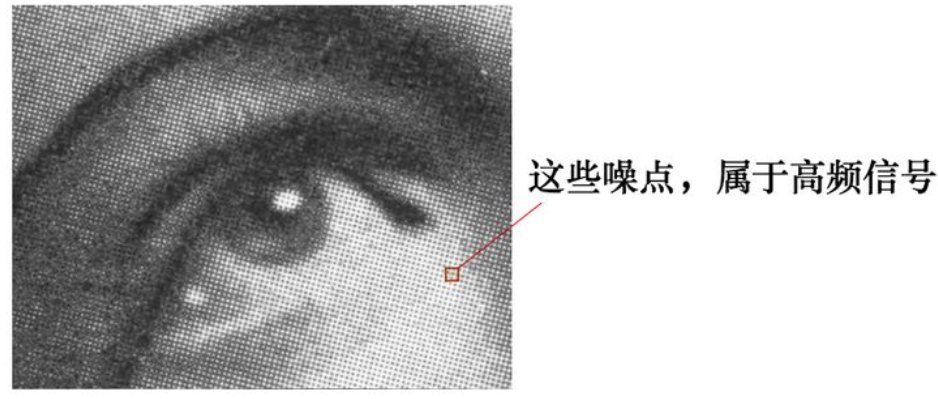
高频信号，就好像平地耸立的山峰：

看起来很显眼。平滑后得到：
平滑这座山峰的办法之一就是，把山峰刨掉一些土，填到山峰周围去。用数学的话来说，就是把山峰周围的高度平均一下。

卷积可以帮助实现这个平滑算法。

有噪点的原图，可以把它转为一个矩阵：

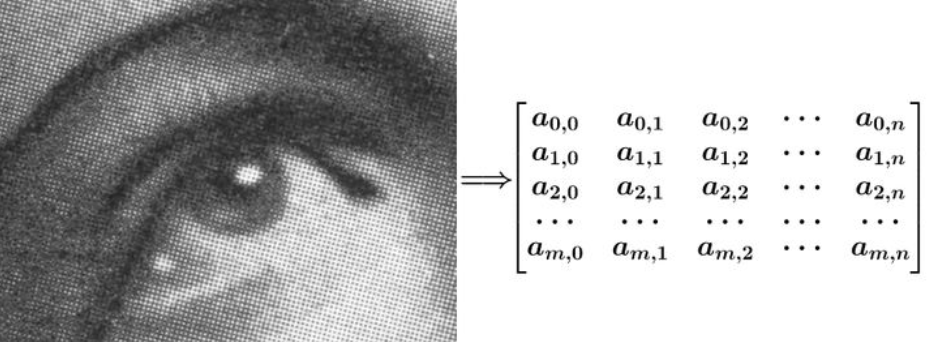
然后用下面这个平均矩阵（说明下，原图的处理实际上用的是正态分布矩阵，这里为了简单，就用了算术平均矩阵）来平滑图像：

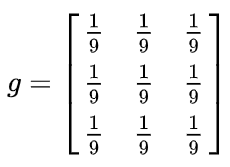
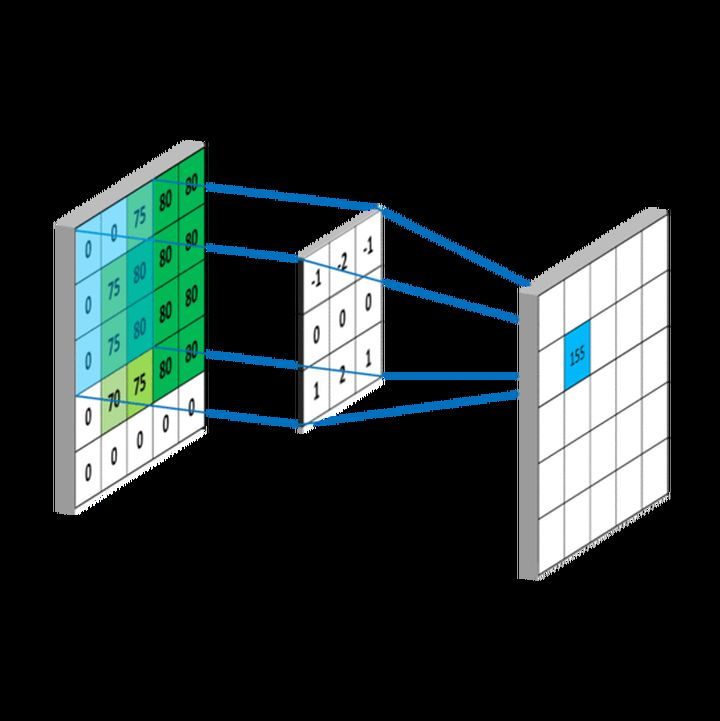
2、什么是Max Pooling(池化)

在卷积后还会有一个 pooling 的操作。

max pooling 的操作如下图所示：整个图片被不重叠的分割成若干个同样大小的小块（pooling size）。每个小块内只取最大的数字，再舍弃其他节点后，保持原有的平面结构得出 output。
注意区分max pooling（最大值池化）和卷积核的操作区别：池化作用于图像中不重合的区域（这与卷积操作不同）

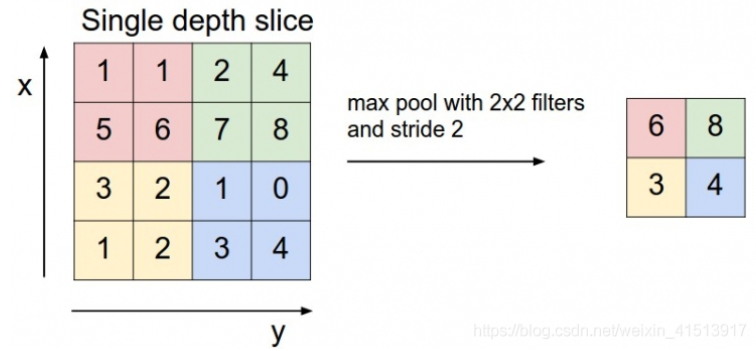
这个图中，原来是4*4的图片。由于不会重合，所以filter的大小和步长stride是相等的，为2.
粉色区域最大值为6，得到的该区域结果是6，绿色是8，黄色是3，紫色是4.

3、Max Pooling的作用

作用1：invariance(不变性)

invariance(不变性)，这种不变性包括translation(平移)不变性，rotation(旋转)不变性，scale(尺度)不变性。

作用2：增大感受野

可能跟作用1的结论有些因果关系。

首先它第一个作用是降低feature map的尺寸，减少需要训练的参数；其次，因为有缩小的作用，所以之前的4个像素点，现在压缩成1个。那么，相当于我透过这1个点，就可以看到前面的4个点，这不就是把当前map的感受野一下子放大了嘛