二叉查找树BST教程
二叉查找树(BST:Binary Search Tree),又称二叉排序树 是一种特殊的二叉树,它改善了二叉树节点查找的效率。二叉查找树有以下性质:
简单概况:小的放左边,大的放右边
对于任意一个节点 n,
其左子树(left subtree)下的每个后代节点(descendant node)的值都小于节点 n 的值;
其右子树(right subtree)下的每个后代节点的值都大于节点 n 的值。
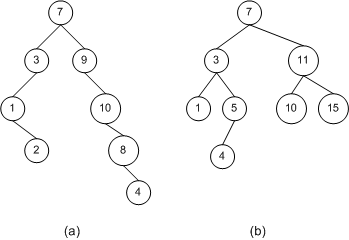
下图中 a 是 错误的,因为 10 的右子树8 比10小,应该放在左子树中。
树的查找
假设我们要查找节点 n,从 BST 的根节点开始。算法不断地比较节点值的大小直到找到该节点,或者判定不存在。每一步我们都要处理两个节点:树中的一个节点,称为节点 c,和要查找的节点 n,然后并比较 c 和 n 的值。开始时,节点 c 为 BST 的根节点。然后执行以下步骤:
如果 c 值为空,则 n 不在 BST 中;
比较 c 和 n 的值;
如果值相同,则找到了指定节点 n;
如果 n 的值小于 c,那么如果 n 存在,必然在 c 的左子树中。回到第 1 步,将 c 的左孩子作为 c;
如果 n 的值大于 c,那么如果 n 存在,必然在 c 的右子树中。回到第 1 步,将 c 的右孩子作为 c;
查找算法的时间复杂度应该是 O(log2n),简写为 O(lg n)
而实际上,对于 BST 查找算法来说,其十分依赖于树中节点的拓扑结构,也就是节点间的布局关系。下图描绘了一个节点插入顺序为 20, 50, 90, 150, 175, 200 的 BST 树。这些节点是按照递升顺序被插入的,结果就是这棵树没有广度(Breadth)可言。也就是说,它的拓扑结构其实就是将节点排布在一条线上,而不是以扇形结构散开,所以查找时间也为 O(n)。
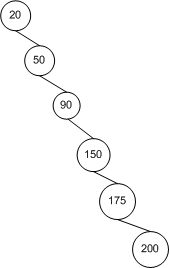
BST 算法查找时间依赖于树的拓扑结构。最佳情况是 O(log2n),而最坏情况是 O(n)
树的插入
BST 的插入算法的复杂度与查找算法的复杂度是一样的:最佳情况是 O(log2n),而最坏情况是 O(n)。因为它们对节点的查找定位策略是相同的。
节点的删除
从 BST 中删除节点比插入节点难度更大。因为删除一个非叶子节点,就必须选择其他节点来填补因删除节点所造成的树的断裂。如果不选择节点来填补这个断裂,那么就违背了 BST 的性质要求。
删除节点算法的第一步是定位要被删除的节点,这可以使用前面介绍的查找算法,因此运行时间为 O(log2n)。接着应该选择合适的节点来代替删除节点的位置,它共有三种情况需要考虑。
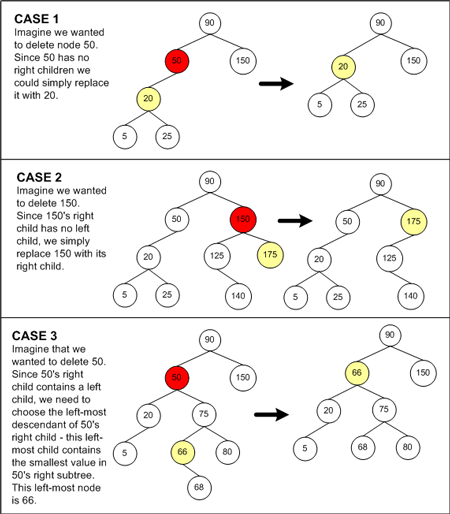
- 情况 1:如果删除的节点没有右孩子,那么就选择它的左孩子来代替原来的节点。二叉查找树的性质保证了被删除节点的左子树必然符合二叉查找树的性质。因此左子树的值要么都大于,要么都小于被删除节点的父节点的值,这取决于被删除节点是左孩子还是右孩子。因此用被删除节点的左子树来替代被删除节点,是完全符合二叉搜索树的性质的。
- 情况 2:如果被删除节点的右孩子没有左孩子,那么这个右孩子被用来替换被删除节点。因为被删除节点的右孩子都大于被删除节点左子树的所有节点,同时也大于或小于被删除节点的父节点,这同样取决于被删除节点是左孩子还是右孩子。因此,用右孩子来替换被删除节点,符合二叉查找树的性质。
- 情况 3:如果被删除节点的右孩子有左孩子,就需要用被删除节点右孩子的左子树中的最下面的节点来替换它,就是说,我们用被删除节点的右子树中最小值的节点来替换。
删除算法的运行时间也与 BST 的拓扑结构有关,最佳情况是 O(log2n),而最坏情况是 O(n)
遍历节点
前序遍历(Perorder traversal)
中序遍历(Inorder traversal)
后序遍历(Postorder traversal)
参考>https://www.cnblogs.com/gaochundong/p/binary_search_tree.html





