白话深度神经网络

为什么要整出个深度神经网络？

先从方程说起

1、一元线性方程

首先说 一元线性方程

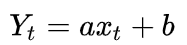
已知 x， y，通过算法探求 x->y 的规律，也就是计算 a，b的 值。 常用的算法 最小二乘法

2、多元线性方程

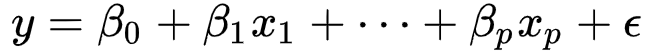
已知 x， y，通过算法探求 x->y 的规律，也就是计算 各个β，ε的 值。 常用的算法 最小二乘法

看到这里，大家发现了吗 多元方程 比 一元方程参数更多了。多元方程实际意义更大，因为现实世界影响结果的因素更加多。

3、还可不可以更复杂一些呢？

多项式方程！

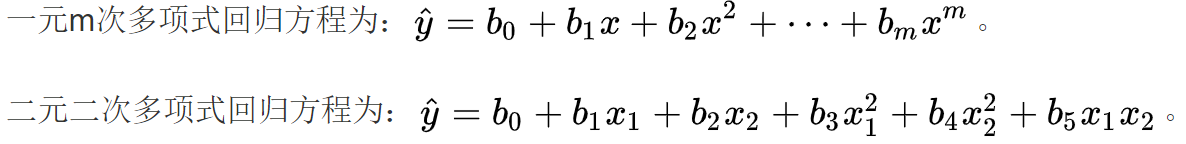
大家注意到，计算的复杂度又增加了，参数又增多了。

4、还可不可以再复杂一些呢？

重点：

以上图的 二元方程为例。如果参数 β1 本身 是由一个 线性方程！ 线性方程！ 线性方程！ （重要的事情说三遍！） 构成的，是不是可以更加 精确描述一个模型！

如果 β1 是由一个线性方程构成的，那么 像什么？像什么？像什么？ 矩阵！矩阵！矩阵！ 就是把 参数由一行的变成多行！

这样就可以先初步理解什么是神经网络了。

就是搞很多参数（矩阵参数），通过估算矩阵的 w ，来进行回归(非线性)！

---

进阶

理解了上面的，我们开始进一步思考。
因为已知的x，y均有多个值。而且，这里面的规律，不能仅仅是简单的线性回归，那么 引入 非线性回归！ 非线性回归！ 非线性回归！

为什么非要引入非线性回归？

例如例如神经网络进行分辨 猫的照片，你能用简单的线性归回，或是多元线性回归，总结出猫的模样吗？当然不可能！

再例如，预测房价，似乎是有规律，但是细想一下，房价的构成因素多种多样，关键是，各种各样的因素，在不同的购买者内心的 权重 是不一样的！这才是最关键的！ 例如 ，我最关心的是学区房，他最关心的地铁房，她最关心的是周边环境。因此无法一言以蔽之，就是无法用多元线性回归来完成标准化。

因此，线性的解决不了， 那就 非线性吧。

---

激活层

首先不要被名字吓到，单纯从名字来看是无法理解的。你可理解为 增强！ 过滤！。
他们的计算都很简单
激活层是为矩阵运算的结果添加非线性的过滤、增强。
常用的激活函数有三种，分别是阶跃函数、Sigmoid和ReLU。如下图（更正：sigmoid在负无穷是应趋近于0）：

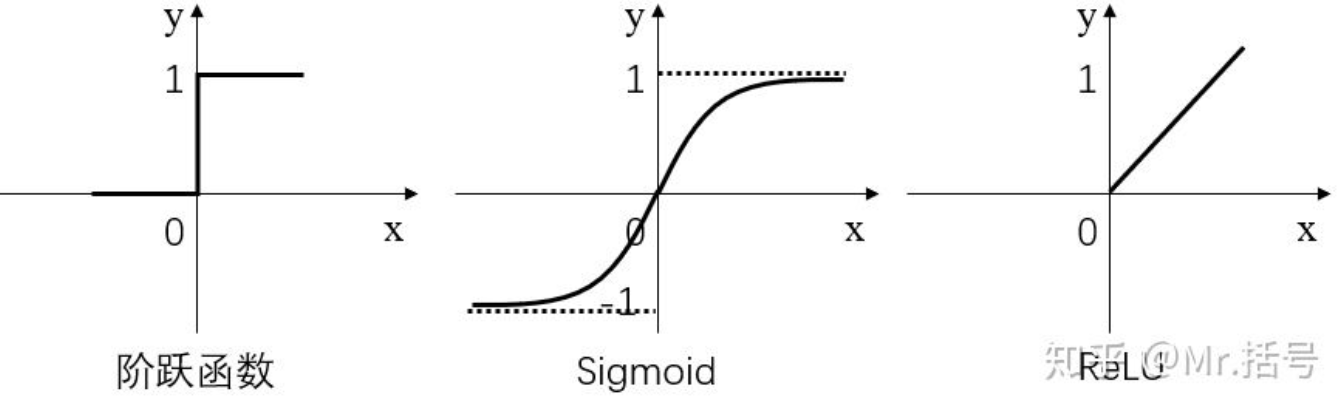
• 阶跃函数：当输入小于等于0时，输出0；当输入大于0时，输出1。
• Sigmoid：当输入趋近于正无穷/负无穷时，输出无限接近于1/0。
• ReLU：当输入小于0时，输出0；当输入大于0时，输出等于输入。

其中，阶跃函数输出值是跳变的，且只有二值，较少使用；Sigmoid函数在当x的绝对值较大时，曲线的斜率变化很小（梯度消失），并且计算较复杂；ReLU是当前较为常用的激活函数。

激活函数具体是怎么计算的呢？

假如经过公式计算得到的结果值为：(1,-2,3,-4,7...)，
那么如果经过 阶跃函数激活层 后就会变为(1,0,1,0,1...)
如果经过 ReLU激活层 之后会变为(1,0,3,0,7...)。

隐藏层

顾名思义，隐藏的层。为什么叫隐藏？因为 你也搞不懂里面在捣鼓什么。就像我们 吃的饭，拉出来的屎。中间的消化过程，其实是非常非常复杂的，现代医学也就是 通过 消化系统 来称呼它。如果有了问题，只能头痛医头脚痛医脚。如果医生也搞不定了，就会告诉你一些名词：
脾胃不和！不和！不和！
内分泌紊乱! 紊乱! 紊乱!
免疫系统抵抗力 低下！低下！低下！巴拉巴拉

既然说不清，就让它再 玄妙 些吧，就叫 隐藏层！

典型的神经网络应用，如识别猫的照片，根本无法清楚的知道我们该怎么设定参数？设定多少参数？
这就是为什么我们只能大概估计一下设 50层，或者60层，总之，层数越多，相当于描述 内部的运算逻辑（过滤系统） 越复杂，就越精确贴近目标。
但是问题又来了，太精确了，就会出现问题，过拟合。

过拟合

参数越多，越贴近已知的目标，对于未知的测试数据，可能是个灾难。
例如，学习画小猫，当你画了1000种猫了，现在让你画老虎，你的结构比例，可能还是一只猫。因为，在你的意识里，大猫也得是这个比例。这个意识哪来的？就是通过你不断的学习得来的或者说在你大脑中的“隐藏层”积累下来的。
当然 你可能说，我学的是画猫，为什么让我画老虎？当然画不好了。我这是举个极端的例子，当你的模型过分 拟合于 现有的数据，对于新的测试数据，可能就是个灾难。

再比如，你把马云、马化腾的成长过程建立一套模型，你按照那个模型发展，你就未必能成功！ 所以模型太精准于描述当前数据，对测试数据集未必能够更好的描述。
这就叫 过拟合。拟合（贴近）的过分了！过分了！过分了！过分了！

---

神经网络讲得最简单直观的两篇文章，感谢 简书的墨功科技、知乎的Mr.括号。
本文很多部分内容摘自上述两篇文章。再次感谢！
两篇文章一定要一起看，两位大佬角度不太一样！

知乎大佬Mr.括号

神经网络15分钟入门！足够通俗易懂了吧

结合自己的理解再转发一下，做好笔记！

任务描述

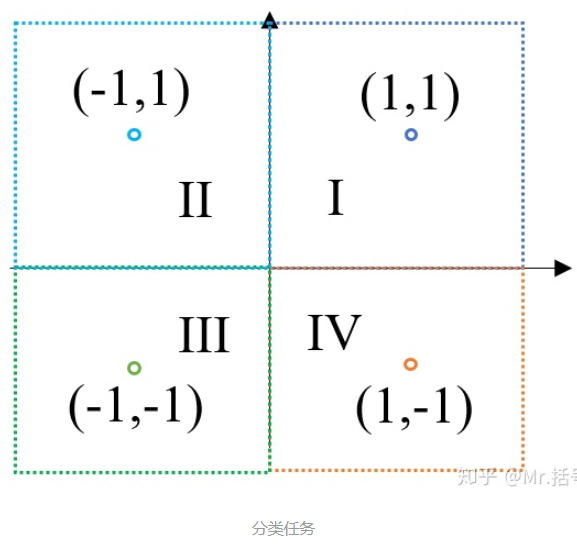
如下图，我们已知四个数据点(1,1)(-1,1)(-1,-1)(1,-1)，这四个点分别对应I~IV象限，如果这时候给我们一个新的坐标点（比如(2,2)），那么它应该属于哪个象限呢？（没错，当然是第I象限，但我们的任务是要让机器知道）

“分类”是神经网络的一大应用，我们使用神经网络完成这个分类任务。

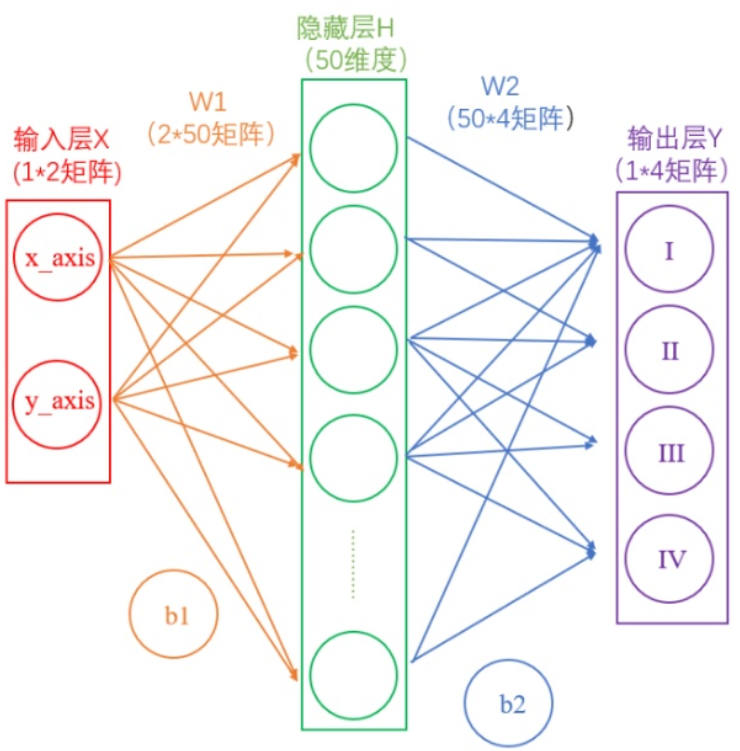
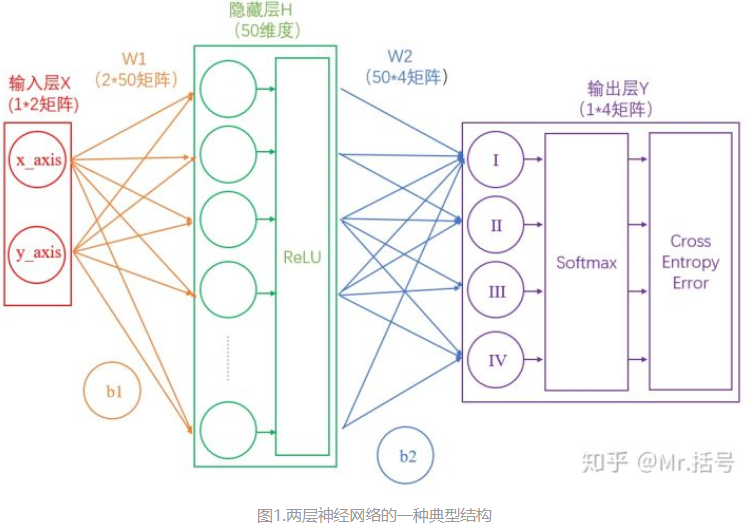
两层神经网络

这里我们构建一个两层神经网络，理论上两层神经网络已经可以拟合任意函数。这个神经网络的结构如下图：

1.简化的两层神经网络分析

首先去掉图1中一些难懂的东西，如下图（请仔细看一下图中的标注）：

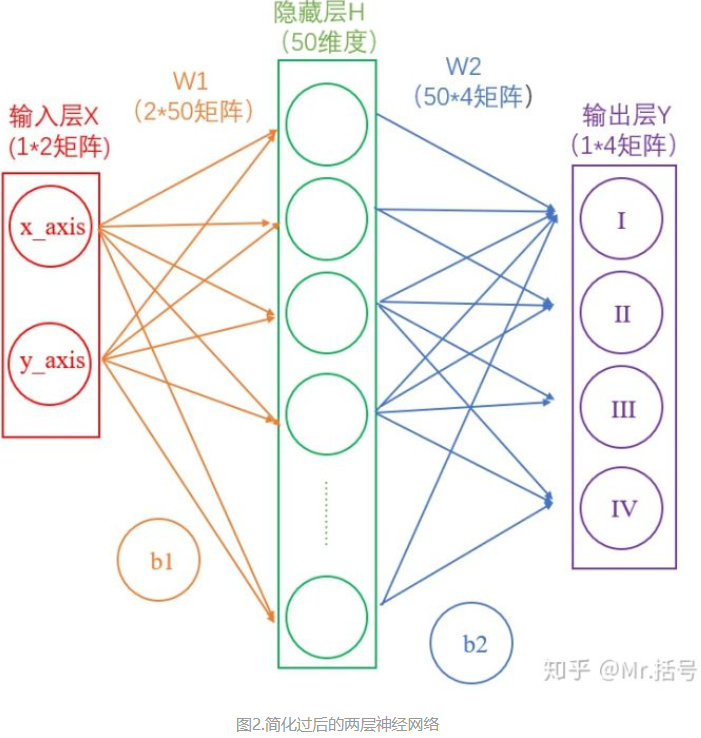
1.1.输入层

在我们的例子中，输入层是坐标值，例如（1,1），这是一个包含两个元素的数组，也可以看作是一个12的矩阵。输入层的元素维度与输入量的特征息息相关，如果输入的是一张3232像素的灰度图像，那么输入层的维度就是32*32。

1.2.从输入层到隐藏层

连接输入层和隐藏层的是W1和b1。由X计算得到H十分简单，就是矩阵运算：

如上图中所示，在设定隐藏层为50维（也可以理解成50个神经元）之后，矩阵H的大小为（1*50）的矩阵。

1.3.从隐藏层到输出层

连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的：

1.4.分析

通过上述两个线性方程的计算，我们就能得到最终的输出Y了，但是如果你还对线性代数的计算有印象的话，应该会知道：一系列线性方程的运算最终都可以用一个线性方程表示。也就是说，上述两个式子联立后还是一个线性方程。对于两次神经网络是这样，就算网络深度加到100层，也依然是线性的。这样的话神经网络就失去了意义。

所以这里要对网络注入灵魂：激活层。

2.激活层

简而言之，激活层是为矩阵运算的结果添加非线性的。常用的激活函数有三种，分别是阶跃函数、Sigmoid和ReLU。不要被奇怪的函数名吓到，其实它们的形式都很简单，如下图（更正：sigmoid在负无穷是应趋近于0）：

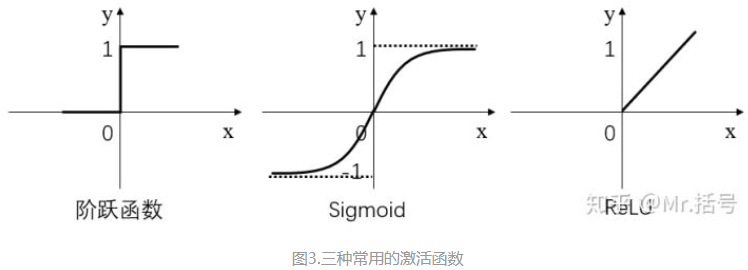
• 阶跃函数：当输入小于等于0时，输出0；当输入大于0时，输出1。
• Sigmoid：当输入趋近于正无穷/负无穷时，输出无限接近于1/0。
• ReLU：当输入小于0时，输出0；当输入大于0时，输出等于输入。

其中，阶跃函数输出值是跳变的，且只有二值，较少使用；Sigmoid函数在当x的绝对值较大时，曲线的斜率变化很小（梯度消失），并且计算较复杂；ReLU是当前较为常用的激活函数。

激活函数具体是怎么计算的呢？

假如经过公式H=X*W1+b1计算得到的H值为：(1,-2,3,-4,7...)，那么经过阶跃函数激活层后就会变为(1,0,1,0,1...)，经过ReLU激活层之后会变为(1,0,3,0,7...)。

需要注意的是，每个隐藏层计算（矩阵线性运算）之后，都需要加一层激活层，要不然该层线性计算是没有意义的。

此时的神经网络变成了如下图所示的形式：

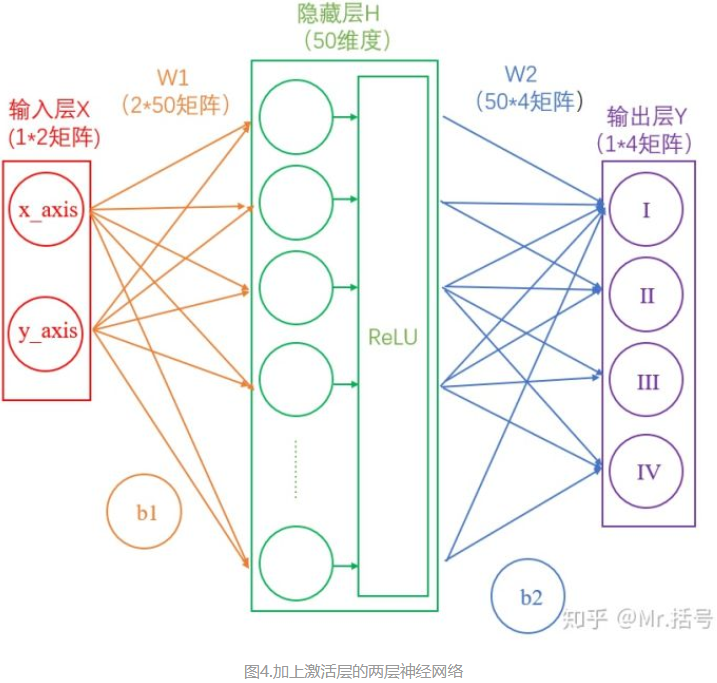
神经网络是分为“训练”和“使用”两个步骤的。如果是在“使用”的步骤，图4就已经完成整个过程了，在求得的Y（大小为1*4）矩阵中，数值最大的就代表着当前分类。

但是对于用于“训练”的网络，图4还远远不够。起码当前的输出Y，还不够“漂亮”。

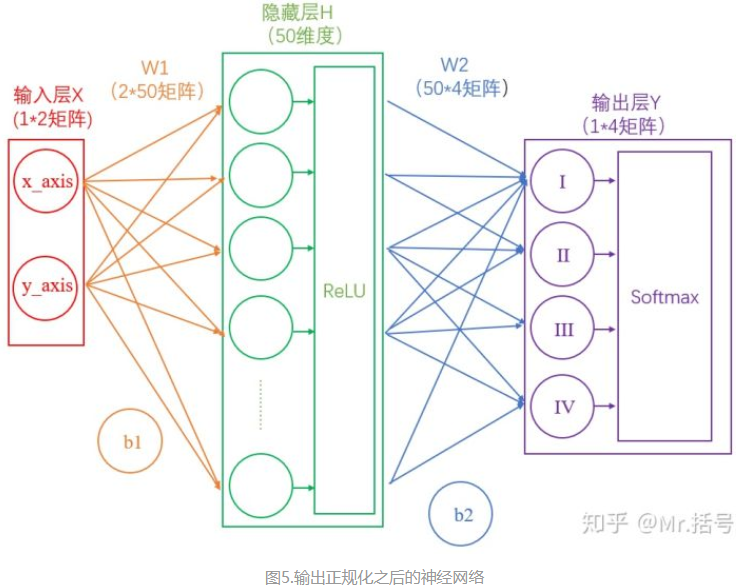
3.输出的正规化

在图4中，输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵，诚然我们可以找到里边的最大值“3”，从而找到对应的分类为I，但是这并不直观。我们想让最终的输出为概率，也就是说可以生成像(90%,5%,2%,3%)这样的结果，这样做不仅可以找到最大概率的分类，而且可以知道各个分类计算的概率值。

具体是怎么计算的呢？

计算公式如下：

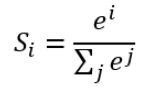
简单来说分三步进行：（1）以e为底对所有元素求指数幂；（2）将所有指数幂求和；（3）分别将这些指数幂与该和做商。

这样求出的结果中，所有元素的和一定为1，而每个元素可以代表概率值。

我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成如下图所示：

4.如何衡量输出的好坏

通过Softmax层之后，我们得到了I，II，III和IV这四个类别分别对应的概率，但是要注意，这是神经网络计算得到的概率值结果，而非真实的情况。

比如，Softmax输出的结果是(90%,5%,3%,2%)，真实的结果是(100%,0,0,0)。虽然输出的结果可以正确分类，但是与真实结果之间是有差距的，一个优秀的网络对结果的预测要无限接近于100%，为此，我们需要将Softmax输出结果的好坏程度做一个“量化”。

一种直观的解决方法，是用1减去Softmax输出的概率，比如1-90%=0.1。不过更为常用且巧妙的方法是，求对数的负数。

还是用90%举例，对数的负数就是：-log0.9=0.046

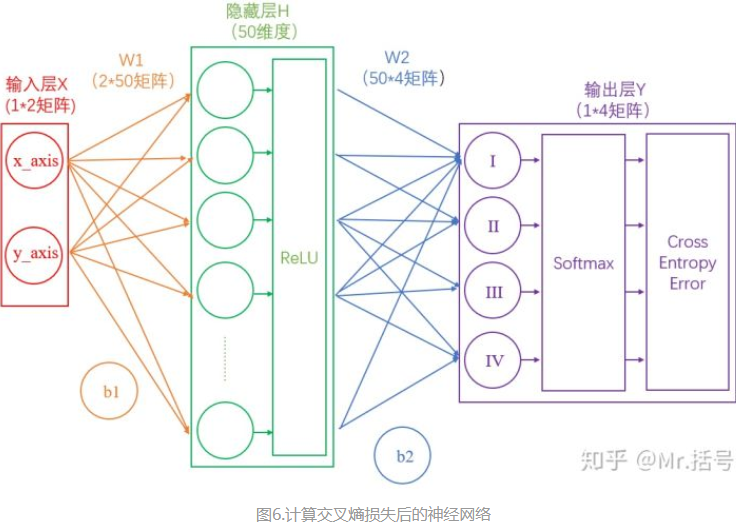
可以想见，概率越接近100%，该计算结果值越接近于0，说明结果越准确，该输出叫做“交叉熵损失（Cross Entropy Error）”。

我们训练神经网络的目的，就是尽可能地减少这个“交叉熵损失”。

此时的网络如下图：

5.反向传播与参数优化

上边的1~4节，讲述了神经网络的正向传播过程。一句话复习一下：神经网络的传播都是形如Y=WX+b的矩阵运算；为了给矩阵运算加入非线性，需要在隐藏层中加入激活层；输出层结果需要经过Softmax层处理为概率值，并通过交叉熵损失来量化当前网络的优劣。

算出交叉熵损失后，就要开始反向传播了。其实反向传播就是一个参数优化的过程，优化对象就是网络中的所有W和b（因为其他所有参数都是确定的）。

神经网络的神奇之处，就在于它可以自动做W和b的优化，在深度学习中，参数的数量有时会上亿，不过其优化的原理和我们这个两层神经网络是一样的。

这里举一个形象的例子描述一下这个参数优化的原理和过程：

假设我们操纵着一个球型机器行走在沙漠中

我们在机器中操纵着四个旋钮，分别叫做W1，b1，W2，b2。当我们旋转其中的某个旋钮时，球形机器会发生移动，但是旋转旋钮大小和机器运动方向之间的对应关系是不知道的。而我们的目的就是走到沙漠的最低点。

此时我们该怎么办？只能挨个试喽。

如果增大W1后，球向上走了，那就减小W1。

如果增大b1后，球向下走了，那就继续增大b1。

如果增大W2后，球向下走了一大截，那就多增大些W2。

。。。

这就是进行参数优化的形象解释（有没有想到求导？），这个方法叫做梯度下降法。

当我们的球形机器走到最低点时，也就代表着我们的交叉熵损失达到最小（接近于0）。

关于反向传播，还有许多可以讲的，但是因为内容较多，就放在下一篇文章中说吧。不过上述例子对于理解神经网络参数优化的过程，还是很有帮助的。

6.迭代

神经网络需要反复迭代。

如上述例子中，第一次计算得到的概率是90%，交叉熵损失值是0.046；将该损失值反向传播，使W1,b1,W2,b2做相应微调；再做第二次运算，此时的概率可能就会提高到92%，相应地，损失值也会下降，然后再反向传播损失值，微调参数W1,b1,W2,b2。依次类推，损失值越来越小，直到我们满意为止。

此时我们就得到了理想的W1,b1,W2,b2。

此时如果将任意一组坐标作为输入，利用图4或图5的流程，就能得到分类结果。

---

简书大佬墨攻科技

30分钟讲清楚深度神经网络

转发一遍，做个笔记！

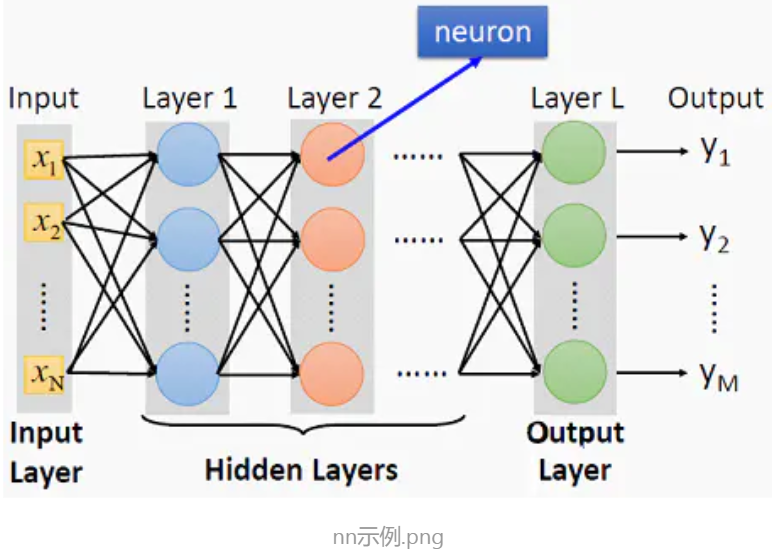
神经网络是啥

建立M个隐藏层，按顺序建立输入层跟隐藏层的联结，最后建立隐藏层跟输出层的联结。为每个隐藏层的每个节点选择激活函数。求解每个联结的权重和每个节点自带的bias值。参见下图。

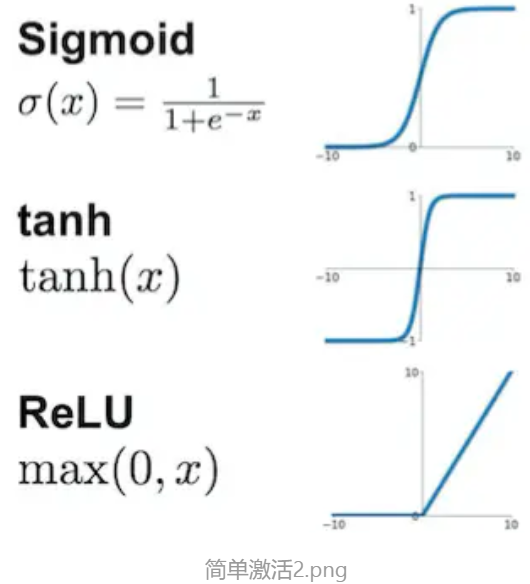
所谓激活函数就是对各个路径的输入求和之后，进一步增强的函数 。
典型的有如下几个：

神经网络训练的本质

一题道出本质
下面这个图里面，是已知的各个联结线的权值，求y1, y2

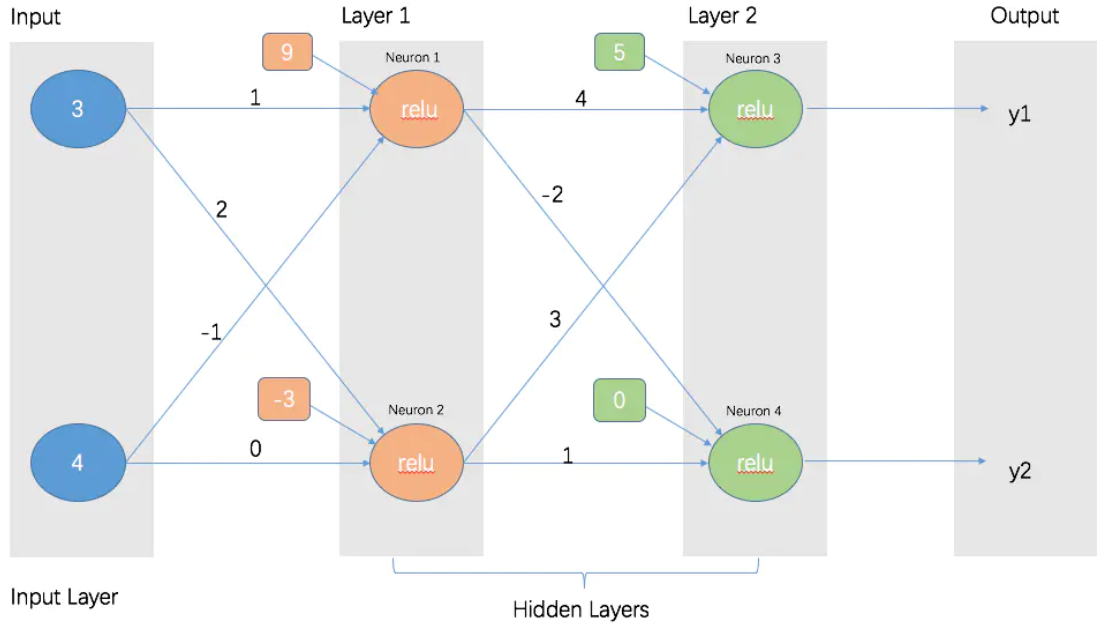
这个练习可以测试对神经网络的理解。

答案是 y1 = 46, y2 = 0

其实就是 权值 乘以 输入值 加上 偏差值之后，再通过激活函数对结果进行一次处理，得出的输出就是该节点最终的结果。

所以，Layer 1中的Neuron1的值为 n1 = max(3 * 1 + 4 * (-1) + 9, 0) = 8。
Neuron2的值为 n2 = max(3 * 2 + 4 * 0 + (-3), 0) = 3。
Layer 2中的Neuron3 值为 n3 = max(n1 * 4 + n2 * 3 + 5, 0) = 46。
Neuron4的值为 n4 = max(n1 * (-2) + n2 * 1 + 0, 0) = 0。 （注意 取最大值）

所谓神经网络问题的训练本质，就是已知 y1,y2....yn， 已知x1, x2....xm，求解每个连接的权值和每个神经元上的偏差值。对单层的激活函数为RELU的神经网络而言就是， y = max(sum(w * x)+b, 0)，已知y和x，求解w和b。

训练的方法

对于以上求解w和b的值，科学家们发现可以通过反向传播和梯度下降相结合来求解。就是一开始用随机数初始化我们每个联结的权值，然后通过神经网络计算出来的y值跟真实的y值做比对。如果这个值相差比较大，则修改当前层的联结的权重。当发现这个值相差不大时，则修改更低一层的权重。这个步骤一直重复，逐步传递到第一层的权值。

神经网络求解遇到的问题

三大问题：

神经网络的原生问题：

• 求解时会遇到梯度消失或者梯度爆炸
• 性能，训练太慢
• 过拟合
  针对这三个问题，大拿们开始了一场探索之旅。

梯度消失或爆炸的解决方案

神经网络的求解是通过反向传播的技术来解决的。通过梯度下降法。问题是，反向传播从输出层开始一步一步传到Layer1时，越到低层，联结的权值变化越小，直到没变化。这种叫梯度消失。还有一些呢？则是越到第一层，变化越来越大。这种叫梯度爆炸。常见于RNN。

解决方案探索如下：
解决方案探索如下：

• 1.联结权重的初始化放弃完全随机的方式，而是要使用特定的标准差。有He initialization和Xavier initialization
• 2.使用ReLU作为激活函数。后面发现ReLU里面某些神经元会变成0（Dying ReLU的问题)，这个时候又演化出 LReLU，RReLU和PReLU以及ELU这些变种。一般来说，激活函数的选择优先顺序有 ELU > leaky ReLu（包括LReLU,RReLU,PReLU） > ReLU > tanh > sigmoid
• 3.Batch Normalization。就是在每层都对输入的X进行转化，变成以0为中心的分布。最终求解同时要求出每层用来scale的参数应该是多少。
• 4.Gradient Clipping。就是在反向传播的过程中限制梯度不超过某个阈值。如果超过就减去相应的阈值。
  目前来说，通常用1+2 多于 3 多于 4。就是现在一般使用He initialization跟ReLU的演进版本作为激活函数来解决梯度消失和爆炸的问题，其次才使用Batch Normalization，最后使用Gradient Clipping。

性能问题的解决方案

通常来说，我们很难获得足够的标记好的训练数据。常用解决方案如下：

• 1. 复用已有的训练好的网络。通常可以找到已经训练好的模型的地方有 tensorflow的github caffe的github
• 2. unsupervised pretraining。对无标签的训练数据，直接运行类似于autoencoders之类的算法。这种算法类似于聚类，可以提取出输入数据里面较为核心的特征出来。通过这样一步一步生成每一个隐藏层。最后再用有标签的数据来训练最终的网络。

对于大规模数据的训练，很多时候速度很慢。除了解决梯度消失或爆炸的问题之外，还有使用AdamOptimizer替代GradientDescentOptimizer会大大加快收敛速度。

过拟合的解决方案

• 1.early stopping。一旦发现在验证集合上性能下降，立即停止训练
• 2.在cost function上添加L1 L2 Regularization。所谓L1 L2的Regularization就是添加对模型复杂度的惩罚项。模型用到的联结线权值越大，惩罚越大。这样模型的优化目标就不仅仅是要预测偏差尽量小，同时还要预测所使用的模型尽量简单。
• 3.使用Dropout。就是每次随机选择一些神经元不参与训练，只有在预测的时候这些神经元才生效。这个神经元的输出结果要乘以一个概率值。降低贡献。其实这种就有点类似于降低了神经元之间的依赖性。原来是每个联结的神经元都参与计算的。现在是随机失效了。这种技术竟然可以稳定的为神经网络的能力提升2%！
• 4.max-norm regularization。就是限制每个神经元的联结的weight的 l2 Regularization在一个阈值内。
• 5.数据补充。其实就是对已有的训练数据做一定的变换，用来做训练。提升模型泛化能力

一个神经网络的默认最优配置

Initialization	Activation function	Normalization	Regularization	Optimizer
He Initialization	ELU	Batch Normalization	Dropout	AdamOptimizer