动态规划LeetCode377 求方案数

给定一个由正整数组成且不存在重复数字的数组 nums，找出和为给定目标正整数 target 的组合的个数。顺序不同的序列视作不同的组合。
示例：nums = [1, 2, 3]，target = 4。所有可能的组合为：

(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

动态规划

dp[i]，i= 1 ~ target

转移方程

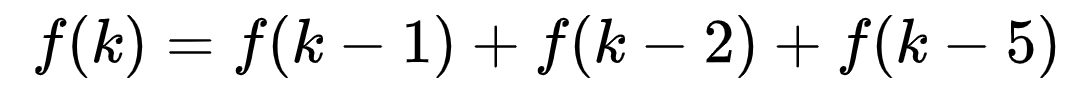
一定要理解：类似于走台阶和凑硬币的算法。
dp[1]+3 dp[2]+2 dp[3]+1 相当于往前走了一步，因此，dp[4]的结果应该是包含了所有可能的（dp[1]、dp[2]、dp[3]）

理解了这个，再设定一下系统的边界
f（0）=1

class Solution(object):
    def combinationSum4(self, coins, amount):
        dp = [0] * (amount + 1)
        dp[0] = 1  #凑出金额 0 的方案数为 1

        ## 全部的nums[0~i]中加出j，有多少种方法。
        ## 即对于nums的出现是有顺序关系的

        for j in range(1, amount + 1):   # 循环每一步dp[i]计算，相当于 遍历每一个 cnt
            for coin in coins:   #循环每一个数 找 f(k-1),f(k-2),f(k-5)
                if j >= coin:        # 防止以下情况: 例如当计算到dp[2] 时 计算 f(2-5) 出现负数
                    dp[j] += dp[j - coin]  #累加：f(k-1),f(k-2),f(k-5)

        return dp[-1] #返回最后一个值

s = Solution()
nums = [1,2,5]
target = 5
print(s.combinationSum4(nums,target))