动态规划LeetCode322零钱兑换

参考zzu_Lee https://www.cnblogs.com/hengzhezou/p/11042906.html 感谢

题目描述：

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

只有面额为 1元、2元、5元的三类硬币，每种数量无限。如果需要11元钱，最少的硬币数量是多少呢？
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1

示例 2:

只有面额为 2元的一类硬币，数量无限。如果需要3元钱，最少的硬币数量是多少呢？
输入: coins = [2], amount = 3
输出: -1
说明:某些数值，就是无法取出的。没有组合的方案。

思路一 ：贪心算法

贪心思想：直接先用最大面值的去减。

示例一

例如：面额为【1,2,5,10】，求14元
按照贪心思想：

  • 14-10=4
  • 4-2=2
  • 2-2=0
    则一共需要 10 2 2 三个硬币。

贪心思想成功了！！

示例二

例如：面额为【1,2,5,7,10】，求14元
如果利用贪心思想，应该是 10 2 2 三个硬币。
但是 7+7 2枚硬币，才是最优的答案。

因此贪心算法先天是有缺陷的

引入 动态规划 思想

动态规划的核心就是 寻找 状态转移方程

思路：
面额为【1,2,5】，求14元
首先 存储 0-13元之间的每一个最优解dp[i]
解释一下
dp[0]=0 需要0元的时候的结果
dp[1]=1 需要1元的时候，直接使用面额为1的1个硬币。结果为1
dp[2]=1 需要2元的时候，直接使用面额为2的1个硬币。结果为1
dp[3]=2 需要3元的时候，直接使用 面额为2的1个硬币 + 面额为1的1个硬币 。结果为2
dp[4]=2 需要4元的时候，直接使用 面额为2的2个硬币 。结果为2
dp[5]=1 需要5元的时候，直接使用 面额为5的1个硬币 。结果为1
dp[6]=2 需要6元的时候，直接使用 面额为1的1个硬币 + 面额为5的1个硬币 。结果为2
dp[7]=2 需要7元的时候，直接使用 面额为2的1个硬币 + 面额为5的1个硬币 。结果为2
dp[8]=3 需要8元的时候，直接使用 面额为1的1个硬币 + 面额为2的1个硬币 + 面额为5的1个硬币 。结果为3
dp[9]=3 需要9元的时候，直接使用 面额为2的2个硬币 + 面额为5的1个硬币 。结果为3
dp[10]=2 需要10元的时候，直接使用 面额为5的2个硬币 。结果为2
dp[11]=3 需要11元的时候，直接使用 面额为5的2个硬币 + 面额为1的1个硬币 。结果为3
dp[12]=3 需要12元的时候，直接使用 面额为5的2个硬币 + 面额为2的1个硬币 。结果为3
dp[13]=4 需要13元的时候，直接使用 面额为5的2个硬币 + 面额为2的1个硬币 + 面额为1的1个硬币。结果为4

dp[i]就是每一步的运算结果。动态规划的核心就是： 记录下每一步的结果，然后以递增的方式增加。

状态转移方程就是：

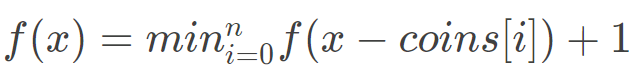
理解一下下一步 的思路

  • di[14]=min(di[14-1],di[14-2],di[14-5])+1
  • di[14]=min(di[13],di[12],di[9])+1
  • di[14]=min(4,3,3)+1
  • di[14]=4

文字解读一下：

相当于要求14元的时候，先看一下有哪些币种，【1,2,5】，
则 我们分别减去 后，为 dp[13],dp[12],dp[9],
（

  • 相当于在dp[13]状态时，加上一个1元的币；
  • 或 相当于在dp[12]状态时，加上一个2元的币；
  • 或 相当于在dp[9]状态时，加上一个5元的币；）
    再补上1个币。然后求他们的最小值。
    这里加1 ，其实应该在里面，不过经过公式推算，放在了外面。

对于那些无法计算得出的数值，直接记为 正无穷（因为我们是比较MIN值）

class Solution(object):
    def coinChange(self, coins, amount):
        """
        :type coins: List[int]
        :type amount: int
        :rtype: int
        """
        n = len(coins)
        # dp[i]表示amount=i需要的最少coin数
        dp = [float("inf")] * (amount+1)   # float("inf") 表示正无穷。初始化数组
        dp[0] = 0   #初始化第一个值记为0
        for i in range(amount+1):
            for coin in coins:
                # 只有当硬币面额不大于要求面额数时，才能取该硬币
                if coin <= i:
                    dp[i] = min(dp[i], dp[i-coin]+1)
        # 硬币数不会超过要求总面额数，如果超过，说明没有方案可凑到目标值
        return dp[amount] if dp[amount] <= amount else -1

posted on 2020-07-01 15:15  耀扬  阅读(297)  评论(0)  编辑  收藏  举报

导航