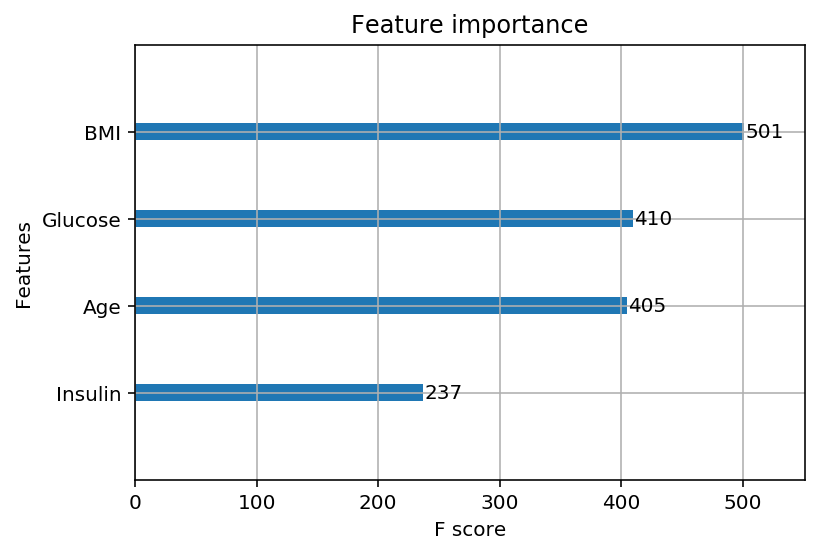最全模型实战Pima印第安人数据集上的机器学习-分类算法（逻辑回归、朴素贝叶斯、K近邻、决策树、支持向量机、xgboost、lightgbm）

本文主要参考自
爱吃串串的瘦子 https://blog.csdn.net/weixin_41988628/article/details/83051712
易悠 https://blog.csdn.net/yizheyouye/article/details/79791473
对部分内容进行了修正

最全模型实战Pima印第安人数据集上的机器学习-分类算法（逻辑回归、朴素贝叶斯、K近邻、决策树、支持向量机、xgboost、lightgbm）

1.数据集简介

该数据集最初来自国家糖尿病/消化/肾脏疾病研究所。数据集的目标是基于数据集中包含的某些诊断测量来诊断性的预测患者是否患有糖尿病。
从较大的数据库中选择这些实例有几个约束条件。尤其是，这里的所有患者都是Pima印第安至少21岁的女性。
数据集由多个医学预测变量和一个目标变量组成Outcome。预测变量包括患者的怀孕次数、BMI、胰岛素水平、年龄等。

import sys
import pandas as pd # 数据科学计算工具
import numpy as np # 数值计算工具
import matplotlib.pyplot as plt # 可视化
import seaborn as sns # matplotlib的高级API
import warnings
warnings.filterwarnings('ignore')

2 、加载数据并作图查看属性分布特征

【1】Pregnancies：怀孕次数
【2】Glucose：葡萄糖
【3】BloodPressure：血压 (mm Hg)
【4】SkinThickness：皮层厚度 (mm)
【5】Insulin：胰岛素 2小时血清胰岛素（mu U / ml
【6】BMI：体重指数（体重/身高）^2
【7】DiabetesPedigreeFunction：糖尿病谱系功能
【8】Age：年龄（岁）
【9】Outcome：类标变量（0或1）

pima = pd.read_csv("D:\\xgbtest\\pima-indians-diabetes.csv")

pima.head()

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BMI	DiabetesPedigreeFunction	Age	Outcome
0	6	148	72	35	0	33.6	0.627	50	1
1	1	85	66	29	0	26.6	0.351	31	0
2	8	183	64	0	0	23.3	0.672	32	1
3	1	89	66	23	94	28.1	0.167	21	0
4	0	137	40	35	168	43.1	2.288	33	1

pima.shape

(768, 9)

pima.describe()

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BMI	DiabetesPedigreeFunction	Age	Outcome
count	768.000000	768.000000	768.000000	768.000000	768.000000	768.000000	768.000000	768.000000	768.000000
mean	3.845052	120.894531	69.105469	20.536458	79.799479	31.992578	0.471876	33.240885	0.348958
std	3.369578	31.972618	19.355807	15.952218	115.244002	7.884160	0.331329	11.760232	0.476951
min	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.078000	21.000000	0.000000
25%	1.000000	99.000000	62.000000	0.000000	0.000000	27.300000	0.243750	24.000000	0.000000
50%	3.000000	117.000000	72.000000	23.000000	30.500000	32.000000	0.372500	29.000000	0.000000
75%	6.000000	140.250000	80.000000	32.000000	127.250000	36.600000	0.626250	41.000000	1.000000
max	17.000000	199.000000	122.000000	99.000000	846.000000	67.100000	2.420000	81.000000	1.000000

Data Visualization - 数据可视化

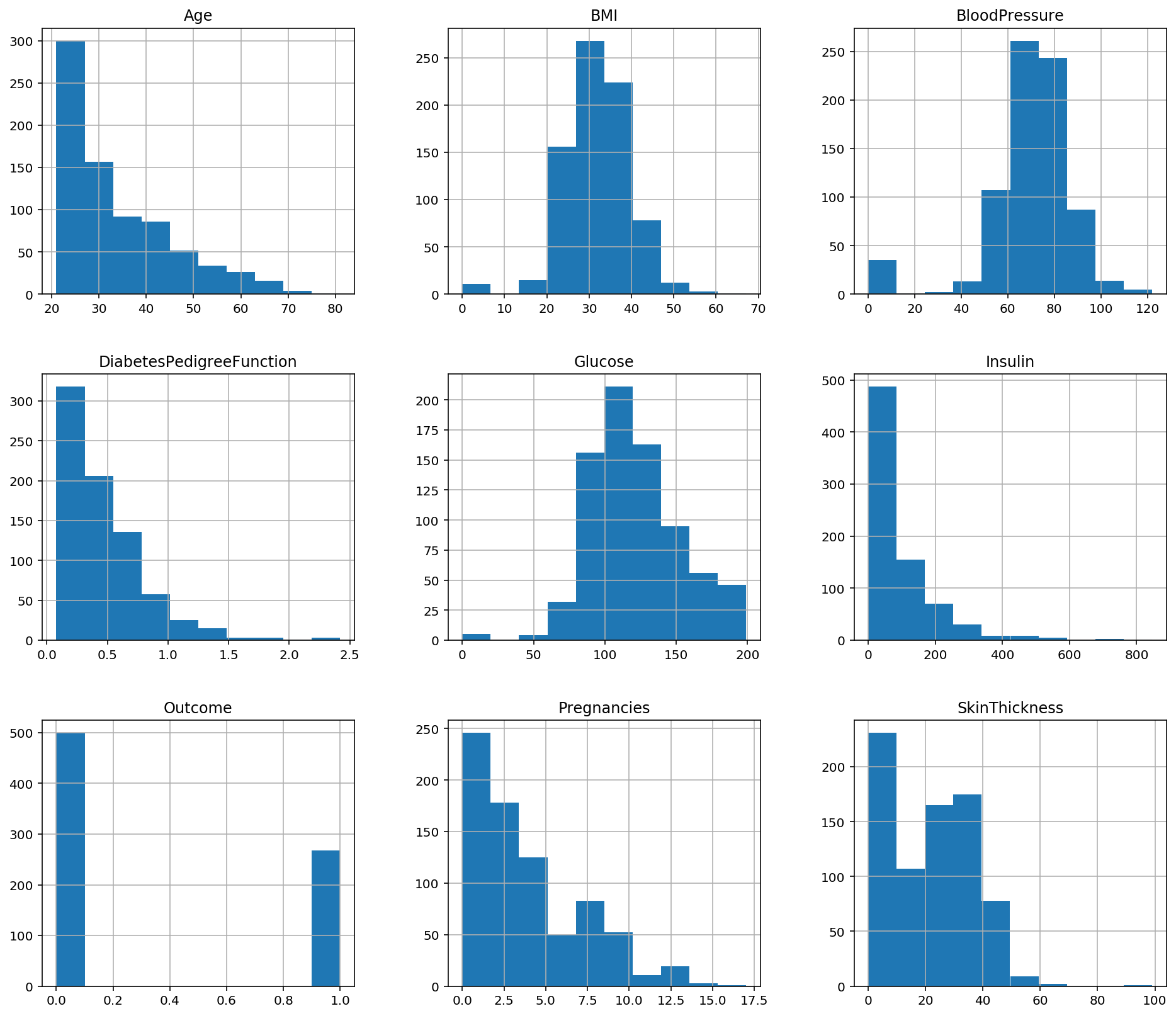
1.柱状图

pima.hist(figsize=(16,14)) #查看每个字段的数据分布；figsize的参数显示的是每个子图的长和宽

pima.hist(figsize=(16,14))

array([[<matplotlib.axes._subplots.AxesSubplot object at 0x0000022FB6DD9348>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x0000022FB6DE32C8>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x0000022FB6DA6448>],
       [<matplotlib.axes._subplots.AxesSubplot object at 0x0000022FBFF3A608>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x0000022FB6E0C348>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x0000022FBFF70788>],
       [<matplotlib.axes._subplots.AxesSubplot object at 0x0000022FBFF9CFC8>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x0000022FBFFD6848>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x0000022FBFFDD608>]],
      dtype=object)

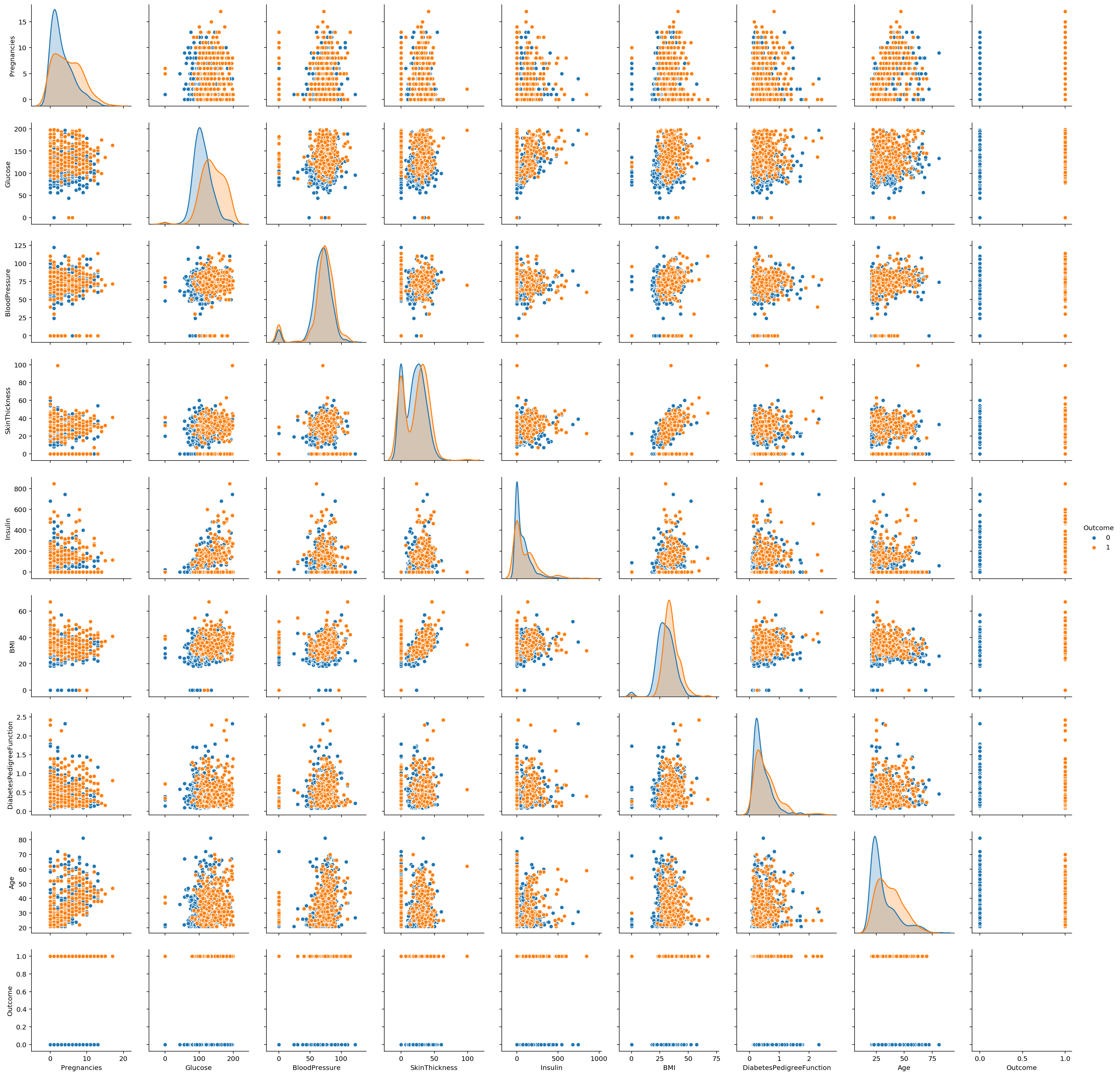
2.散点图

sns.pairplot(pima,hue='Outcome')

<seaborn.axisgrid.PairGrid at 0x22fc073d188>

seaborn常用命令

【1】set_style()是用来设置主题的，Seaborn有5个预设好的主题：darkgrid、whitegrid、dark、white、ticks，默认为darkgrid

【2】set()通过设置参数可以用来设置背景，调色板等，更加常用

【3】displot()为hist加强版

【4】kdeplot()为密度曲线图

【5】boxplot()为箱图

【6】joinplot()联合分布图

【7】heatmap()热点图

【8】pairplot()多变量图，可以支持各种类型的变量分析，是特征分析很好用的工具

3.箱图

pandas.plot作图：数据分为Series 和 DataFrame两种类型；现释义数据为DataFrame的参数

【0】data:DataFrame

【1】x:label or position,default None 指数据框列的标签或位置参数

【2】y:label or position,default None 指数据框列的标签或位置参数

【3】kind:str（line折线图、bar条形图、barh横向条形图、hist柱状图、
box箱线图、kde Kernel的密度估计图，主要对柱状图添加Kernel概率密度线、
density same as “kde”、area区域图、pie饼图、scatter散点图、hexbin）

【4】subplots:boolean，default False，为每一列单独画一个子图

【5】sharex:boolean，default True if ax is None else False

【6】sharey:boolean,default False

【7】loglog:boolean,default False,x轴/y轴同时使用log刻度

pima.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False, figsize=(16,14))

Pregnancies                    AxesSubplot(0.125,0.657941;0.227941x0.222059)
Glucose                     AxesSubplot(0.398529,0.657941;0.227941x0.222059)
BloodPressure               AxesSubplot(0.672059,0.657941;0.227941x0.222059)
SkinThickness                  AxesSubplot(0.125,0.391471;0.227941x0.222059)
Insulin                     AxesSubplot(0.398529,0.391471;0.227941x0.222059)
BMI                         AxesSubplot(0.672059,0.391471;0.227941x0.222059)
DiabetesPedigreeFunction          AxesSubplot(0.125,0.125;0.227941x0.222059)
Age                            AxesSubplot(0.398529,0.125;0.227941x0.222059)
Outcome                        AxesSubplot(0.672059,0.125;0.227941x0.222059)
dtype: object

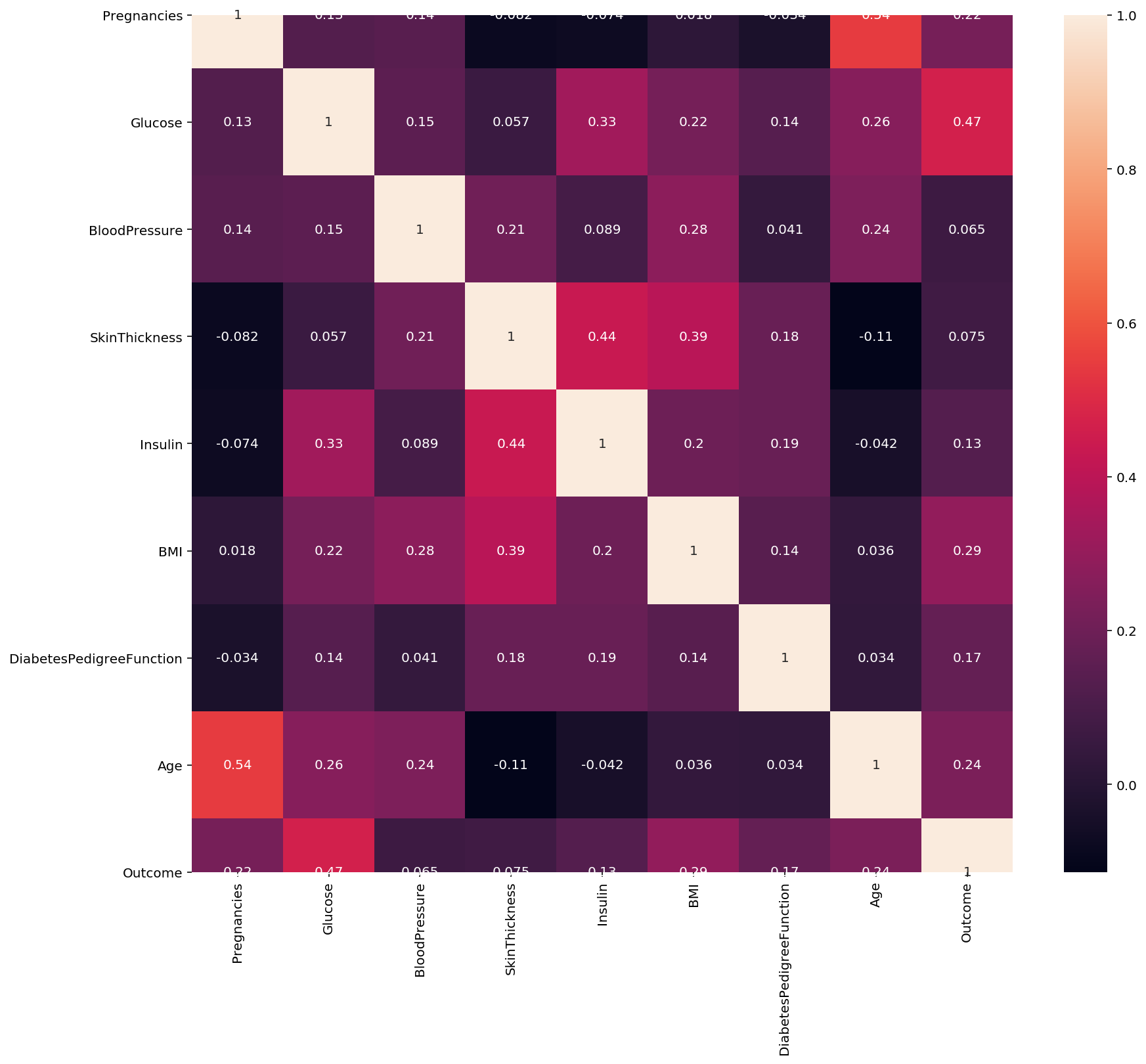
4.热度图

column_x = pima.columns[0:len(pima.columns) - 1] # 选择特征列，去掉目标列
 
column_x # 显示所有特征列信息
 
corr = pima[pima.columns].corr() # 计算变量的相关系数，得到一个N * N的矩阵
 
plt.subplots(figsize=(14,12)) # 可以先试用plt设置画布的大小，然后在作图，修改
sns.heatmap(corr, annot = True) # 使用热度图可视化这个相关系数矩阵

<matplotlib.axes._subplots.AxesSubplot at 0x22fc5906608>

3、数据预处理——特征工程

3.1、特征选择

导入和特征选择相关的包

评分函数

1.SelectKBest() #只保留K个最高分的特征，能够返回特征评价的得分 SelectKBest(score_func=, k=10)

2.SelectPercentile() #只保留用户指定百分比的最高得分的特征，能够返回特征评价的得分 SelectPercentile(score_func=, percentile=10)
使用常见的单变量统计检验：假正率SelectFpr，错误发现率SelectFdr，或者总体错误率SelectFwe

3.GenericUnivariateSelect() #通过结构化策略进行特征选择，通过超参数搜索估计器进行特征选择

将特征输入到评分函数，返回一个单变量的f_score(F检验的值)或p-values(P值，假设检验中的一个标准，P-value用来和显著性水平作比较)，
注意SelectKBest 和 SelectPercentile只有得分，没有p-value。
其中的参数score_func有以下选项：

【1】回归：f_regression:相关系数，计算每个变量与目标变量的相关系数，然后计算出F值和P值
mutual_info_regression:互信息，互信息度量X和Y共享的信息：
它度量知道这两个变量其中一个，对另一个不确定度减少的程度。

【2】分类：chi2：卡方检验
f_classif:方差分析，计算方差分析（ANOVA）的F值（组间均方/组内均方）；
mutual_info_classif:互信息，互信息方法可以捕捉任何一种统计依赖，但是作为非参数法，需要更多的样本进行准确的估计。

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
 
X = pima.iloc[:, 0:8] # 特征列 0-7列，不含第8列
Y = pima.iloc[:, 8] # 目标列为第8列
 
select_top_4 = SelectKBest(score_func=chi2, k =4) # 通过卡方检验选择4个得分最高的特征
fits = select_top_4.fit(X, Y) #将特征输入到评分函数，获取特征信息和目标值信息
features = fits.transform(X) #展现特征转换后的结果
fits.get_support(indices=True).tolist()  #得到宣传的相关性排名前4的列[1,4,5,7]
# 因此，表现最佳的特征是：Glucose-葡萄糖、Insulin-胰岛素、BMI指数、Age-年龄
# features[0:5] #新特征列

[1, 4, 5, 7]

3.1 构造新特征DataFrame

X_features = pd.DataFrame(data = features, columns=["Glucose","Insulin","BMI","Age"]) # 构造新特征DataFrame
Y_features = pd.DataFrame(data = Y, columns=["Outcome"]) 
# 构造新特征DataFrame

3.2、 Standardization - 标准化

它将属性值更改为均值为0，标准差为1 的高斯分布. 当算法期望输入特征处于高斯分布时，它非常有用

from sklearn.preprocessing import StandardScaler 
rescaledX = StandardScaler().fit_transform(X_features)
#通过sklearn的preprocessing数据预处理中StandardScaler特征缩放 标准化特征信息 
X = pd.DataFrame(data = rescaledX, columns = X_features.columns)
 # 构建新特征DataFrame 
X.head()

	Glucose	Insulin	BMI	Age
0	0.848324	-0.692891	0.204013	1.425995
1	-1.123396	-0.692891	-0.684422	-0.190672
2	1.943724	-0.692891	-1.103255	-0.105584
3	-0.998208	0.123302	-0.494043	-1.041549
4	0.504055	0.765836	1.409746	-0.020496

3.3、将数据集切分——训练集和测试集

from sklearn.model_selection import train_test_split
 
seed = 7 #重现随机生成的训练
test_size = 0.33 #33%测试，67%训练
X_train, X_test, Y_train, Y_test = train_test_split(X, Y_features, test_size=test_size, random_state=seed)

4、构建二分类算法模型

from sklearn.model_selection import KFold,StratifiedKFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from xgboost import XGBClassifier
from lightgbm import LGBMClassifier

models = []
models.append(("LR", LogisticRegression())) #逻辑回归
models.append(("NB", GaussianNB())) # 高斯朴素贝叶斯
models.append(("KNN", KNeighborsClassifier())) #K近邻分类
models.append(("DT", DecisionTreeClassifier())) #决策树分类
models.append(("SVM", SVC())) # 支持向量机分类
models.append(("xgboost", XGBClassifier())) #xgboost分类
models.append(("lightgbm", LGBMClassifier())) #lightgbm分类

cross_val_score()函数

sklearn.cross_validation.cross_val_score(estimator, X, y=None, scoring=None, cv=None, n_jobs=1, verbose=0, fit_params=None, pre_dispatch='2*n_jobs')

参数

estimator：数据对象

X：数据

y：预测数据

soring：调用的方法

cv：交叉验证生成器或可迭代的次数

n_jobs：同时工作的cpu个数（-1代表全部）

verbose：详细程度

fit_params：传递给估计器的拟合方法的参数

pre_dispatch：控制并行执行期间调度的作业数量。

KFold——K折交叉验证：

这是将数据集分成K份的官方给定方案，所谓K折就是将数据集通过K次分割，使得所有数据既在训练集出现过，又在测试集出现过，当然，每次分割中不会有重叠。相当于无放回抽样。

StratifiedKFold用法类似Kfold，但是他是分层采样，确保训练集，测试集中各类别样本的比例与原始数据集中相同。

sklearn.model_selection.KFold(n_splits=3, shuffle=False, random_state=None)

思路：将训练/测试数据集划分n_splits个互斥子集，每次用其中一个子集当作验证集，剩下的n_splits-1个作为训练集，进行n_splits次训练和测试，得到n_splits个结果

注意点：对于不能均等份的数据集，其前n_samples % n_splits子集拥有n_samples // n_splits + 1个样本，其余子集都只有n_samples // n_splits样本

参数说明：

n_splits：表示划分几等份

shuffle：在每次划分时，是否进行洗牌

①若为Falses时，其效果等同于random_state等于整数，每次划分的结果相同

②若为True时，每次划分的结果都不一样，表示经过洗牌，随机取样的

random_state：随机种子数

属性：

①get_n_splits(X=None, y=None, groups=None)：获取参数n_splits的值

②split(X, y=None, groups=None)：将数据集划分成训练集和测试集，返回索引生成器

results = []
names = []
for name, model in models:
    kflod = KFold(n_splits=10, random_state=22)
    cv_result = cross_val_score(model, X_train,Y_train, cv = kflod,scoring="accuracy")
    names.append(name)
    results.append(cv_result)

for i in range(len(names)):
    print(names[i], results[i].mean())

LR 0.7505656108597286
NB 0.7604449472096532
KNN 0.7292986425339366
DT 0.7177224736048267
SVM 0.760369532428356
xgboost 0.7565987933634993
lightgbm 0.748868778280543

不同模型下的可视化结果

1.盒图:

ax = sns.boxplot(data = results)
ax.set_xticklabels(names)

[Text(0, 0, 'LR'),
 Text(0, 0, 'NB'),
 Text(0, 0, 'KNN'),
 Text(0, 0, 'DT'),
 Text(0, 0, 'SVM'),
 Text(0, 0, 'xgboost'),

Text(6.5, 0, 'lightgbm')]

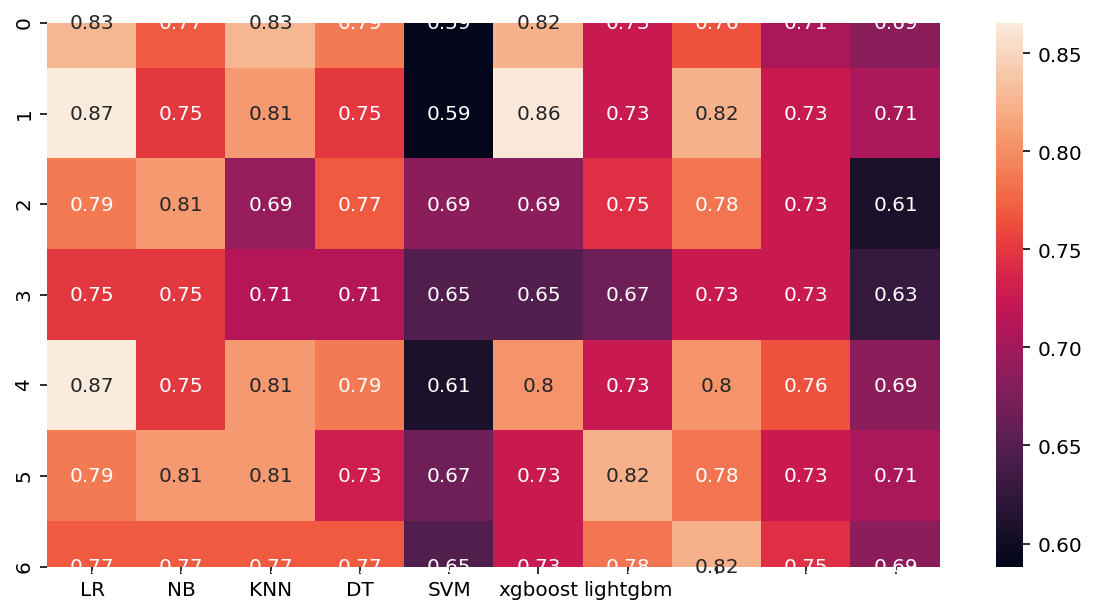
2.热力图

plt.subplots(figsize=(10,5)) # 可以先试用plt设置画布的大小，然后在作图，修改
ax = sns.heatmap(data = results,annot = True)
ax.set_xticklabels(names)

[Text(0.5, 0, 'LR'),
 Text(1.5, 0, 'NB'),
 Text(2.5, 0, 'KNN'),
 Text(3.5, 0, 'DT'),
 Text(4.5, 0, 'SVM'),
 Text(5.5, 0, 'xgboost'),

Text(0, 0, 'lightgbm')]

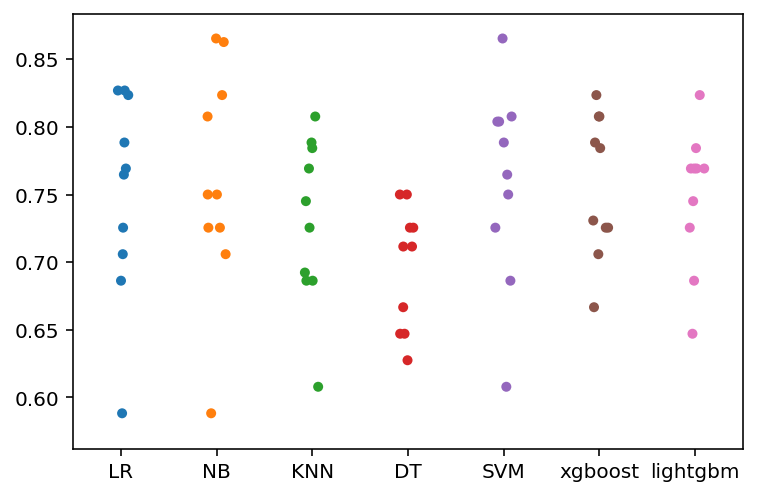
3.散点图

ax = sns.stripplot(data = results)
ax.set_xticklabels(names)

[Text(0, 0, 'LR'),
 Text(0, 0, 'NB'),
 Text(0, 0, 'KNN'),
 Text(0, 0, 'DT'),
 Text(0, 0, 'SVM'),
 Text(0, 0, 'xgboost'),

Text(0, 0, 'lightgbm')]

4.小提琴图：

中间的白点是中位数，黑色粗线对应分位数

ax = sns.violinplot(data = results)
ax.set_xticklabels(names)

[Text(0, 0, 'LR'),
 Text(0, 0, 'NB'),
 Text(0, 0, 'KNN'),
 Text(0, 0, 'DT'),
 Text(0, 0, 'SVM'),
 Text(0, 0, 'xgboost')]

5、模型评估（参数选择）

1.PCA SVM

from sklearn.decomposition import KernelPCA

kpca = KernelPCA(n_components = 2, kernel = 'rbf')  #kernel = 'rbf' 核函数为 高斯核函数，n_components:降维后的维数 2维
X_train_pca = kpca.fit_transform(X_train)  #fit_transform(trainData)对部分数据先拟合fit，找到该part的整体指标，如均值、方差、最大值最小值等等（根据具体转换的目的），然后对该trainData进行转换transform，从而实现数据的标准化、归一化等等。
X_test_pca = kpca.transform(X_test)

from sklearn.svm import SVC
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.model_selection import GridSearchCV


classifier = SVC(kernel = 'rbf')
classifier.fit(X_train_pca, Y_train)

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
    kernel='rbf', max_iter=-1, probability=False, random_state=None,
    shrinking=True, tol=0.001, verbose=False)

参数：

C：C-SVC的惩罚参数C 默认值是1.0

C越大，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’

0 – 线性：u'v
1 – 多项式：(gammau'v + coef0)^degree
2 – RBF函数：exp(-gamma|u-v|^2)
3 –sigmoid：tanh(gammau'v + coef0)

degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。

gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features

coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。

probability ：是否采用概率估计？.默认为False

shrinking ：是否采用shrinking heuristic方法，默认为true

tol ：停止训练的误差值大小，默认为1e-3

cache_size ：核函数cache缓存大小，默认为200

class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)

verbose ：允许冗余输出？

max_iter ：最大迭代次数。-1为无限制。

decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None3

random_state ：数据洗牌时的种子值，int值

主要调节的参数有：C、kernel、degree、gamma、coef0。

2.xgboost

xgb1 = XGBClassifier(
    learning_rate = 0.1,
    n_estimators = 1000,
    max_depth = 5,
    min_child_weight = 1,
    gamma = 0,
    subsample = 0.8,
    colsample_bytree = 0.8,
    objective = 'binary:logistic',
    nthread = 4,
    scale_pos_weight = 1,
    seed = 27
    )

model = XGBClassifier()               
learning_rate = [0.0001,0.001,0.01,0.1,0.2,0.3] #学习率
gamma = [1, 0.1, 0.01, 0.001]
 
param_grid = dict(learning_rate = learning_rate,gamma = gamma) #转化为字典格式，网络搜索要求
 
kflod = StratifiedKFold(n_splits=10, shuffle = True,random_state=7) #将训练/测试数据集划分10个互斥子集， StratifiedKFold用法类似Kfold，但是他是分层采样，确保训练集，测试集中各类别样本的比例与原始数据集中相同。

grid_search = GridSearchCV(model,param_grid,scoring = 'neg_log_loss',n_jobs = -1,cv = kflod)

#scoring指定损失函数类型，n_jobs指定全部cpu跑，cv指定交叉验证

grid_result = grid_search.fit(X_train_pca, Y_train) #运行网格搜索

print("Best: %f using %s" % (grid_result.best_score_,grid_search.best_params_))
print('穷举后 最优的参数: ',grid_search.best_estimator_) 
#best_params_：描述了已取得最佳结果的参数的组合
#best_score_：成员提供优化过程期间观察到的最好的评分
#具有键作为列标题和值作为列的dict，可以导入到DataFrame中。
#注意，“params”键用于存储所有参数候选项的参数设置列表。

# 打印分析的过程
# means = grid_result.cv_results_['mean_test_score']
# params = grid_result.cv_results_['params']
# for mean,param in zip(means,params):
#     print("%f  with:   %r" % (mean,param))

Best: -0.564962 using {'gamma': 1, 'learning_rate': 0.1}
穷举后 最优的参数:  XGBClassifier(base_score=0.5, booster=None, colsample_bylevel=1,
              colsample_bynode=1, colsample_bytree=1, gamma=1, gpu_id=-1,
              importance_type='gain', interaction_constraints=None,
              learning_rate=0.1, max_delta_step=0, max_depth=6,
              min_child_weight=1, missing=nan, monotone_constraints=None,
              n_estimators=100, n_jobs=0, num_parallel_tree=1,
              objective='binary:logistic', random_state=0, reg_alpha=0,
              reg_lambda=1, scale_pos_weight=1, subsample=1, tree_method=None,
              validate_parameters=False, verbosity=None)

GridSearchCV 相关参数

初始化了一个GridSearchCV对象，用于对支持向量机流水线的训练与调优。将GridSearchCV的param_grid参数以字典的方式定义为待调优参数。

（1）estimator

选择使用的分类器，并且传入除需要确定最佳的参数之外的其他参数。每一个分类器都需要一个scoring参数，或者score方法：estimator=RandomForestClassifier(min_samples_split=100,min_samples_leaf=20,max_depth=8,max_features='sqrt',random_state=10),

（2 param_grid

需要最优化的参数的取值，值为字典或者列表，例如：param_grid =param_test1，param_test1 = {'n_estimators':range(10,71,10)}。

（3）scoring=None

模型评价标准，默认None,这时需要使用score函数；或者如scoring='roc_auc'，根据所选模型不同，评价准则不同。字符串（函数名），或是可调用对象，需要其函数签名形如：scorer(estimator, X, y)；如果是None，则使用estimator的误差估计函数。具体值的选取看本篇第三节内容。

（4）fit_params=None

（5） n_jobs=1

n_jobs: 并行数，int：个数,-1：跟CPU核数一致, 1:默认值

进行预测的常用方法和属性

grid.fit()：运行网格搜索

grid_scores_：给出不同参数情况下的评价结果

best_params_：描述了已取得最佳结果的参数的组合

best_score_：提供优化过程期间观察到的最好的评分

cv_results_ : dict of numpy (masked) ndarrays

具有键作为列标题和值作为列的dict，可以导入到DataFrame中。注意，“params”键用于存储所有参数候选项的参数设置列表。

运用调好参数的模型正式训练数据

classifier = XGBClassifier(
    learning_rate = 0.1,
    n_estimators = 1000,
    max_depth = 5,
    min_child_weight = 1,
    gamma = 1,
    subsample = 0.8,
    colsample_bytree = 0.8,
    objective = 'binary:logistic',
    nthread = 4,
    scale_pos_weight = 1,
    seed = 27
    )
classifier.fit(X_train_pca, Y_train)

XGBClassifier(base_score=0.5, booster=None, colsample_bylevel=1,
              colsample_bynode=1, colsample_bytree=0.8, gamma=1, gpu_id=-1,
              importance_type='gain', interaction_constraints=None,
              learning_rate=0.1, max_delta_step=0, max_depth=5,
              min_child_weight=1, missing=nan, monotone_constraints=None,
              n_estimators=1000, n_jobs=4, nthread=4, num_parallel_tree=1,
              objective='binary:logistic', random_state=27, reg_alpha=0,
              reg_lambda=1, scale_pos_weight=1, seed=27, subsample=0.8,
              tree_method=None, validate_parameters=False, verbosity=None)

5.1.详细评估

classification_report

y_pred = classifier.predict(X_test_pca)   #输入测试数据 的到 y的 预测值

cm = confusion_matrix(Y_test, y_pred)#混淆矩阵
cm

array([[132,  30],
       [ 47,  45]], dtype=int64)

结果说明：把0预测成0的有132个，把0预测成1的有30个，把1预测成0的有47个，把1预测成1的有55个。

print(classification_report(Y_test, y_pred))#显示准确率

              precision    recall  f1-score   support

           0       0.74      0.81      0.77       162
           1       0.60      0.49      0.54        92

    accuracy                           0.70       254
   macro avg       0.67      0.65      0.66       254
weighted avg       0.69      0.70      0.69       254

准确率：精确率是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。

所有识别为”1”的数据中，正确的比率是多少。

如上题识别出来178个结果是“0”，而只有132个结果正确，有47个实现是非“0”的数据。所以准确率就为74%

召回率：召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了

所有样本为1的数据中，最后真正识别出1的比率。

如上题162个样本”0”, 只识别出了132个是“0”，其它30个是识别成了其它数据。所以召回率是81%

F1-score:

是准确率与召回率的综合。可以认为是平均效果。

F1值是精确度和召回率的调和平均值：2F1=1P+1R 2F1=1P+1R F1=2P×RP+R F1=2P×RP+R
精确度和召回率都高时， F1 F1值也会高． F1 F1值在1时达到最佳值（完美的精确度和召回率），最差为0．在二元分类中， F1 F1值是测试准确度的量度。

例子：当一个搜索引擎返回30个页面时，只有20页是相关的，而没有返回40个额外的相关页面，其精度为20/30 = 2/3，而其召回率为20/60 = 1/3。在这种情况下，精确度是“搜索结果有多大用处”，而召回是“结果如何完整”。

详细定义如下：

对于数据测试结果有下面4种情况：

TP: 预测为正，实现为正

FP: 预测为正，实现为负

FN: 预测为负，实现为正

TN: 预测为负，实现为负

准确率： TP/ (TP+FP)

召回率： TP(TP + FN)

F1-score: 2TP/(2TP + FP + FN)

一般（粗）评估——accuracy_score

sklearn.metrics.accuracy_score(y_true, y_pred, normalize=True, sample_weight=None)

分类准确率分数是指所有分类正确的百分比。分类准确率这一衡量分类器的标准比较容易理解，但是它不能告诉你响应值的潜在分布，并且它也不能告诉你分类器犯错的类型。

normalize：默认值为True，返回正确分类的比例；如果为False，返回正确分类的样本数

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(Y_test, y_pred) #显示准确率——分类0和1的total
print("Accuracy: %.2f%%" % (accuracy * 100.0))

Accuracy: 69.69%

判断比较不同特征的重要程度

#判断特征的重要程度
from xgboost import plot_importance
from matplotlib import pyplot

#使用XGBoost进行训练
model = XGBClassifier()
model.fit(X_train,Y_train)

# 绘制重要性曲线,max_num_feature参数设置输出前20重要的特征（）
plot_importance(model,max_num_features=20)
plt.show()

posted on 2020-03-02 21:32 耀扬阅读(1966) 评论(0) 编辑收藏举报

刷新页面返回顶部

耀扬

最全模型实战Pima印第安人数据集上的机器学习-分类算法（逻辑回归、朴素贝叶斯、K近邻、决策树、支持向量机、xgboost、lightgbm）

最全模型实战Pima印第安人数据集上的机器学习-分类算法（逻辑回归、朴素贝叶斯、K近邻、决策树、支持向量机、xgboost、lightgbm）

1.数据集简介

2 、加载数据并作图查看属性分布特征

Data Visualization - 数据可视化

1.柱状图

2.散点图

seaborn常用命令

3.箱图

pandas.plot作图：数据分为Series 和 DataFrame两种类型；现释义数据为DataFrame的参数

4.热度图

3、数据预处理——特征工程

3.1、特征选择

3.1 构造新特征DataFrame

3.2、 Standardization - 标准化

3.3、将数据集切分——训练集和测试集

4、构建二分类算法模型

cross_val_score()函数

sklearn.cross_validation.cross_val_score(estimator, X, y=None, scoring=None, cv=None, n_jobs=1, verbose=0, fit_params=None, pre_dispatch='2*n_jobs')

KFold——K折交叉验证：

不同模型下的可视化结果

1.盒图:

2.热力图

3.散点图

4.小提琴图：

5、模型评估（参数选择）

1.PCA SVM

2.xgboost

GridSearchCV 相关参数

进行预测的常用方法和属性

运用调好参数的模型正式训练数据

5.1.详细评估

classification_report

一般（粗）评估——accuracy_score

判断比较不同特征的重要程度

导航

公告

耀扬

最全模型实战Pima印第安人数据集上的机器学习-分类算法（逻辑回归、朴素贝叶斯、K近邻、决策树、支持向量机、xgboost、lightgbm）

最全模型实战Pima印第安人数据集上的机器学习-分类算法（逻辑回归、朴素贝叶斯、K近邻、决策树、支持向量机、xgboost、lightgbm）

1.数据集简介

2 、加载数据并作图查看属性分布特征

Data Visualization - 数据可视化

1.柱状图

2.散点图

seaborn常用命令

3.箱图

pandas.plot作图：数据分为Series 和 DataFrame两种类型；现释义数据为DataFrame的参数

4.热度图

3、 数据预处理——特征工程

3.1、特征选择

3.1 构造新特征DataFrame

3.2、 Standardization - 标准化

3.3、将数据集切分——训练集和测试集

4、 构建二分类算法模型

cross_val_score()函数

sklearn.cross_validation.cross_val_score(estimator, X, y=None, scoring=None, cv=None, n_jobs=1, verbose=0, fit_params=None, pre_dispatch='2*n_jobs')

KFold——K折交叉验证：

不同模型下的可视化结果

1.盒图:

2.热力图

3.散点图

4.小提琴图：

5、模型评估（参数选择）

1.PCA SVM

2.xgboost

GridSearchCV 相关参数

进行预测的常用方法和属性

运用调好参数的模型正式训练数据

5.1.详细评估

classification_report

一般（粗）评估——accuracy_score

判断比较不同特征的重要程度

导航

公告

3、数据预处理——特征工程

4、构建二分类算法模型