应用统计学习笔记2
第一部分:抽样
常用概念
残差:
F值是F检验的统计量值 。F检验是一种在零假设(null hypothesis, H0)之下,统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型,以判断该模型中的全部或一部分参数是否适合用来估计母体。
相关系数:
Pearson相关系数(Pearson CorrelationCoefficient)是用来衡量两个数据集合是否在一条线上面,它用来衡量定距变量间的线性关系。
spearman相关系数, 以查尔斯·斯皮尔曼命名的斯皮尔曼等级相关系数,即spearman相关系数。经常用希腊字母ρ表示。 它是衡量两个变量的依赖性的 非参数 指标。 它利用单调方程评价两个统计变量的相关性。 如果数据中没有重复值, 并且当两个变量完全单调相关时,斯皮尔曼相关系数则为+1或−1。
kendall秩相关系数(R)是指设有n个统计对象,每个对象有两个属性的系数。将所有统计对象按属性1取值排列,不失一般性,设此时属性2取值的排列是乱序的。设P为两个属性值排列大小关系一致的统计对象对数。
卡方统计量 是指数据的分布与所选择的预期或假设分布之间的差异的度量。在1900年由英国统计学家pearson提出,是用于卡方检验中的一个统计量。它可用于检验类别变量之间的独立性或确定关联性。例如,如果有一个按投票者性别分类的选举结果的双因子表,卡方统计量可帮助确定投票是否独立于投票者的性别,或者在投票与性别之间是否存在关联。如果与卡方统计量相关联的p值小于选定的a水平,检验将拒绝两个变量彼此独立的原假设。
卡方检验 就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,表明理论值完全符合。





正态分布的几何特征
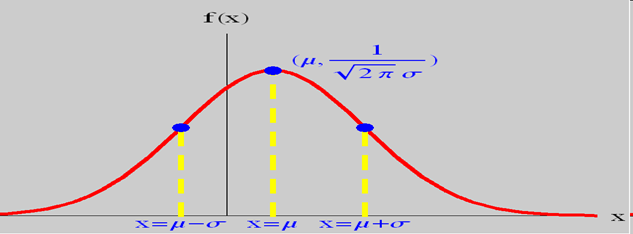


标准正态分布

1、正态总体,σ为已知

2、非正态总体,σ为已知
从某地区统计中得知,该地区郊区平均每一家庭年收入为3160元,标准差为800元。从此郊区抽取50个家庭为一随机样本,平均每年收入为以下数字的平均概率是多少:(1)多于3000元;(2)少于3000元;(3)在3200元到3300元之间(4)样本家庭收入![]() 能以0.99的概率落在其中的取件。
能以0.99的概率落在其中的取件。
3、正态总体,σ为未知
假定该地区郊区每一个家庭年收入服从正态分布,均值μ为3160元,σ未知。现任取一样本,容量为16.样本平均年收入![]() 为3040元,样本标准差S为240元。试问,在抽样时取到平均收入不大于3040元的样本的概率有多大?
为3040元,样本标准差S为240元。试问,在抽样时取到平均收入不大于3040元的样本的概率有多大?
样本比率的抽样分布
所要研究的特征只有两个可能的结果,此时样本中的每个数据只代表两个状态。
假定某厂生产的产品中次品率为3%。现抽取一个n=400的随机样本,问样本中次品所占的比率![]() 小于3.5%的概率有多大?
小于3.5%的概率有多大?
第二部分 参数估计
就是用样本统计量去估计总体的参数
遇到不知道μ和σ2的值的问题时,要估计出μ和σ2的值 或 范围 的题
根据一个抽出的随机样本计算的平均分数为80分,我们就用80分作为全班考试成绩的平均分数的一个估计值,这就是点估计。
要估计一批产品的合格率,根据抽样结果合格率为96%,将96%直接作为这批产品合格率的估计值,这也是点估计
从某城市中抽取1000户职工家庭作为样本, 根据样本的资料估计出该城市全体职工家庭每人全年收入的平均4000元,这种以点带面的估计方法称之点估计
特征数法,用样本的特征数估计总体特征数的方法
例题:已知某种灯泡的寿命X - N(μ,σ2),其中μ、σ2都是未知的,今随机取得5只灯泡,测得寿命(单位:小时)为1512、1495、1530、1501、1462,试估计这批灯泡寿命的分布。
极大似然估计法:利用总体的分布密度或概率分布的表达式机器样本所提供的信息建立起求未知参数估计量的一种方法。
“似然” 就是 “可能”!“极大似然”就是“最大可能性”!!!!!!这就是中国人瞎拽词,坑的自己人!
极大似然估计的思想:“概率最大的事件最有可能发生”
正态总体参数的区间估计
“置信”这个词也是中国人坑中国人,“置信”就是“可信”。
举例说明:经过统计分析,姚明每场比赛能够拿到的分数为15—38分,这个结论的把握程度为95%。这个把握程度就是置信度(95%)。这个分数段(15—38分)就是与此置信度相对应的置信区间。有多少个置信度,就是多少个置信区间,或者反之。
正态总体均值的区间估计
单个正态总体均值μ的区间估计
例题:
某机械厂生产的某种产品的长度X服从正态分布 。现从这批产品中随机抽取6件,测得其长度(cm)如下:
14.50 15.21 15.33 15.01 15.12 15.13
分别在下面两种情况下,求该批产品长度的置信区间,置信度为0.95。
例题:
某大学从该校学生中随机抽取100人,调查他们平均每人每天完成作业时间未120min,样本标准差为30min。试以95%的置信水平估计该大学全体学生平均每天完成作业时间。
两个正态总体均值差的区间估计
例题
单个总体方差σ2的区间估计
在现实问题中,我们经常还需要对作为衡量变量偏离总体平均数尺度的方差进行估计,例如一批电池的平均使用寿命虽然合乎要求,但若个电池之间寿命相差很大及方差很大,那么这批电池的质量还是有问题,因此我们需要知道总体方差和标准差的大小
例题:对电池厂生产的一批电池进行使用寿命实验,现抽取20个样本测得S=6小时,假设电池寿命服从正态分布,试求总体标准差σ的置信度为0.95的置信区间。
两个总体方差比的区间估计
在实际工作中,我们常会遇到比较两个总体的方差问题,例如比较两台机器生产过程的稳定性,两种计量工具的精度等,这实质上都是对两个总体的方差进行比较。
例题:为了测定甲乙两厂生产的某种材料的拉力强度,现从甲厂抽取25个样品,测得样本方差等于26.5,从乙厂抽取30个样品,测得样本方差等于18.1设两样本相互独立,且拉力强度服从正态分布,试求方差比的置信度为0.9的置信区间
总体比率的区间估计
总体比率的区间估计
在许多实际问题中,常常需要估计总体中具有某种特征的单位占总体全部单位的比率。例如企业检验人员想知道,本企业全部产品中 合格品的比率;商店经理想了解对他们服务满意的顾客,在全部顾客中所占的比率等
例题:在一大批产品中,抽查80件,结果其中有35件是一级品,求该批产品一级品率的置信区间。
两个总体比率之差的区间估计
在许多实际问题中,常常需要估计总体中具有某种特征的单位占总体全部单位的比率。例如企业检验人员想知道,本企业全部产品中 合格品的比率;商店经理想了解对他们服务满意的顾客,在全部顾客中所占的比率等
例题:某公司下属有两个电子元件厂,为了提高产品的一级品率,该公司对甲厂的工人进行了业务培训。一个月后,公司质检部对两个厂的产品进行了检验。从甲厂抽取了300件,测得一级品为195件。从乙厂抽取了400件,测得一级品为220件。试求甲、乙两厂产品一级品率P1-P2的置信度为0.95的置信区间。
单侧置信区间
以上讨论的区间估计都是双侧的,但在某些实际问题中,例如产品的次品率设备元件的使用寿命等,我们只对他的某一侧感兴趣。如灯泡的寿命平均寿命长,是我们所希望的。我们关心的是平均寿命不要过短,即他的“下限”。反之,在考虑产品的次品率是显然次品率越低越好,而我们关注的是其“上限”不要过大,这就引出了单侧置信区间的概念
例题:在一批进口的彩色显像管中,随机的抽取六只做寿命测试,其寿命分别为(单位:h)
17600 18700 19100 16800 185 17300
设显像管寿命服从正态分布,试求其寿命的平均值μ的置信度为0.95具有置信下限的置信区间。
样本容量的确定
通俗的说,就是我想要调查,应该抽取多少样本数量,才能保证统计结果合理。
一家市场调研公司想估计某地区有彩色电视机的家庭所占的比例。该公司希望对比例p的估计误差不超过0.05,要求的可靠程度为95%,应抽多大容量的样本(没有可利用的p估计值)。
第三部分 假设检验
假设检验:根据样本的信息检验关于总体的某个假设是否正确。通俗的说就是 先假设,再验证!
假设检验的主要方法:逻辑上运用反证法,统计上依据小概率原理
实际工作中常会遇到这样的问题:
(1)某产品在改进工艺后的次品率是否有下降?
(2)假定总体服从某种分布是否成立?
(3)检验新产品的性能是否有显著提高?
(4)在产品质量检验中,将样本的不合格率与规定的不合格率界限进行比较,是否有明显差距。
第四部分 方差分析
实际问题
1、有几种不同的原料需考察它们对产品的质量有无显著的影响?
2、几个检验员检验同一种产品,想了解它们检验技术水平的高低?
3、不同颜色的同种饮料,想了解饮料的颜色是否对销售量产生影响?
4、学生家庭的职业背景是否对学生的学业带来影响?
方差分析(Analysis of variance,ANOVA)的主要目的是通过对方差的比较来检验多个均值之间差异的显著性。


