机器学习中的MLE、MAP、贝叶斯估计

原文地址：https://zhuanlan.zhihu.com/p/72370235

好文必须共享，感谢贪心科技的李文哲老师。讲得非常透彻。

以下是我的学习笔记

MLE(极大似然估计)、MAP(最大后验估计)以及贝叶斯估计(Bayesian)   三者的关系是什么呢？

一个具体的例子

"张三想从清华计算机系找一个优秀的学生帮忙分析一个数学难题，那张三用什么样的策略去寻求帮助呢？"

第一种策略 : MLE(极大似然估计)

从系里选出过往成绩最好的学生。比如我们可以选择过去三次考试中成绩最优秀的学生。

 

第二种策略：MAP(最大后验估计)

第二种策略中我们听取了老师的建议。根据考试成绩，前三名是小明、小花、小强。这时老师给出了自己的观点：“小明和小花的成绩中可能存在一些水分”。我们最后选择了小强。

与上一个策略唯一的区别在于这里多出了老师的评价，我们称之为 Prior。 也就是说我们根据学生以往的成绩并结合老师评价，选择了一位我们认为最优秀的学生（可以看成是模型）。之后就可以让他去回答张老师的难题 x'，并得到他的解答 y'。整个过程类似于MAP的估计以及预测。

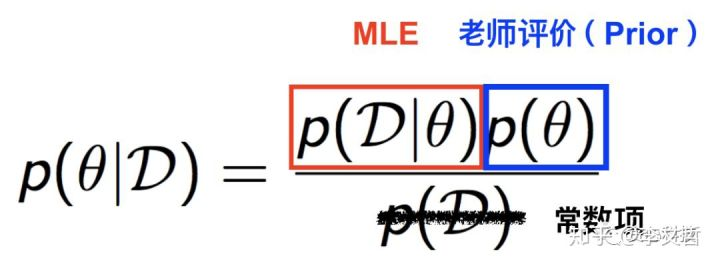
到这里，有些读者可能会有一些疑惑：“老师的评价(Prior)跟学生过往的成绩（Observation）是怎么结合在一起的？”。 为了回答这个问题，我们不得不引出一个非常著名的定理，叫做贝叶斯定理，如下图所示。左边的项是MAP需要优化的部分，通过贝叶斯定理这个项可以分解成MLE（第一种策略）和Prior，也就是老师的评价。在这里，分母是常数项（Constant），所以不用考虑。

 

 

 

第三种策略 - Bayesian

就是让所有人都去参与回答张三的难题，但最后我们通过一些加权平均的方式获得最终的答案。比如有三个学生，而且我们对这三个学生情况没有任何了解。通过提问，第一个学生回答的答案是A，第二个学生回答的答案也是A，但第三个学生回答的是B。在这种情况下，我们基本可以把A作为标准答案。接着再考虑一个稍微复杂的情况，假设我们通过以往他们的表现得知第三个学生曾经多次获得过全国奥赛的金牌，那这个时候该怎么办？ 很显然，在这种情况下，我们给予第三个学生的话语权肯定要高于其他两位学生。

每一位学生的话语权（权重）怎么得到呢？ 这就是贝叶斯估计做的事情！

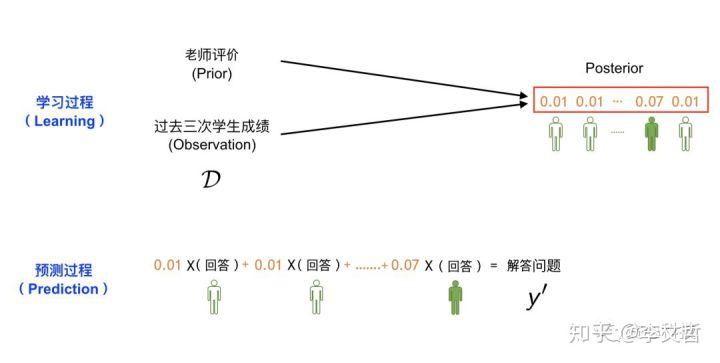
我们用下面的一幅图来讲述贝叶斯估计和预测的整个过程。跟MAP类似，我们已知每一位学生过去三次考试考试成绩（D）以及老师的评价（Prior）。 但跟MAP不同的是，我们这里的目标不再是- “选出最优秀的学生”，而是通过观测数据（D）去获得每一位学生的发言权（权重），而且这些权重全部加起来要等于1， 相当于是一个valid分布(distribution)。

总结起来，在第三种策略之下，给定过去考试成绩(D)和老师的评价（Prior）, 我们的目标是估计学生权重的分布，也称之为Posterior Distribution。 那这个分布具体怎么去估计呢？ 这部分就是贝叶斯估计做的事情，有很多种方法可以做这件事情，比如MCMC, Variational Method等等，但这并不是本文章的重点，所以不在这里进一步解释，有兴趣的读者可以关注之后关于贝叶斯的专栏文章。从直观的角度思考，因为我们知道每一位学生过往的成绩，所以我们很容易了解到他们的能力水平进而估计出每一位学生的话语权（权重）。

一旦我们获得了这个分布（也就是每一位学生的权重），接下来就可以通过类似于加权平均的方式做预测了，那些权重高的学生话语权自然就越大。

 

 

 

以上是对MLE, MAP以及贝叶斯估计的基本讲解。下面我们试图去回答两个常见的问题。

Q: 随着我们观测到越来越多的数据，MAP估计逐步逼近MLE，这句话怎么理解？

数据越多越准确啊，后验的不一定准啊。最大似然当然好了。

 

Q: 为什么贝叶斯估计会比MLE, MAP难？

回顾一下，MLE 和MAP都是在寻找一个最优秀的学生。贝叶斯估计则是在估计每一位学生的权重。第一种情况下，为了寻找最优秀的学生，我们只需知道学生之间的“相对”优秀程度。这个怎么理解呢？ 比如一个班里有三个学生A,B,C，我们知道学生A比B优秀，同时知道B比C优秀，那这时候就可以推断出学生A是最优秀的，我们并不需要明确知道A的成绩是多少，B的成绩是多少.....

但在贝叶斯估计模式下，我们必须要知道每一个学生的绝对权重，因为最后我们获得的答案是所有学生给出的答案的加权平均，而且所有学生的权重加起来要保证等于1(任何一个分布的积分和必须要等于1）。 假设我们知道每一位学生的能力值，a1, a2,.... an，这个能作为权重吗？ 显然不能。为了获得权重，有一种最简单的方法就是先求和，然后再求权重。比如先计算 a1+...+an = S, 再用a1/S 作为权重。这貌似看起来也不难啊，只不过多做了一个加法操作？

我们很容易看出这个加法操作的时间复杂度是O(n)，依赖于总体学生的数量。如果我们的假设空间只有几百名学生，这个是不成问题的。 但实际中，比如我们假设我们的模型用的是支持向量机，然后把假设空间里的每一个可行解比喻成学生，那这个假设空间里有多少个学生呢？ 是无数个！！， 也就是说需要对无穷多个数做这种加法操作。 当然，这种加法操作会以积分(integeral)的方式存在，但问题是这种积分通常没有一个closed-form的解，你必须要去近似地估计才可以，这就是MCMC或者Variational方法做的事情，不在这里多做解释。

 重点总结：

• 每一个模型定义了一个假设空间，一般假设空间都包含无穷的可行解；
• MLE不考虑先验（prior)，MAP和贝叶斯估计则考虑先验（prior）；
• MLE、MAP是选择相对最好的一个模型（point estimation）， 贝叶斯方法则是通过观测数据来估计后验分布(posterior distribution)，并通过后验分布做群体决策，所以后者的目标并不是在去选择某一个最好的模型；
• 当样本个数无穷多的时候，MAP理论上会逼近MLE；
• 贝叶斯估计复杂度大，通常用MCMC等近似算法来近似