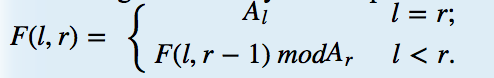「ACM Dalian Online 2016」H.Function（二分+RMQ）

---

描述

传送门：我是传送门

The shorter, the simpler. With this problem, you should be convinced of this truth.

You are given an array A of N postive integers, and M queries in the form (l,r). A function F(l,r) (1≤l≤r≤N) is defined as:

You job is to calculate F(l,r), for each query (l,r).

输入

There are multiple test cases.

The first line of input contains a integer TT, indicating number of test cases, and TTtest cases follow. 

For each test case, the first line contains an integer N(1≤N≤100000)N(1≤N≤100000).
The second line contains NN space-separated positive integers: A1,…,ANA1,…,AN (0≤Ai≤109)(0≤Ai≤109).
The third line contains an integer MM denoting the number of queries.
The following MM lines each contain two integers l,r(1≤l≤r≤N)l,r(1≤l≤r≤N), representing a query.

输出

For each query(l,r)(l,r), output F(l,r)F(l,r) on one line.

样例

输入

1
3
2 3 3
1
1 3

输出

2

思路

一个数比它大的数没有意义，比如10%100、20%30···

每次二分的找到右侧第一个比他小的就好了

代码

/*
 * =================================================================
 *
 *       Filename:  hdu5875.cpp
 *
 *           Link:  http://acm.hdu.edu.cn/showproblem.php?pid=5875
 *
 *        Version:  1.0
 *        Created:  2018/10/09 10时30分42秒
 *       Revision:  none
 *       Compiler:  g++
 *
 *         Author:  杜宁元 (https://duny31030.top/), duny31030@126.com
 *   Organization:  QLU_浪在ACM
 *
 * =================================================================
 */
#include <bits/stdc++.h>
using namespace std;
#define clr(a, x) memset(a, x, sizeof(a))
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define pre(i,a,n) for(int i=n;i>=a;i--)
#define ll long long
#define max3(a,b,c) fmax(a,fmax(b,c))
#define ios ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const int N = 100050;
int n,q,t,a,x,y;
vector<int> Q;
int dp_min[N][30];
void RMQ_init(const vector<int>& A)
{
    for(int i = 0;i < n;i++)
    {
        dp_min[i][0] = A[i];
    }
    for(int j = 1;(1 << j) <= n;j++)
        for(int i = 0;i + (1 << j) - 1 < n;i++)
        {
            dp_min[i][j] = min(dp_min[i][j-1],dp_min[i+(1 << (j-1))][j-1]);
        }
}

int RMQ_min(int L,int R)
{
    int k = 0;
    while((1 << (k+1)) <= (R-L+1))   // 如果2^(k+1) <= R-L+1,那么k还可以加1
    {
        k++;
    }
    // cout << "min = " << min(dp_min[L][k],dp_min[R-(1 << k)+1][k]) << endl;
    return min(dp_min[L][k],dp_min[R-(1 << k)+1][k]);
}


int main()
{
    ios
#ifdef ONLINE_JUDGE
#else
        freopen("in.txt","r",stdin);
    // freopen("out.txt","w",stdout);
#endif
    scanf("%d",&t);
    while(t--)
    {
        Q.clear();
        clr(dp_min,0);
        scanf("%d",&n);
        rep(i,1,n)  {   scanf("%d",&a); Q.push_back(a); }
        RMQ_init(Q);
        scanf("%d",&q);
        rep(i,1,q)
        {
            scanf("%d %d",&x,&y);
            x--,y--;
            int tmp = Q[x];
            if(x == y)
            {
                printf("%d\n",Q[x]);
                continue;
            }
            x++;
            while(x <= y)
            {
                int L= x,R = y;
                int flag = 0;
                while(L < R)
                {
                    int mid = (L+R) >> 1;
                    if(RMQ_min(L,mid) <= tmp)
                        R = mid;
                    else
                        if(RMQ_min(mid+1,R) <= tmp)
                            L = mid+1;
                        else
                        {
                            flag = 1;
                            break;
                        }
                }
                if(flag)    break;
                tmp %= Q[L];
                x = L+1;
            }
            printf("%d\n",tmp);
        }
    }
    fclose(stdin);
    // fclose(stdout);
    return 0;
}