网络流24题之方格取数问题 二分图+最小割
题目大意
在一个有\(n\times m\)个方格的棋盘中,每个方格中有一个正整数。现要从方格中取数,使任意\(2\)个数所在方格没有公共边,且取出的数的总和最大。试设计一个满足要求的取数算法。对于给定的方格棋盘,按照取数要求编程找出总和最大的数。
来看看怎么建图:
首先我们把棋盘红蓝二染色:

然后我们可以把它建成一张二分图(点上的数为在原图中的编号),附加一个超源和超汇,从超源向蓝点连一条容量为蓝点所代表的数的边,从红点向超汇连一条容量为红点所代表的数的边,然后从蓝点向与它相邻的红点连容量为\(INF\)的边:
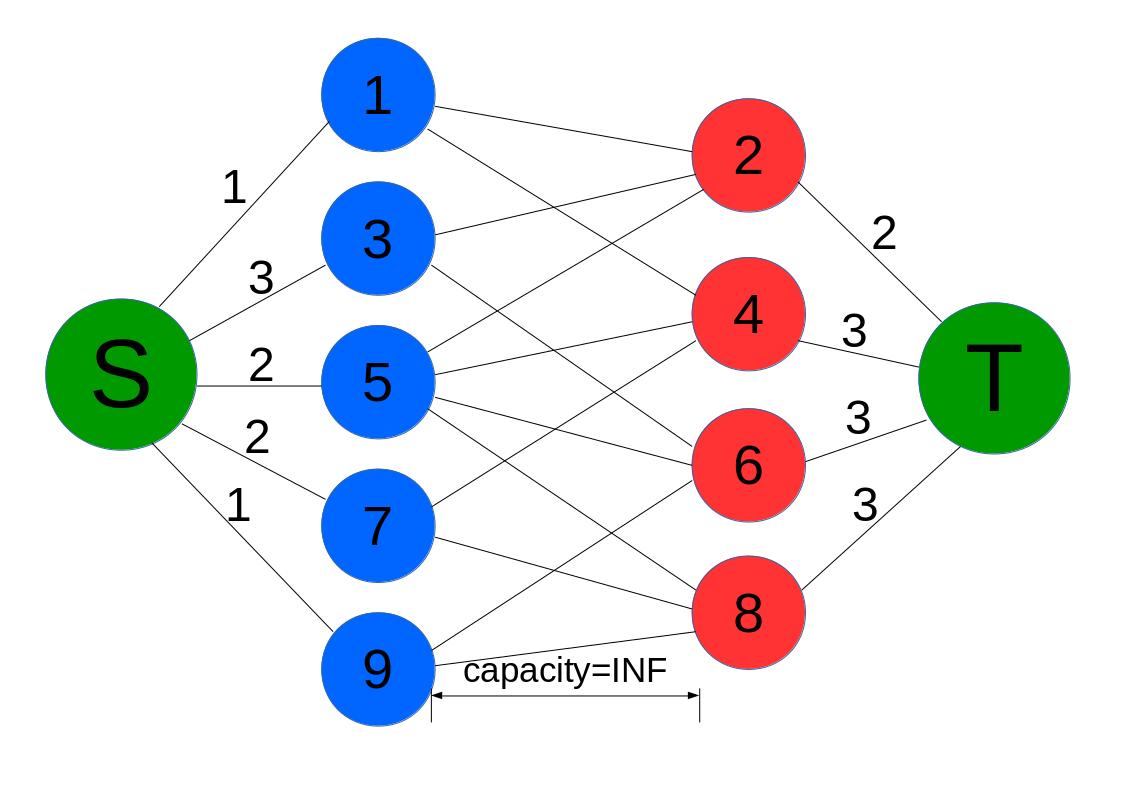
最后答案就是所有数的和减去最小割。
怎么理解这个建图呢?首先在最小割中中间的那些容量为\(INF\)的边一定没被割掉,其次最小割之后整张图就不连通了,假设我选了一个蓝点,那么它一定与\(T\)不连通,也就是与它相邻的红点的右侧那些边已经被割掉了,保证了答案的正确性。
代码排出来:
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
struct Edge
{
int to, cap, flow;
};
int n, m, S, T, sum, vis[10005], d[10005], cur[10005], w[105][105];
int dir[4][2] = {-1,0,1,0,0,-1,0,1};
vector<int> G[10005];
vector<Edge> edges;
void addEdge(int from, int to, int cap)
{
edges.push_back(Edge{to, cap, 0}), edges.push_back(Edge{from, 0, 0});
G[from].push_back(edges.size()-2), G[to].push_back(edges.size()-1);
}
int dfs(int u, int a)
{
if(u == T || !a) return a;
int flow = 0, f;
for(int &i = cur[u]; i < G[u].size(); ++i)
{
Edge &e = edges[G[u][i]];
if(d[e.to] == d[u]+1 && (f = dfs(e.to, min(a, e.cap-e.flow))) > 0)
{
e.flow += f, edges[G[u][i]^1].flow -= f;
flow += f, a -= f;
if(!a) break;
}
}
return flow;
}
int bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0;
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = 0; i < G[u].size(); ++i)
{
Edge e = edges[G[u][i]];
if(d[e.to] == -1 && e.cap > e.flow) d[e.to] = d[u]+1, q.push(e.to);
}
}
return ~d[T];
}
int maxFlow()
{
int flow = 0;
while(bfs()) memset(cur, 0, sizeof cur), flow += dfs(S, INF);
return flow;
}
int idx(int i, int j)
{
return (i-1)*m+j;
}
int main()
{
scanf("%d%d", &n, &m);
S = 0, T = n*m+1;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
{
scanf("%d", &w[i][j]);
sum += w[i][j];
}
for(int t = 2; t <= n+m; t += 2)
for(int x = 1, y; x <= t-1; ++x)
{
y = t-x;
if(x < 1 || x > n || y < 1 || y > m) continue;
addEdge(S, idx(x, y), w[x][y]);
for(int i = 0, tx, ty; i < 4; ++i)
{
tx = x+dir[i][0], ty = y+dir[i][1];
if(tx < 1 || tx > n || ty < 1 || ty > m) continue;
addEdge(idx(x, y), idx(tx, ty), INF);
if(!vis[idx(tx, ty)]) vis[idx(tx, ty)] = 1, addEdge(idx(tx, ty), T, w[tx][ty]);
}
}
printf("%d\n", sum-maxFlow());
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号