normalization, standardization and regularization

Normalization

Normalization refers to rescaling real valued numeric attributes into the range 0 and 1. It is useful to scale the input attributes for a model that relies on the magnitude of values, such as distance measures used in k-nearest neighbors and in the preparation of coefficients in regression.

normalization 是将数据的每个样本（向量）变换为单位范数的向量，各样本之间是相互独立的．其实际上，是对向量中的每个分量值除以正规化因子．常用的正规化因子有 L1, L2 和 Max．假设，对长度为 n 的向量，其正规化因子 z 的计算公式，如下所示：

注意：Max 与无穷范数  不同，无穷范数 是需要先对向量的所有分量取绝对值，然后取其中的最大值；而 Max 是向量中的最大分量值，不需要取绝对值的操作．

补充：一阶范数也称为曼哈顿距离（Manhanttan distance）或街区距离；二阶范数也称为欧式距离（Euclidean distance）

#!/usr/bin/env python
# -*- coding: utf8 -*-
# author: klchang
# Use sklearn.preprocessing.Normalizer class to normalize data.
from __future__ import print_function
import numpy as np
from sklearn.preprocessing import Normalizer


x = np.array([1, 2, 3, 4], dtype='float32').reshape(1,-1)

print("Before normalization: ", x)

options = ['l1', 'l2', 'max']
for opt in options:
    norm_x = Normalizer(norm=opt).fit_transform(x)
    print("After %s normalization: " % opt.capitalize(), norm_x)

#!/usr/bin/env python
# -*- coding: utf8 -*-
# author: klchang
# Use sklearn.preprocessing.normalize function to normalize data.

from __future__ import print_function
import numpy as np
from sklearn.preprocessing import normalize


x = np.array([1, 2, 3, 4], dtype='float32').reshape(1,-1)

print("Before normalization: ", x)

options = ['l1', 'l2', 'max']
for opt in options:
    norm_x = normalize(x, norm=opt)
    print("After %s normalization: " % opt.capitalize(), norm_x)

 

---

Standardizaton

Standardization refers to shifting the distribution of each attribute to have a mean of zero and a standard deviation of one (unit variance). It is useful to standardize attributes for a model that relies on the distribution of attributes such as Gaussian processes.

# Standardize the data attributes for the Iris dataset.
from sklearn.datasets import load_iris
from sklearn import preprocessing
# load the Iris dataset
iris = load_iris()
print(iris.data.shape)
# separate the data and target attributes
X = iris.data
y = iris.target
# standardize the data attributes
standardized_X = preprocessing.scale(X)

 

---

from 机器学习里的黑色艺术：normalization, standardization, regularization;

第一部分：大的层面上讲

1. normalization一般是把数据限定在需要的范围，比如一般都是【0，1】，从而消除了数据量纲对建模的影响。standardization 一般是指将数据正态化，使平均值0方差为1. 因此normalization和standardization 是针对数据而言的，消除一些数值差异带来的特种重要性偏见。经过归一化的数据，能加快训练速度，促进算法的收敛。

2.而regularization是在cost function里面加惩罚项，增加建模的模糊性，从而把捕捉到的趋势从局部细微趋势，调整到整体大概趋势。虽然一定程度上的放宽了建模要求，但是能有效防止over-fitting的问题(如图，来源于网上)，增加模型准确性。因此，regularization是针对模型而言。

 

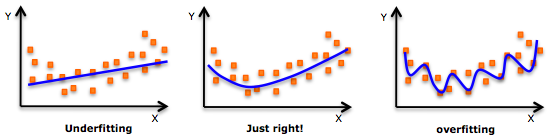
这三个term说的是不同的事情。

第二部分：方法

总结下normalization， standardization，和regularization的方法。

Normalization 和 Standardization

(1).最大最小值normalization： x'=(x-min)/(max-min). 这种方法的本质还是线性变换，简单直接。缺点就是新数据的加入，可能会因数值范围的扩大需要重新regularization。

(2). 对数归一化：x'=log10(x)/log10(xmax)或者log10(x)。推荐第一种，除以最大值，这样使数据落到【0，1】区间

(3).反正切归一化。x'=2atan(x)/pi。能把数据投影到【-1，1】区间。

(4).zero mean normalization归一化，也是standardization. x'=(x-mean)/std.

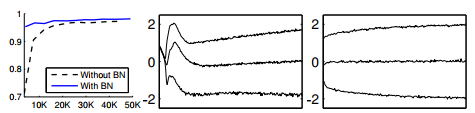
有无normalization，模型的学习曲线是不一样的，甚至会收敛结果不一样。比如在深度学习中，batch normalization有无，学习曲线对比是这样的：图一 蓝色线有batch normalization （BN）,黑色虚线是没有BN. 黑色线放大，是图二的样子，蓝色线放大是图三的样子。reference:Batch Normalization: Accelerating Deep Network Training by Reducing
Internal Covariate Shift， Sergey Ioffe.

Regularization 方法

一般形式，应该是 min  , R是regularization term。一般方法有

1. L1 regularization: 对整个绝对值只和进行惩罚。
2. L2 regularization：对系数平方和进行惩罚。
3. Elastic-net 混合regularization。

 

---

from Differences between normalization, standardization and regularization;

Normalization

Normalization usually rescales features to $[0,1]$.¹ That is,

$$x^{\prime }=\frac{x-min\left(x\right)}{max\left(x\right)-min\left(x\right)}$$

It will be useful when we are sure enough that there are no anomalies (i.e. outliers) with extremely large or small values. For example, in a recommender system, the ratings made by users are limited to a small finite set like $\{1,2,3,4,5\}$.

In some situations, we may prefer to map data to a range like $[-1,1]$ with zero-mean.² Then we should choose mean normalization.³

$$x^{\prime }=\frac{x-mean\left(x\right)}{max\left(x\right)-min\left(x\right)}$$

In this way, it will be more convenient for us to use other techniques like matrix factorization.

Standardization

Standardization is widely used as a preprocessing step in many learning algorithms to rescale the features to zero-mean and unit-variance.³

$$x^{\prime }=\frac{x-\mu }{\sigma }$$

Regularization

Different from the feature scaling techniques mentioned above, regularization is intended to solve the overfitting problem. By adding an extra part增加惩罚项 to the loss function, the parameters in learning algorithms are more likely to converge to smaller values, which can significantly reduce overfitting.

There are mainly two basic types of regularization: L1-norm (lasso) and L2-norm (ridge regression).⁴

L1-norm⁵

The original loss function is denoted by $f\left(x\right)$, and the new one is $F\left(x\right)$.

$$F\left(x\right)=f\left(x\right)+\lambda {\parallel x\parallel }_1$$

where

$${\parallel x\parallel }_p=\sqrt[p]{p\sum _{i=1}^n{\left|x_i\right|}^p}$$

L1 regularization is better when we want to train a sparse model, since the absolute value function is not differentiable at 0.

L2-norm⁵⁶

$$F\left(x\right)=f\left(x\right)+\lambda {\parallel x\parallel }_2^2$$

L2 regularization is preferred in ill-posed problems for smoothing.

Here is a comparison between L1 and L2 regularizations.

 

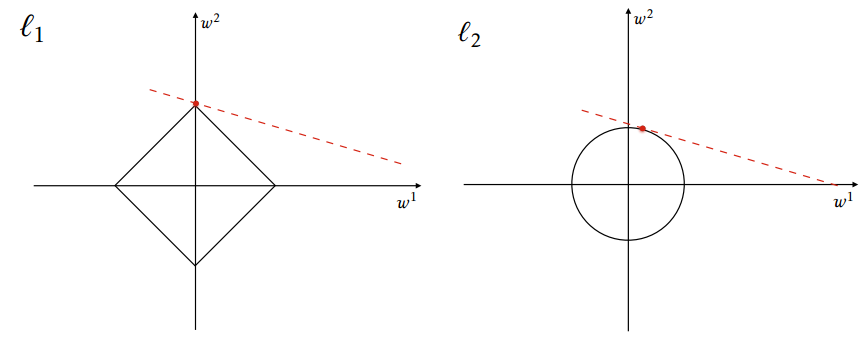
From https://en.wikipedia.org/wiki/Regularization_(mathematics)

References

1. https://stats.stackexchange.com/a/10298 ↩

2. https://www.quora.com/What-is-the-difference-between-normalization-standardization-and-regularization-for-data/answer/Enzo-Tagliazucchi?share=c48b6752&srid=51VPj ↩

3. https://en.wikipedia.org/wiki/Feature_scaling ↩ ↩²

4. https://en.wikipedia.org/wiki/Regularization_%28mathematics%29 ↩

5. https://www.quora.com/What-is-the-difference-between-L1-and-L2-regularization-How-does-it-solve-the-problem-of-overfitting-Which-regularizer-to-use-and-when/answer/Kenneth-Tran?share=400c336d&srid=51VPj ↩ ↩²

6. https://en.wikipedia.org/wiki/Ridge_regression ↩