《深入理解计算机系统》CSAPP_DataLab
Data Lab
Link:CS:APP3e(该链接被限制访问)
也可自行在github中搜索csapplab,以找到实验原文件。
操作系统:linux
Memory Dot 我的个人博客,欢迎来玩。
one
bitXor
- bitXor - x^y using only ~ and &
- Example: bitXor(4, 5) = 1
- Legal ops: ~ &
- Max ops: 14
- Rating: 1
bitXor:实现位级异或,限制操作: ~ &
int bitXor(int x, int y) {
return ~((~(x&~y)) & (~(~x&y)));
//XOR的与或非实现、OR的与非实现,两者组合,达成xor的与非实现
}
思路:
XOR的与或非实现: (x & ~ y)|( ~ x & y); OR的与非实现: ~ (~ a & ~ b)
time
- tmin - return minimum two's complement integer
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 4
- Rating: 1
tmin:位级实现输出Tmin
一开始没认真看INTEGER CODING RULES的要求,后来才发现,仅允许使用0 ~ 255之间的数值,-1 << 31 虽然是对的,但不符合要求
int tmin(void) {
return 1 << 31; //0x80000000
}
two
isTmax
- isTmax - returns 1 if x is the maximum, two's complement number,
- and 0 otherwise
- Legal ops: ! ~ & ^ | +
- Max ops: 10
- Rating: 1
isTmax:判断输入的数值是否为Tmax即0x7FFFFFFF,是,输出1,否则,输出0
不知道为啥上面题目是tmin,这里就是Tmax,为啥大小写不统一呢?绝对是出题老师偷懒了。
int isTmax(int x) {
return !((x^~(x+1))|(!(~x))); //或者!(x^~(x+1)) & !(!(x+1));
}
思路:
由于Tmax == ~(Tmax+1),|左边利用异或^充当判断==,相等其值为0, |右边排除-1即0xffffffff (因为-1 == ~(-1+1));tmax按位取反再按数值取反后,为0, -1按位取反再按数值取反后,为1
allOddBits
- allOddBits - return 1 if all odd-numbered bits in word set to 1
- where bits are numbered from 0 (least significant) to 31 (most significant)
- Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
- Legal ops: ! ~ & ^ | + << >>T
- Max ops: 12
- Rating: 2
allOddBits:判断一个数的奇数位(odd)是否全为1,是,输出1,否则,输出0
int allOddBits(int x) {
int mask = 0xaa | 0xaa << 8;
mask = mask | mask << 16;
x = x & mask;
return !(x^mask);
}
思路:
先构造0xAAAAAAAA,利用 <<、|即可,再用x XOR x的必为0的性质,逻辑取反即可
negate
- negate - return -x
- Example: negate(1) = -1.
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 5
- Rating: 2
negate:取相反数
不知道的时候是真的不知道= =
int negate(int x) {
return (~x)+1; //按位取反,再加1即可
}
three
isAsciiDigit
- isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
- Example:
- isAsciiDigit(0x35) = 1.
- isAsciiDigit(0x3a) = 0.
- isAsciiDigit(0x05) = 0.
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 15
- Rating: 3
isAsciiDigit:判断一个数是否在0x30 <= x <= 0x39之间,是,输出1,否则,输出0
自己的思路把前半部的信息给清除了,不能用。还是大佬强,还具有扩展性,改变上下限数值就是改变范围了。
int isAsciiDigit(int x) {
int sign = 1<<31;
return !(((sign&((~(sign|0x39))+x))>>31) | ((sign&(~0x30+1+x))>>31));
}
思路:
上限(左边),目的是使输入的数大于0x39时,真值为1;下限(右边),目的是使输入的数小于0x30时,真值为1,
当两边的真值为0时,才居于范围之间,输出1
先取一个符号位sign即0x80000000
左边:
0x39按位或sign后再取反,目的是得到一个低8位为0xc6,符号位为0,其它位为1的位级。
该位级+x后,若x大于0x39则其符号位变为1,反之为0
&sign取符号位后,再右移31。若其值大于0x39则为-1,反之为0。
右边:
0x30按位取反+1,目的是得到一个低8位为0xd0,符号位为1,其它位为1的位级。
该位级加x后,若x小于0x30则其符号位仍为1,反之为0
&sign取符号位后,再右移31。若其值小于0x30为-1,反之为0。
conditional
- conditional - same as x ? y : z
- Example: conditional(2,4,5) = 4
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 16
- Rating: 3
conditional:用位级运算实现三目运算符(x ? y : z)
思路往往可以更简洁
//法一
int conditional(int x, int y, int z) {
x = (!!x)<<31>>31;//use: overturn( logic); by <<31>>31
return (x&y)|(~x&z);
}
思路:
用x构造出全1或全0,再使全1、全0分别与x、y对应。
x逻辑取反两次得真值,再<<31>>31,使真值1变为全1即-1,真值0不变
此时,若x为-1,则&y得到y,且按位取反x,并&z清空;若x为0,则&y清空,且按位取反x,并&z得到z
而后按位或输出
//法二
int conditional(int x, int y, int z) {
x = !!x;
x = ~x+1;//use: overturn(bits, logic); by -1+1 = 0;0xfffffffe+1 = 0xffffffff = -1
return (x&y)|(~x&z);
}
思路:
同法一类似,只是构造全1或者全0的方法不同
用x构造出全1或全0,再使全1、全0分别与x、y对应。
x逻辑取反两次得真值,再按位取反后+1,使真值1变为全1即-1,真值0不变
此时,若x为-1,则&y得到y,且按位取反x,并&z清空;若x为0,则&y清空,且按位取反x,并&z得到z
而后按位或输出
//法三
int conditional(int x, int y, int z) {
int neg_1 = ~0
return ((!x)+neg_1)&y | ((!!x)+neg_1)&z;
}
思路:
x不为0时,输出y;x为0时,输出z。想办法使两者分别对应,利用非!翻转(x不为0翻转1次得全0 or x为0翻转2次得全0)使两者分别对应
再用-1(neg_1)配出我们要的全1,以便&x或y()。
运算过程:
左边:若x不为0,则翻转一次后-1,为全1,可得y值;若x为0,则翻转再-1,为全0,可清空y值;
右边:若x不为0,则翻转两次后-1,为全0,可清空z值;若x为0,则两次翻转再-1,为全1,可得到z值;
两边取或,可输出数字(return竟然可以输出数值!!哭笑)
isLessOrEqual
- isLessOrEqual - if x <= y then return 1, else return 0
- Example: isLessOrEqual(4,5) = 1
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 24
- Rating: 3
isLessOrEqual:判断是否x <= y,是,输出1,否则,输出0
一般自己写的都有点长
int isLessOrEqual(int x, int y) {
return !!(!(x^y) ^ ((x>>31)^(y>>31)&(x>>31)) ^ !((x>>31)^(y>>31))&(x+((~y)+1))>>31); // if not use !!() will return -1
}
思路:
判断x<=y,分成三段解决,任意情况成立即可,则用XOR连接,1.两者相等;两者不相等时,2.sign不同;3.sign相同。
1.XOR清零再逻辑非即可
2.先限定于sign不同的情况,利用XOR
再&(x>>31),保留x的sign位,若sign=1,x为负数,则全1输出;若sign=0,x为正数,则全0输出
3.先限定于sign相同的情况(即排除sign不同的情况),再利用作差,x-y,小于0时,符合题意,且sign位为1,最后>>31,分割出全0和全1
XOR连接完后,为满足符合return 1, 否则return 0,要取两次逻辑非
logicalNeg
- logicalNeg - implement the ! operator, using all of
- the legal operators except !
- Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
- Legal ops: ~ & ^ | + << >>
- Max ops: 12
- Rating: 4
logicalNeg:实现逻辑非,限制操作:~ & ^ | + << >>
//法一
int logicalNeg(int x) {
int sign = 1<<31;
int all1 = ~0;
return ((((~x)|sign)+1)>>31)+1 & (x^sign)>>31 ; //((x^sign)>>31)
}
思路:
实现逻辑非!,即实现0输出1,非0输出0。
首先要分割0和非0部分,办法是0将保持为0,非0全部转换为负数使其符号位为1。,
用 ~ x 翻转,~ 0 = -1,非0保持不变 ;
(~ x) | sign),使-1不变,非0数全部转换为负数且最大值为-2,但注意到x=sign经运算后也为-1,用&(x^sign)>>31剔除,同时,使x=0时,第0位为1;
((~ x) | sign)+1),使-1变0,负数最大值此时为-1;
((~ x) | sign)+1)>>31,0不变,负数全为-1;
((((~ x) | sign)+1)>>31)+1,0变1,-1全变为0;
((((~ x) | sign)+1)>>31)+1 & (x^sign)>>31,x=0时,(左边1 & 右边-1)输出1;x为非0数时,(左边0 &右边任何数)输出0;
法二:
int logicalNeg(int x) {
return ((x|(~x+1))>>31)+1;
}
思路:
利用补码(取反+1)的性质,0和Tmin的补码为本身,其它数值的补码为其相反数;
0与其补码按位或之后,其值为全0,Tmin与其补码、其它数值与其补码,按位或之后,符号位为1;
然后>>31,0不变,Tmin、其它数值为全1即-1;
而后+1,0变为1,Tmin、其它数值为0;
howManyBits
- howManyBits - return the minimum number of bits required to represent x in
- two's complement
- Examples:
- howManyBits(12) = 5
- howManyBits(298) = 10
- howManyBits(-5) = 4
- howManyBits(0) = 1
- howManyBits(-1) = 1
- howManyBits(0x80000000) = 32
- Legal ops: ! ~ & ^ | + << >>
- Max ops: 90
- Rating: 4
howManyBits:求一个数最少要用多少位表示
这道题想了很久,因为允许90个ops,就慢慢找规律,最终想出最高位和次最高位相异时,该数的位数可以确定,但实际只能从1位到32位一个个判断,总共操作接近300ops,只能翻起答案来= =,知道会用重复判断的方法,没想到是二分法这么巧妙
int howManyBits(int x) {
int b16,b8,b4,b2,b1,b0;
int sign = x>>31;
x = (sign&~x)|(~sign&x);//x为正数不变;x为负数按位取反,其符号位变为0,可将负数当作正数来求其所需最少的表达位数
// 二分法,不断缩小范围
b16 = !!(x>>16)<<4;//高十六位是否有1
x = x>>b16;//如果有(至少需要16位),则将原数右移16位
b8 = !!(x>>8)<<3;//剩余位高8位是否有1
x = x>>b8;//如果有(至少需要16+8=24位),则右移8位
b4 = !!(x>>4)<<2;//剩余位高4位是否有1
x = x>>b4;//如果有(至少需要16+8+4=28位),则右移4位
b2 = !!(x>>2)<<1;//剩余位高2位是否有1
x = x>>b2;//如果有(至少需要16+8+4+2=30位),则右移2位
b1 = !!(x>>1);//剩余位高1位是否有1
x = x>>b1;// 如果有(至少需要16+8+4+2+1=31位),则右移位
b0 = x;//b0为x,数值为1或者0
return b16+b8+b4+b2+b1+b0+1;//+1表示加上符号位
}
思路:
如果是一个正数,则需要找到它最高为1的是第几位(假设该位是第n位),再加上符号位0(计数为1),那么它最少需要n+1位来表示;
如果是一个负数,则需要找到它最高为0的是第几位(假设该位是第m位),那么它最少需要m位来表示
float
一开始是真的懵,想来是浮点数位级表示学得比较模糊
floatScale2
- floatScale2 - Return bit-level equivalent of expression 2*f for
- floating point argument f.
- Both the argument and result are passed as unsigned int's, but
- they are to be interpreted as the bit-level representation of
- single-precision floating point values.
- When argument is NaN, return argument
- Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
- Max ops: 30
- Rating: 4
floatScale2:用unsigned的位级来表示一个浮点数uf,同时,对浮点数uf乘2
unsigned floatScale2(unsigned uf) {
int exp = (uf&0x7f800000)>>23;//取指数exp
int sign = uf&0x80000000;//取符号位sign
if(exp==0) return uf<<1|sign;//输出(非规化数)*2或者0*2
if(exp==255) return uf;//输出NaN或者INF(无穷,包括正无穷和负无穷)
exp++; //计算(规化数)*2,
if(exp==255) return 0x7f800000|sign;//(规化数)*2后,若指数exp全为1即INF,则输出0x7f800000|sign
return (exp<<23)|(uf&0x807fffff);//(规化数)*2后,若指数exp不全为1就仍为规划数,则输出(exp<<23)|(uf&0x807fffff)
}
思路:
区分规化数、非规化数、NaN、INF,注意区分的时候,都要乘2
第5行,不用exp<<1的原因是:虽然能达到*2的目的,但可能会使exp越出255,突破exp限定的8位
floatFloat2Int
- floatFloat2Int - Return bit-level equivalent of expression (int) f
- for floating point argument f.
- Argument is passed as unsigned int, but
- it is to be interpreted as the bit-level representation of a
- single-precision floating point value.
- Anything out of range (including NaN and infinity) should return
- 0x80000000u.
- Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
- Max ops: 30
- Rating: 4
floatFloat2Int:用unsigned位级表示浮点数uf强制转换为int整型数
int floatFloat2Int(unsigned uf)
{
int sign = (uf >> 31) & 1;//取符号位sign
int bias = 127;//偏置值为(2 ^ (8-1)) - 1
int exp = (uf >> 23) & 0xFF;//取指数exp
int E = exp - bias; //指数exp的真实值,即阶码E
int frac = uf & 0x007FFFFF;//取小数字段frac,注意符号位被剔除了
int M = frac | 0x00800000; //将第23位置1,即阶码的最后1位置1,因为:规化数之中尾数M的范围是(1 ~ 2-ξ)
int tar;
if (sign) sign = -1;
else sign = 1;//符合位取(-1) ^ 0=1 或者 (-1) ^ 1=-1 ,用以保持正数,或者转为负数
if (E >= 31)
return 0x80000000;
if (E < 0)
return 0;
if (E >= 23)
tar = sign * (M << (E - 23));//E大于23时,则M左移(E - 23),同时考虑正负数
else if (E < 23)
tar = sign * (M >> (23 - E));//E小于23时,则M右移(23 - E),同时考虑正负数
return tar;
}
思路:
区分float型的规化数、非规化数、INF、NaN,
INF、NaN:其E >= 31 计算阶码值2^E,超出int型Tmax == 0x7fffffff,直接输出0x80000000
非规化数:其E < 0 计算阶码值2^E,为小数,直接输出0
规化数: 其31> E >=0 计算阶码值2^E,居于1 ~ 2^30之间,需要左右移
左右移原理见 CSAPP P82
其结论是:阶码E大于尾数位数(float型取frac字段位数,共23位)时,则M左移(23 - E)(最多移8位);阶码E小于尾数位数,则M右移(23 - E)(最多移23位)
原解法对于E=23时,直接输出tar=0;对于E=31时,将其看作仍可以做M左移运算,事实上2 ^ E = 2 ^ 31,已经超过int型Tmax = (2 ^ 31) - 1
但检测可以通过 纠正1:虽然超过了Tmax,但没有超过Tmin = - 2 ^ 31,故,对于E=31时,将其看作仍可以做M左移运算。纠正2:只要E取31时,左移时,必然移动8位到符号位且置1,因为:规化数的阶码E最后1位为1。那么,符号位为0,frac字段全0时,其值为2 ^ 31,左移8位后为0x80000000;符号位为0,frac字段非0时,其值超过2 ^ 31,要置为INF(0x80000000);符号位为1,frac字段全0时,其值为-2 ^ 31,左移8位后为0x80000000;符号位为1,frac字段非0时,其值为超过-2 ^ 31,要置为INF。综合下来,E = 31时,可以直接置为INF。
笔者做出修正
对于E=23时,输出tar = sign*M;对于E=31时,直接输出0x80000000(本题Anything out of range return 0x80000000)
floatPower2
- floatPower2 - Return bit-level equivalent of the expression 2.0^x
- (2.0 raised to the power x) for any 32-bit integer x.
- The unsigned value that is returned should have the identical bit
- representation as the single-precision floating-point number 2.0^x.
- If the result is too small to be represented as a denorm, return 0.
- If too large, return +INF.
- Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
- Max ops: 30
- Rating: 4
floatPower2:输入一个int x,用unsigned位级表示2.0 ^ x
unsigned floatPower2(int x) {
unsigned INF = 0xff << 23;
int exp = x + 127;
if(exp >= 255) return INF;
if(exp < -23) return 0;
if(exp <= 0) return 0x00400000>>(~exp+1);
return exp << 23;
}
思路:
首先需要定义INF,为exp全1即0xff << 23;其次定义小于2 ^(-126-23)为0
x的取值即为E,exp = E + bias,可计算出指数exp,而后
考虑临界值:
bin(x) = 0 00000000 00000000000000000000001,此数是2 ^ (-126-23),(最小值)
即exp = 0时情况;exp小于等于0,我们取 0x00400000>>( ~exp+1)
bin(x) = 0 00000001 00000000000000000000000,此数是2 ^ (-126),
即exp = 1时情况;exp居于0 ~ 254时,我们取exp << 23
bin(x) = 0 11111111 00000000000000000000000 ,此数是2 ^ (128),(大于最大值)
即exp = 255时情况。exp大于等于exp全1,我们取INF
以及,exp小于-23时,超出最小值,我们取0。
补充:
这里如果机子性能不强可能会超时,可以更改btest.c里的TIMEOUT_LIMIT,以避免超时出错
附图:
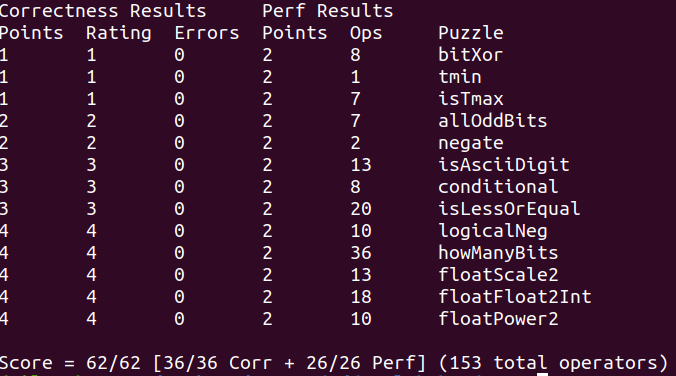
感想:
- 雄关漫道真如铁,而今迈步从头越
- 从9.4号开始做这个lab,一直到9.12号,一共9天。难度真是比较大,终于感受到很名校同学的差距了(特别是那道ASCII)。平时很少做这样的题。他们是把CSAPP当作ICS(计算机导论)来上的,我得向这些他们靠近。转专业并降级的我已经落后了不少,是时候好好学了。
- 现在看难度1、2觉得很容易,但一开始做的时候还是一头雾水的。位级运算的不但功能十分强大,而且还极大地减少运算时间。之后还得花点心思巩固。英文阅读能力非常需要提高,浮点题那一块,题目都看不太懂。以后做题前先翻翻书,想想知识点,不要直接凭空硬莽。
- 如有谬误,敬请指正。
- Memory Dot,我的个人博客,欢迎来玩。

 data lab 位级运算实验
data lab 位级运算实验

 浙公网安备 33010602011771号
浙公网安备 33010602011771号