Leetcode回溯法
回溯法简介
回溯法是复杂度很高的暴力搜索算法,实现简单且有固定模板,常被用于搜索排列组合问题的所有可行解。不同于普通的暴力搜索,回溯法会在每一步判断状态是否合法,而不是等到状态全部生成后再进行确认。当某一步状态非法时,它将回退到上一步中正确的位置,然后继续搜索。前进和后退是回溯法关键的动作。
回溯的本质就是暴力枚举所有可能。要注意的是,由于回溯通常结果集都记录在回溯树的路径上,因此如果不进行撤销操作, 则可能在回溯后状态不正确导致结果有差异, 因此需要在递归到底部往上冒泡的时候进行撤销状态。
如果你每次递归的过程都拷贝了一份数据,那么就不需要撤销状态,相对地空间复杂度会有所增加
算法流程
构造空间树。
进行遍历。
如遇到边界条件,即不再向下搜索,转而搜索另一条链。
达到目标条件,输出结果。
伪代码
const visited = {}
function dfs(i) {
if (满足特定条件){
// 返回结果 or 退出搜索空间
}
visited[i] = true // 将当前状态标为已搜索
dosomething(i) // 对i做一些操作
for (根据i能到达的下个状态j) {
if (!visited[j]) { // 如果状态j没有被搜索过
dfs(j)
}
}
undo(i) // 恢复i
}39 组合总和
题目描述
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
下述代码的解释:

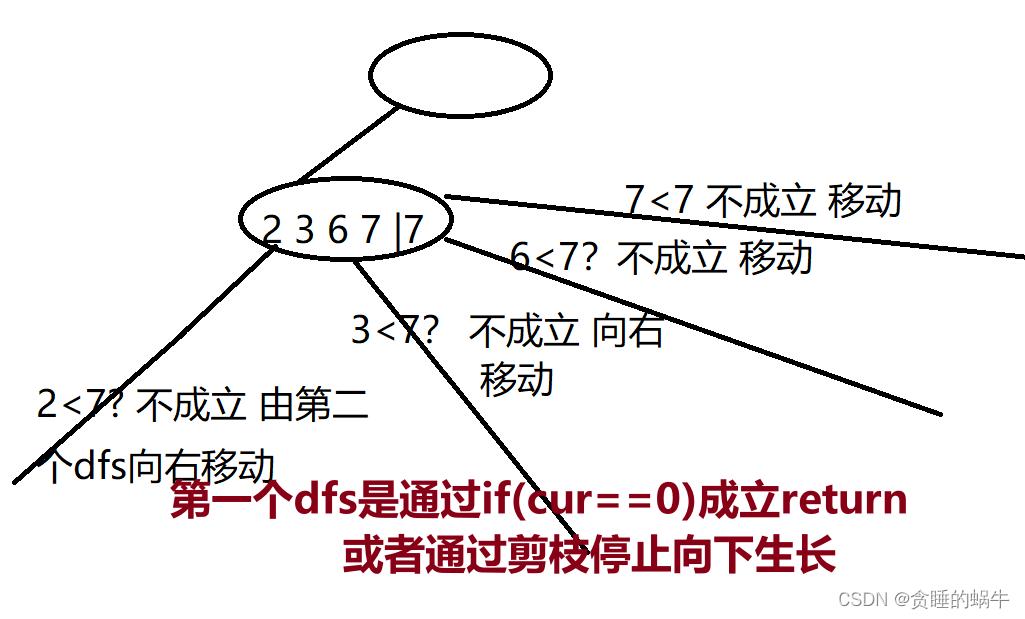
第二个dfs是通过超过数组个数则停止向右移动
不管是第一个dfs还是第二个dfs,两者生长都是在同一个节点上向下或者右下。

代码
import java.util.ArrayList;
import java.util.List;
public class L16 {
public static void main(String[] args) {
Solution solution=new Solution();
int[] candidates= {2,3,6,7};
solution.combinationSum(candidates,7);
System.out.println(solution.ans);
}
}
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
dfs(candidates, 0, target, new ArrayList<>());
return ans;
}
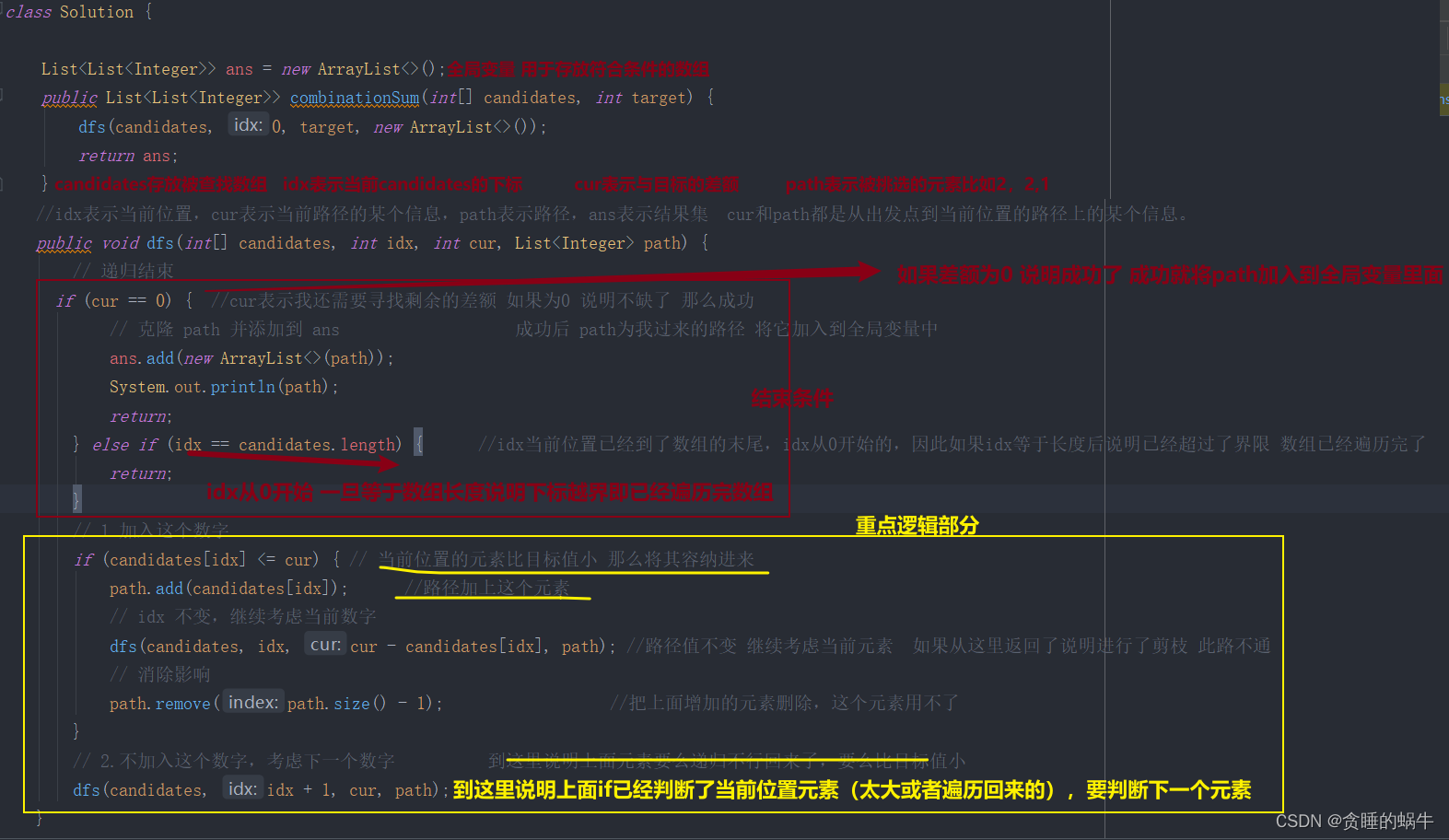
//idx表示当前位置,cur表示当前路径的某个信息,path表示路径,ans表示结果集 cur和path都是从出发点到当前位置的路径上的某个信息。
public void dfs(int[] candidates, int idx, int cur, List<Integer> path) {
// 递归结束
if (cur == 0) { //cur表示我还需要寻找剩余的差额 如果为0 说明不缺了 那么成功
// 克隆 path 并添加到 ans 成功后 path为我过来的路径 将它加入到全局变量中
ans.add(new ArrayList<>(path));
System.out.println(path);
return;
} else if (idx == candidates.length) { //idx当前位置已经到了数组的末尾,idx从0开始的,因此如果idx等于长度后说明已经超过了界限 数组已经遍历完了
return;
}
// 1.加入这个数字
if (candidates[idx] <= cur) { // 当前位置的元素比目标值小 那么将其容纳进来
path.add(candidates[idx]); //路径加上这个元素
// idx 不变,继续考虑当前数字
dfs(candidates, idx, cur - candidates[idx], path); //路径值不变 继续考虑当前元素 如果从这里返回了说明进行了剪枝 此路不通
// 消除影响
path.remove(path.size() - 1); //把上面增加的元素删除,这个元素用不了
}
// 2.不加入这个数字,考虑下一个数字 到这里说明上面元素要么递归不行回来了,要么比目标值小
dfs(candidates, idx + 1, cur, path);
}
}40 组合总数
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
思路
数组中每个数字只能使用一次
数组中可能存在数字
去除重复组合办法

class Solution {
List<List<Integer>> ans = new ArrayList<>();
Set<Integer> visited = new HashSet<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
dfs(candidates, 0, target);
return ans;
}
public void dfs(int[] candidates, int idx, int cur) {
if (cur == 0) {
ans.add(new ArrayList<>(path));
return;
} else if (idx == candidates.length) {
return;
}
// 当前数字与前面数字相同并且前面数字没有在路径中,则忽略这个数字
if (idx != 0 && candidates[idx] == candidates[idx - 1] && !visited.contains(idx - 1)) {
dfs(candidates, idx + 1, cur);
return;
}
// 1.加入这个数字
if (candidates[idx] <= cur) {
path.add(candidates[idx]);
visited.add(idx);
// 向下递归时考虑下一个数字
dfs(candidates, idx + 1, cur - candidates[idx]);
// 消除影响
path.remove(path.size() - 1);
visited.remove(idx);
}
// 2.不加入这个数字
dfs(candidates, idx + 1, cur);
}
}78 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例:
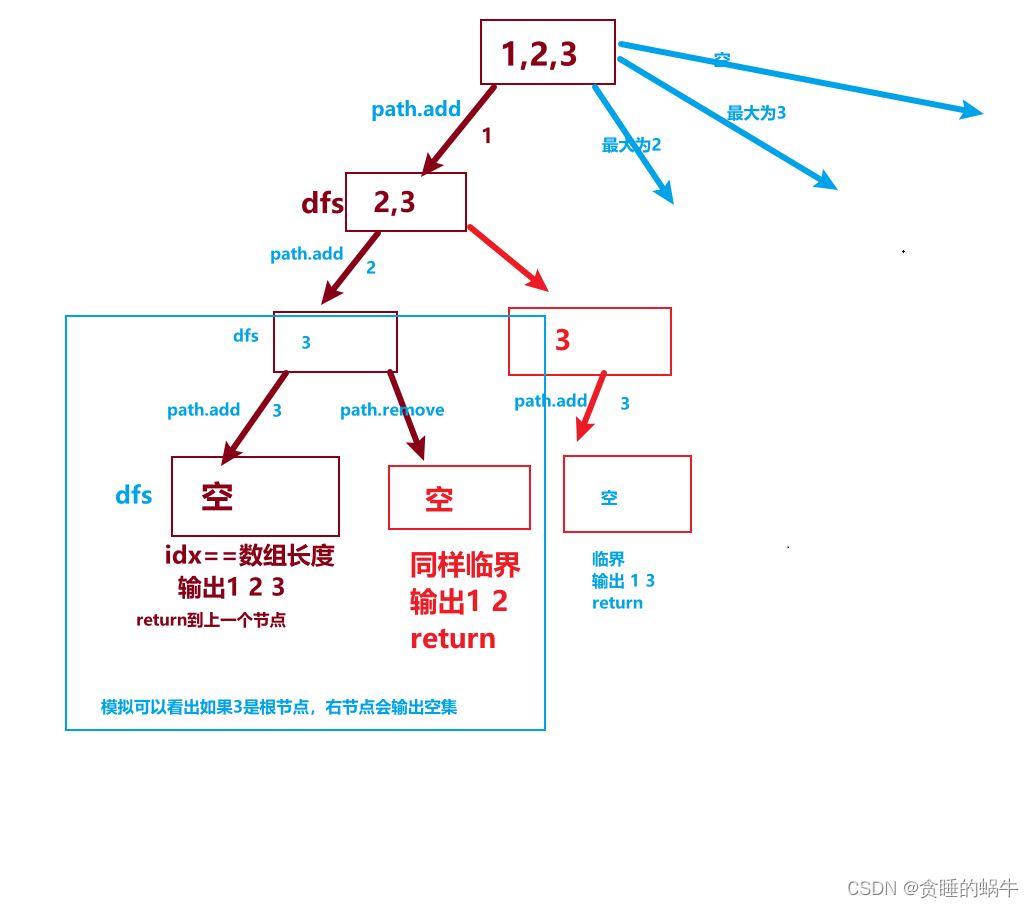
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

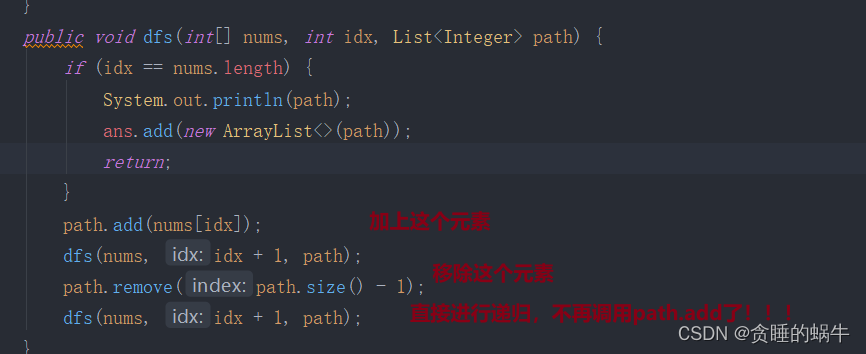
class Solution {
List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
dfs(nums, 0, new ArrayList<>());
return ans;
}
public void dfs(int[] nums, int idx, List<Integer> path) {
if (idx == nums.length) {
ans.add(new ArrayList<>(path));
return;
}
path.add(nums[idx]);
dfs(nums, idx + 1, path);
path.remove(path.size() - 1);
dfs(nums, idx + 1, path);
}
}
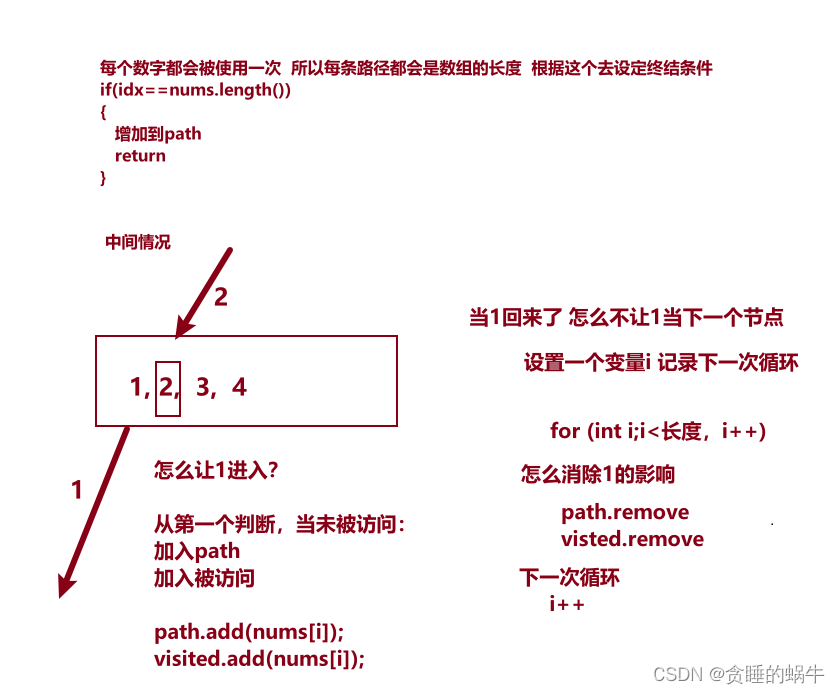
46 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class L16_4 {
public static void main(String[] args) {
Solution4 solution=new Solution4();
int[] candidates= {1,2,3};
solution.permute(candidates);
// System.out.println(solution.ans);
}
}
class Solution4 {
List<List<Integer>> ans = new ArrayList<>();
Set<Integer> visited = new HashSet<>();
// List<Integer> path = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
dfs(nums, 0, new ArrayList<>());
return ans;
}
public void dfs(int[] nums, int idx, List<Integer> path) {
int i=0;
if (idx == nums.length) {
System.out.println(path);
ans.add(new ArrayList<>(path));
return;
}
while(i<nums.length)
{
while(visited.contains(i)) i++;
if(i<nums.length) {
visited.add(i);
path.add(nums[i]);
dfs(nums, idx + 1, path);
visited.remove(i);
path.remove(path.size() - 1);
i++;
}
}
}
}增加代码简洁文章,本代码为第一个例子代码简洁化_贪睡的蜗牛的博客-CSDN博客
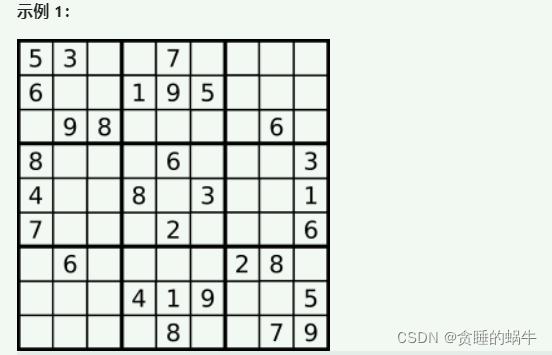
37 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。

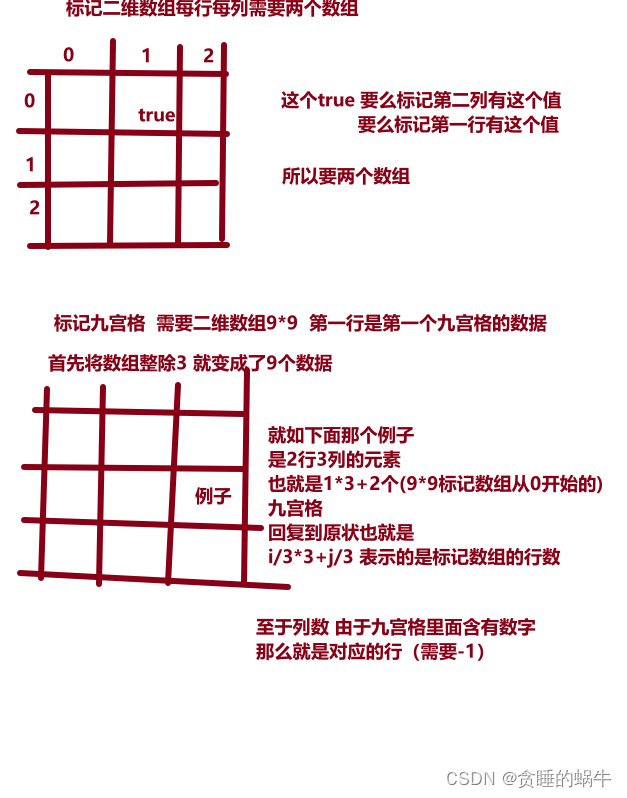
visted表示
关于思路,上面全排列是有不能重复的限制,这里有三个限制
下面代码有点问题,dfs是标准答案,dfs2是我想把所有答案打印出来,有问题。
public class L16_5 {
public static void main(String[] args) {
Solution5 solution=new Solution5();
int[] candidates= {2,3,6,7};
char [][]board = new char[][]{{'5','3','.','.','7','.','.','.','.'},{'6','.','.','1','9','5','.','.','.'},{'.','9','8','.','.','.','.','6','.'},{'8','.','.','.','6','.','.','.','3'},{'4','.','.','8','.','3','.','.','1'},{'7','.','.','.','2','.','.','.','6'},{'.','6','.','.','.','.','2','8','.'},{'.','.','.','4','1','9','.','.','5'},{'.','.','.','.','8','.','.','7','9'}};
// solution.dfs2();
// System.out.println((char)5);
solution.solveSudoku(board);
// for(int i=0;i<9;i++)
// {
// for (int j=0;j<9;j++)
// System.out.print(board[i][j]);
// System.out.println();
// }
}
}
class Solution5 {
boolean[][] col = new boolean[9][9];
boolean[][] row = new boolean[9][9];
boolean[][] place = new boolean[9][9];
public void solveSudoku(char[][] board) {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] == '.') {
continue;
}
int num = board[i][j] - '1';
row[i][num] = true;
col[j][num] = true;
place[i / 3 * 3 + j / 3][num] = true;
}
}
char[][]path=new char[9][9];
dfs2(board,path,col,row,place,0,0);
//dfs(board, 0, 0);
}
public boolean dfs(char[][] board, int i, int j) {
if (j == 9) {
return dfs(board, i + 1, 0);
} else if (i == 9) {
return true;
} else if (board[i][j] != '.') {
return dfs(board, i, j + 1);
}
for (int k = 0; k < 9; k++) {
if (col[j][k] || row[i][k] || place[i / 3 * 3 + j / 3][k]) {
continue;
}
board[i][j] = (char)('1' + k);
col[j][k] = true;
row[i][k] = true;
place[i / 3 * 3 + j / 3][k] = true;
if (dfs(board, i, j + 1)) {
return true;
}
board[i][j] = '.';
col[j][k] = false;
row[i][k] = false;
place[i / 3 * 3 + j / 3][k] = false;
}
return false;
}
//i 表示的是行数,j表示的是列数
public void dfs2(char [][]abroad,char[][]path,boolean[][] col,boolean[][] row,boolean[][] place,int i,int j)
{
System.out.println("--------------------------------");
do{
if (i==9)
{
System.out.println("最后一步");
for(int i2=0;i2<9;i2++)
{
for (int j2=0;j2<9;j2++)
System.out.print(path[i2][j2]);
System.out.println();
}
return;
}else if (j==9) //说明列到达边界
{
// dfs2(abroad,path,col,row,place,i+1,0);
i+=1;
j=0;
System.out.println("进入,i的值为"+i);
}// 下面暂时保留
while (abroad[i][j]!='.')
{
j++;
}
}while (i==9||j==9||abroad[i][j]=='.');
//col表示列,row代表行,place代表九宫格,path代表历史记录
for(int k=0;k<9;k++) {
if (col[j][k]||row[i][k]||place[i/3*3+j/3][k])
{
//如果已经存在这个数了 那么进行下一个
continue;
}
else{
//如果不存在这个数
int n2=k+1;
char n1 =(char) (n2+'0');
abroad[i][j]=(char)n1;
System.out.println("改变第"+i+"行"+"第"+j+"列,值为 "+abroad[i][j]);
path[i][j]=(char)n1;
col[j][k]=true;
row[i][k]=true;
place[i/3*3+j/3][k]=true;
dfs2(abroad,path,col,row,place,i,j+1);
//消除影响
abroad[i][j]='.';
path[i][j]='.';
col[j][k]=false;
row[i][k]=false;
place[i/3*3+j/3][k]=false;
}
System.out.print(i);
System.out.println(j);
}
return;
}
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号