逻辑回归

逻辑回归（Logistic Regression）是机器学习中十分常用的一种模型，属于广义线性模型。在互联网领域得到了广泛的应用，尤其是在广告系统中用来估计CTR。本文主要介绍逻辑回归的模型形式，求解策略和算法。接着介绍逻辑回归的最大似然估计，最后说明为什么逻辑回归要采用sigmoid函数做变换。

 

模型

我们知道，线性回归模型输出的是一个连续值，如果我们要输出的不是连续值，该怎么做呢？假设我们的输出只有 1 和 -1。

逻辑回归模型形式上是把线性回归模型做一个变换，让其输出是一个 0 到 1之间的数，假设我们的变换叫做 $g(z) $，然后在变换后的结果上定义一个决策函数，如果:

$\large y=1 \qquad \text{if} \qquad  g(z) > 0.5$

$\large y=-1 \qquad \text{if} \qquad  g(z) < 0.5$

其中 $z$ 就是我们前面讲到的线性模型：

$\large z = \mathbf{w}^T \mathbf{x} $

而变换采用了逻辑变换，也叫 sigmoid 变换，其形式为：

$\large g(z) = \frac {1}{1 + e^{-z}} $

通过上面几个式子进行一个简单的推导，我们的决策函数变为：

$\large y=1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} > 0$

$\large y=-1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} < 0$

最后我们的逻辑回归模型就变成：

$\large h_{\mathbf{w}}(\mathbf{x}) = g_{\mathbf{w}}(\mathbf{x}) = \frac {1}{1 + e^{- \mathbf{w}^T \mathbf{x}}} $

我们看看 sigmoid 函数有什么特点，从下面的图形可以看出，这个函数是个连续光滑函数，定义域是 $(-\infty, \infty)$，值域是 $[0,1]$，在 0 附近函数的区分度很高（$y$的值变化比较明显），越往两边，函数的区分度就越低（$y$的值变化越来越不明显）。

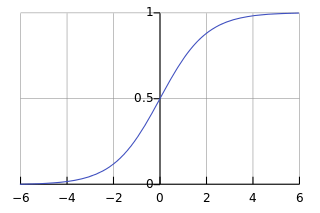
并且这个函数处处可导，其导数为：

$\large g^\prime = (\frac {1}{1 + e^{-z}})^\prime = \frac {e^{-z}} {(1 + e^{-z})^2} = g(z) \cdot (1- g(z)) $

其导数可以由自己本身表示。

而且：

$\large g(-z) = \frac {1}{1 + e^z} = 1 - g(z) $

$\large z=0, \qquad e^0=1, \qquad g(z) = 1/2 $

$\large z \to \infty, \qquad e^{-\infty} \to 0, \qquad g(z) = 1$

$\large z \to -\infty, \qquad e^{\infty} \to \infty, \qquad g(z) = 0$

为什么$sigmoid$函数比别的非线性函数有吸引力呢？ 做$sigmoid$变换的目的是把$(-\infty， \infty)$的取值范围(用$x$表示)映射到 $(0， 1)$ 范围内(用$y$表示): $h = y(x)$， 为此我们应该选择什么样的 $h$ 呢， $h$ 变换可以理解成对 $x$ 的一种编码， 当然$h$最好是双射， 意味着可以从$y$反解码得到$x$。 理论上满足双射的$h$可以有无穷多种， 该怎么选择呢？ 实际上双射是不可能的， 因为观测 $y$ 时不可避免的要引入误差， 即 $y = h(x) + \varepsilon $， 其中 $\varepsilon$ 为误差， 在有误差的情况下， $x$和$y$就不是一一映射了。 任何从 $y$ 反解码得到 $x$ 都是不可能的， 所以问题来了: 有没有一种映射$h$， 在有误差的情况下做到最优？ 通俗的讲， 就是寻找一个映射$h$， 在有观测误差$\varepsilon$的情况下， 最有的保持输入信号$x$的信息， 用信息学的语言描述就是$x$与$y$之间的互信息最大， 而$I(x， y)= H(y)- H(y|x)= H(y)- H(\varepsilon)$。 $x，y$的互信息由两项决定$H(y)=H(h(x))$ 和 $H(\varepsilon)$， 而其中第二项完全由误差决定， 我们控制不了。 第一项 $H(y)$是由映射$h$决定的， $H(y)$越大越好， 所以问题又变成: 给定取值范围$(0， 1)$， 熵 $H(y)$什么时候最大？ 答案就是$y$服从均匀分布时熵最大。 因此， 能把$x$映射成一个均匀分布的映射$h$是最优的。 当知道$x$的概率密度为$f(x)$时， 怎么样的变换能把 $x$ 变成均匀分布呢？ 还记得遇到多这样的面试题吗: 如何用$(0， 1)$的均匀分布生成任意的其他概率分布？ 答案是用一种叫 inverse cumulative distribution function 的变换方法。 而这里的问题正好和面试题相反， 我们要从任意分布生成均匀分布。 答案就是$f(x)$的累积分布函数$F(x)$就是最优的$h$。 想象一下正态分布的概率密度函数， 是一个倒置的钟形函数， 而它的累积分布函数是不是和 $sigmoid$ 函数长得很像？ 而现实中我们遇到的倒置钟形分布的信号又比比皆是。 注意: 对概率密度不是倒置钟形的信号， $sigmoid$变换不一定是最优的。

 

策略

有了逻辑回归模型的形式，我们仍然需要根据我们观测到的数据集求出模型里未知的 $\mathbf{w}$，为此我们仍然采用定义损失函数，并最小化损失函数的策略。此时我们不能用线性回归里采用的平方损失函数，因为此时在逻辑变换的基础上，改函数不再是一个凸函数，会给我们的极小化造成相当大的麻烦。为此，我们定义另外一个损失函数，逻辑斯谛损失（也叫交叉熵 Cross Entropy）:

$\large cost( h_{\mathbf{w}} (\mathbf{x}) ) = -\ln g(y \mathbf{w}^T \mathbf{x}) = -\ln (g(yz))$

我们先看看我们的的决策函数:

$\large y=1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} > 0$

$\large y=-1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} < 0$

检验一下我们的损失函数：

当 $y=1$时：

$\large \text{if} \qquad z \to \infty, \qquad g(yz) \to 1, \qquad cost \to 0$

$\large \text{if} \qquad z \to -\infty, \qquad g(yz) \to 0, \qquad cost \to \infty$

当 $y=-1$时：

$\large \text{if} \qquad z \to \infty, \qquad g(yz) \to 0, \qquad cost \to \infty$

$\large \text{if} \qquad z \to -\infty, \qquad g(yz) \to 1, \qquad cost \to 0$

 所以最后我们总的损失函数为：

$\large L(\mathbf{w}) = -\frac {1}{m} \sum_{i=1}^m \ln g(y \mathbf{w}^T \mathbf{x} ) =  -\frac {1}{m} \sum_{i=1}^m \ln ( 1 + e^{-y^i \mathbf{w}^T \mathbf{x}^i} ) $

 

算法

我们仍然采用梯度下降来求解 $\mathbf{w}$，因为梯度下降收敛太慢，一般工程上都不会直接采用梯度下降来解这个问题，工程上会采用拟牛顿法比如LBFGS来求解（具体原理请参考），这里为了简单，用梯度下降示例。

先求 $L(\mathbf{w})$ 的梯度向量：

$\large \nabla (\mathbf{w}) = \frac {1}{m} \sum_{i=1}^m g(-y^i \mathbf{w}^T \mathbf{x}^i )(-y^i \mathbf{x}^i) $

其中 $m$ 为训练数据集的大小。

逐步更新 $\mathbf{w}$：

$\large \mathbf{w} := \mathbf{w} - \alpha \nabla (\mathbf{w}) $

拟牛顿法(BFGS)和LBFGS的求解请参考数学基础之微积分里相关的部分.

 

最大似然估计

上面提到了逻辑斯谛损失，为什么我们要定义这样一个损失呢？我们从另一方面来解释，我们假设我们的模型最后分别以一定概率输出 1 和 -1， 假设输出 1 的概率是 $p$， 输出 -1 的概率是 $1-p$，即：

$\large p(y=1|\mathbf{x}) = p, p(y=-1|\mathbf{x})=1-p $

$p/1-p$ 我们称之为几率，$\ln(\frac {p} {1-p})$ 我们称之为对数几率，我们建立下面这样一个线性模型来模拟这个对数几率：

$\large \ln(\frac {p} {1-p}) = \mathbf{w}^T \mathbf{x}$

然后很快就能求出：

$\large p = \frac {1}{1 + e^{-\mathbf{w}^T \mathbf{x}}} $

所以：

$\large p(y=1|\mathbf{x}) = \frac {1}{1 + e^{-\mathbf{w}^T \mathbf{x}}} = \frac {1}{1 + e^{-y \mathbf{w}^T \mathbf{x}}}$

$\large p(y=-1|\mathbf{x}) = 1 - \frac {1}{1 + e^{-\mathbf{w}^T \mathbf{x}}} = \frac {1}{1 + e^{-y \mathbf{w}^T \mathbf{x}}}$

所以无论$y=1$还是$y=-1$, 概率都可以写成统一的形式:

$\large p(y|\mathbf{x}) = \frac {1}{1 + e^{-y \mathbf{w}^T \mathbf{x}}}$

 

下面我们用最大似然估计来估计 $\mathbf{w}$，假设我们的训练数据集为：

$\large D={(\mathbf{x}^1, y^1),(\mathbf{x}^2, y^2),\ldots,(\mathbf{x}^m, y^m)}$

生成这样一个数据集的概率为：

$\large p(D) = p(\mathbf{x}^1)p(y^1 | \mathbf{x}^1) p(\mathbf{x}^2)p(y^2 | \mathbf{x}^2) \ldots p(\mathbf{x}^m)p(y^m | \mathbf{x}^m) = \Pi_{i=1}^m p(\mathbf{x}^i)  \Pi_{i=1}^m p(y^i | \mathbf{x}^i)$

将我们的模型概率的统一形式代进去：

$\large p_{\mathbf{w}}(D) = \Pi_{i=1}^m p(\mathbf{x}^i)  \Pi_{i=1}^m \frac {1}{1 + e^{-\mathbf{w}^T \mathbf{x}^i}}   $

我们要找到一个 $\mathbf{w}$, 让上面的式子最大, 其中第一项连乘跟 $\mathbf{w}$ 无关, 两边同时取对数:

$\large max_{\mathbf{w}} \ln p_{\mathbf{w}}(D) = max_{\mathbf{w}}  \sum_{i=1}^m  \ln \frac {1}{1 + e^{- y \mathbf{w}^T \mathbf{x}^i}} = max_{\mathbf{w}} \sum_{i=1}^m \ln (1 + e^{-y \mathbf{w}^T \mathbf{x}^i}) = min_{\mathbf{w}} \sum_{i=1}^m -\ln (1 + e^{-y \mathbf{w}^T \mathbf{x}^i}) $

得到了跟上面定义损失函数, 然后极小化损失函数一样的结论.

 

参考资料

[1]: http://en.wikipedia.org/wiki/Sigmoid_function

[2]: Machine Learning https://class.coursera.org/ml-2012-002

[3]: 机器学习基石 https://class.coursera.org/ntumlone-002

[4]: Pattern recognization and machine learning http://research.microsoft.com/%E2%88%BCcmbishop/PRML