2019面向对象程序设计第一单元总结
一.三次作业的设计思路
Ⅰ.仅含常数和幂函数的多项式求导
(1)思路一:WF判断与分项结合,避免大正则爆栈问题
第一次作业中,多项式的结构具有极强的规律性,所以不少同学想到用正则表达式匹配整串,但忽略了大正则存在回溯次数过多可能会导致爆栈。因此正确的处理策略之一是,单独处理输入中的空格,正负号以及非法字符,然后用正则匹配表达式中的每一项,得到的所有项相加,若与原表达式不相同,则判为“WRONG FORMAT!”,否则,则输出求导结果。
正则匹配处理空格与符号后的每一项:
Pattern pattern = Pattern.compile("([-+]+(([-+]?(\\d+\\*)?x(\\^[-+]?\\d+)?)|([-+]?\\d+)))");
然后用Matcher中的find()函数实现分离每一项,用Matcher中的group()函数实现项处理。
(2)思路二:用ArrayList、LinkedList或HashMap实现动态插入新项
笔者在第一次作业中采用的是利用泛型的LinkedList实现
public class PolyHandler {
//利用链表构造求导后的新多项式
private LinkedList<String[]> polynomial;
//构造函数
PolyHandler(LinkedList<String[]> polynomial) {
this.polynomial = polynomial;
}
重点:在动态添加元素的过程中,实现同类项的合并,能够大大减少优化复杂度。
笔者利用PolyHandler类中的merge函数实现求导后多项式合并新项
void merge(String[] item)
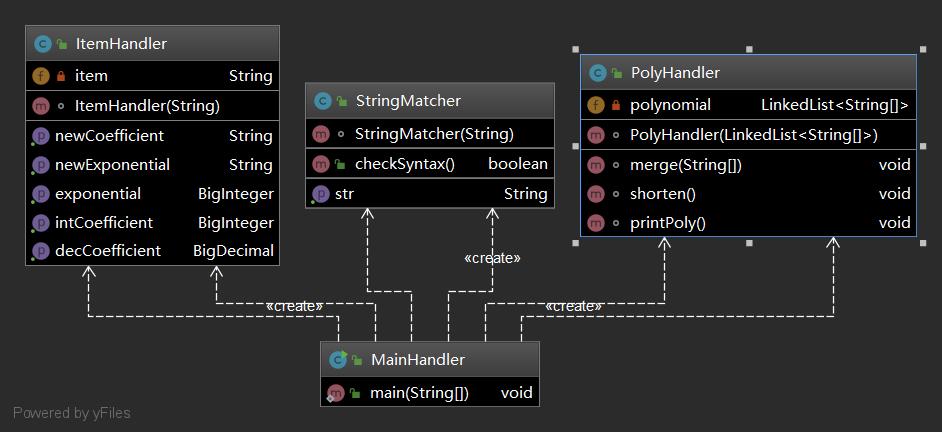
下图为第一次作业我的类图
StringMatcher用于初步判断输入是否合法
ItemHandler为项处理类
PolyHandler为多项式处理类
MainHandler为主类
Ⅱ.仅含常数、幂函数和三角函数的多项式求导
(1)思路一:本次作业仍可利用正则进行分项
笔者认为,第二次作业相比第一次多项式求导作业而言,在处理非法输入与求导方面对整体架构的改变不大,因此笔者沿用了第一次作业的设计,复用了较多的类。
正则分项:
Pattern pattern = Pattern.compile("[-+](\\d+|(x(\\^[-+]?\\d+)?)|" +
"(sin\\(x\\)(\\^[-+]?\\d+)?)|(cos\\(x\\)(\\^[-+]?\\d+)?))" +
"(\\*[-+]?(\\d+|(x(\\^[-+]?\\d+)?)" +
"|(sin\\(x\\)(\\^[-+]?\\d+)?)|(cos\\(x\\)(\\^[-+]?\\d+)?)))*");
emmm......看上去是不是很复杂呢,在第二次作业我们已经可以上递归下降分析了!
(2)思路二:用HashMap处理多个Key,化简时有巨大优势
自定义一个类,包含多个Key,将这个类作为HashMap的Key类型,并实现这个类的哈希函数和相等性判定函数。
1.哈希函数
int hashcode()
2.相等性判定函数
boolean equals(object obj)
下图是笔者自己设计的HashKey类中重写的核心方法

注:在第二次作业中,利用HashMap实现同类项的合并相比ArrayList与LinkedList有更大优势。
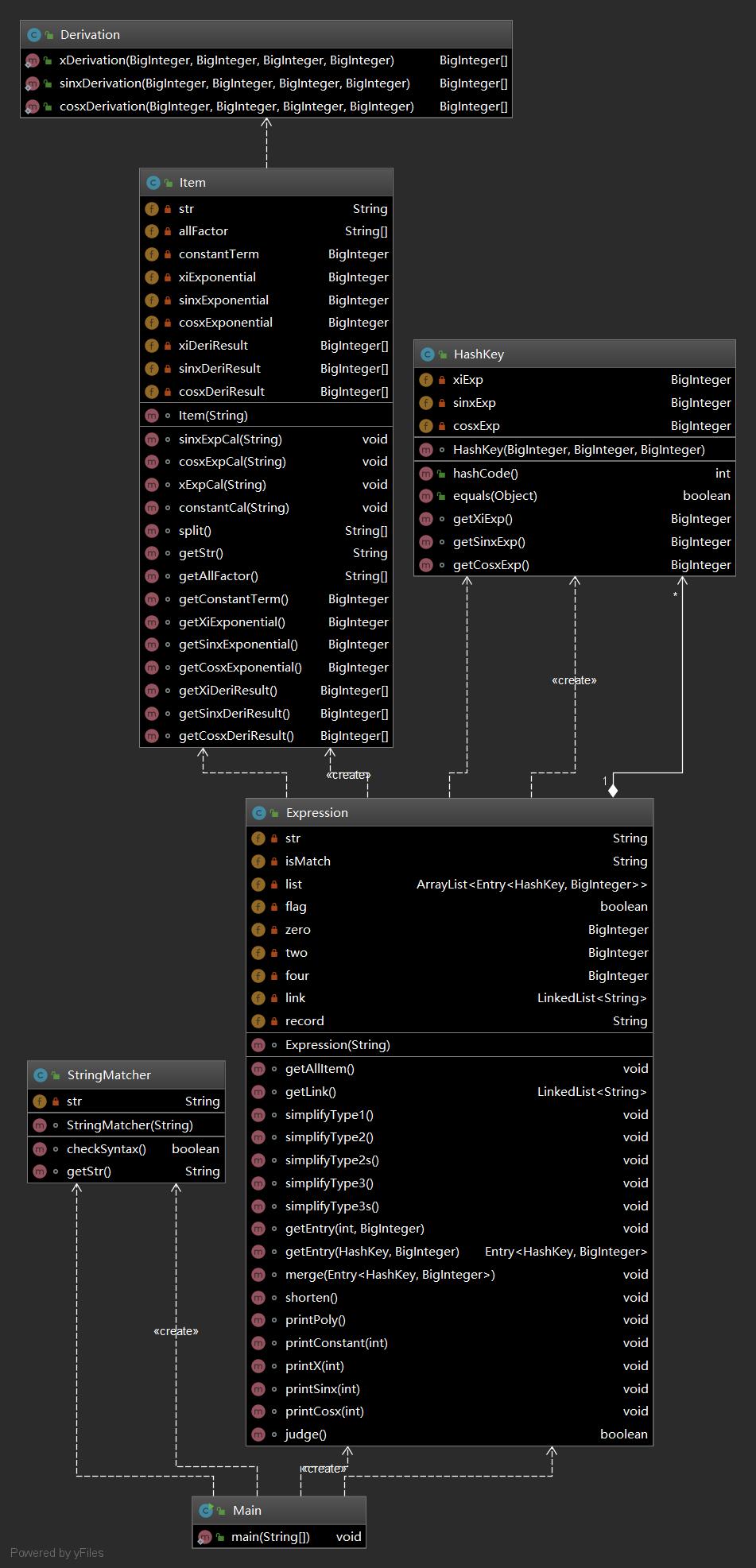
下图为我第二次作业的类图
StringMatcher类用于判断输入是否合法
HashKey类为自己设计构造的HashMap的Key类型
Expression类为表达式处理类
Item类为项处理类
Derivation类为求导类
III.包含常数、项、幂函数与嵌套三角幂函数多项式的求导
核心思想——递归下降分析法:表达式由项构成,项由因子构成,因子的种类可以是表达式,幂函数,常数项,三角函数类。
1.表达式:读取项,用LinkedList存储项:
LinkedList<Term> parseExpression()
2.项:读取因子,用LinkedList存储因子:
Term parseTerm()
3.因子
//外包函数,分析因子种类,然后分种类爬取因子
Factor parseFactor()
//获取常数项因子
Factor getConstantFactor()
//获取幂函数因子
Factor getXFactor()
//获取正弦函数因子
Factor getSinxFactor()
//获取余弦函数因子
Factor getCosxFactor()
//获取表达式因子
Factor getExpressionFactor()
为使逻辑清晰,可把因子种类定义为枚举类型。
public enum FactorType {
constant,x,sin,cos,expression
}
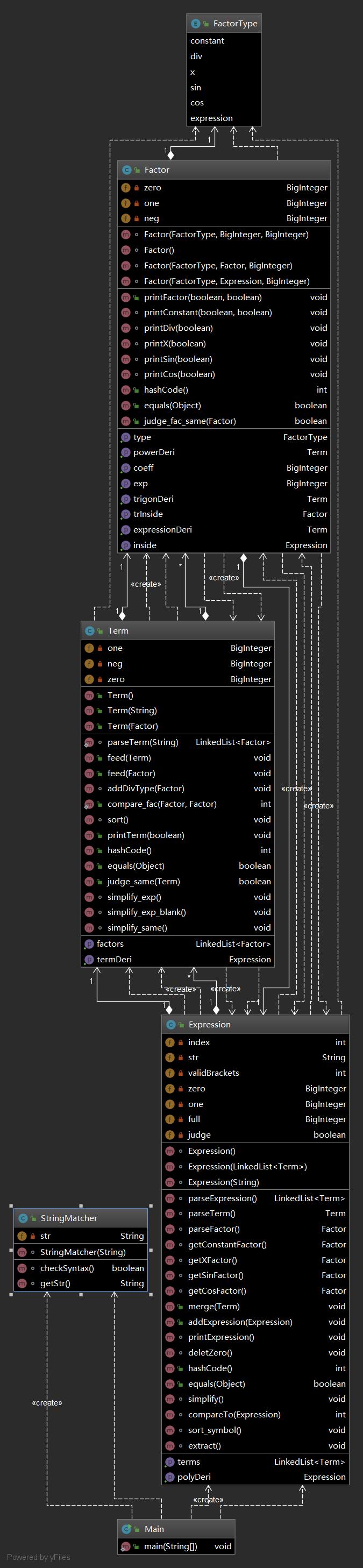
下图为第三次作业我的类图
StringMatcher类用于判断输入格式是否为正确格式
Expression类为表达式处理类
Term类为项处理类
Factor类为因子处理类
FactorType枚举类型定义了因子类型
二.优化策略简介
笔者会在另一篇博文中对优化策略进行详解,在此仅说下整体思路。
题外话,笔者在三次作业的优化中均取得了还不错的成绩,第一次作业满分,第二次作业第11名,第三次作业前10名
1).第一次作业优化要点:
①合并同类项
②正项前移
2).第二次作业优化要点:
①合并同类项
②利用三角函数公式简化(主要采用了以下四类公式):
1° sin(x)^2 + cos(x)^2 = 1
2° 1-sin(x)^2 = cos(x)^2
3° 1-cos(x)^2 = sin(x)^2
4° sin(x)^4 - cos(x)^4 = sin(x)^2 - cos(x)^2
③正项前移
3).第三次作业优化要点:
笔者认为,第三次作业的优化重点不在于利用三角函数公式简化,而在于在可控时间复杂度下利用递归下降实现同类项的合并,这便需要重写Expression类、Term类、Factor类的hashcode()和equals()函数
三.综合三次作业的方法复杂度的分析
第一次作业:
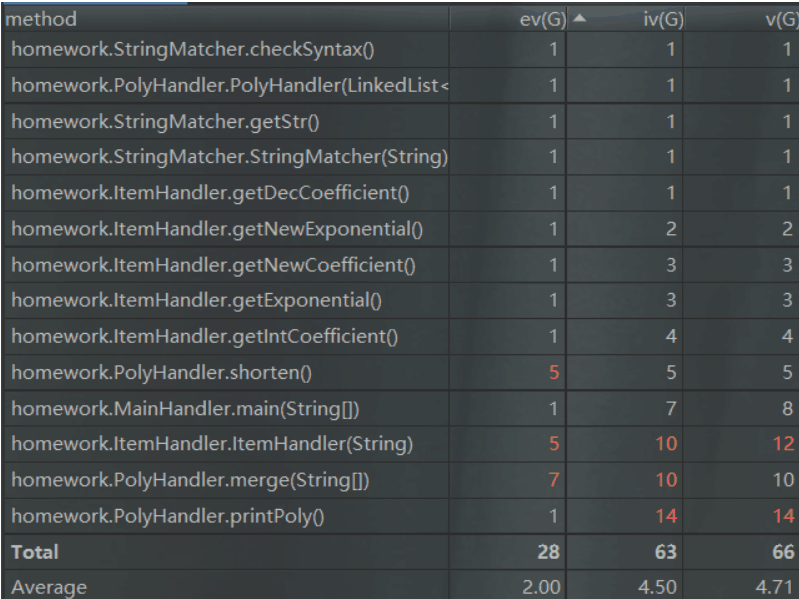
第二次作业:
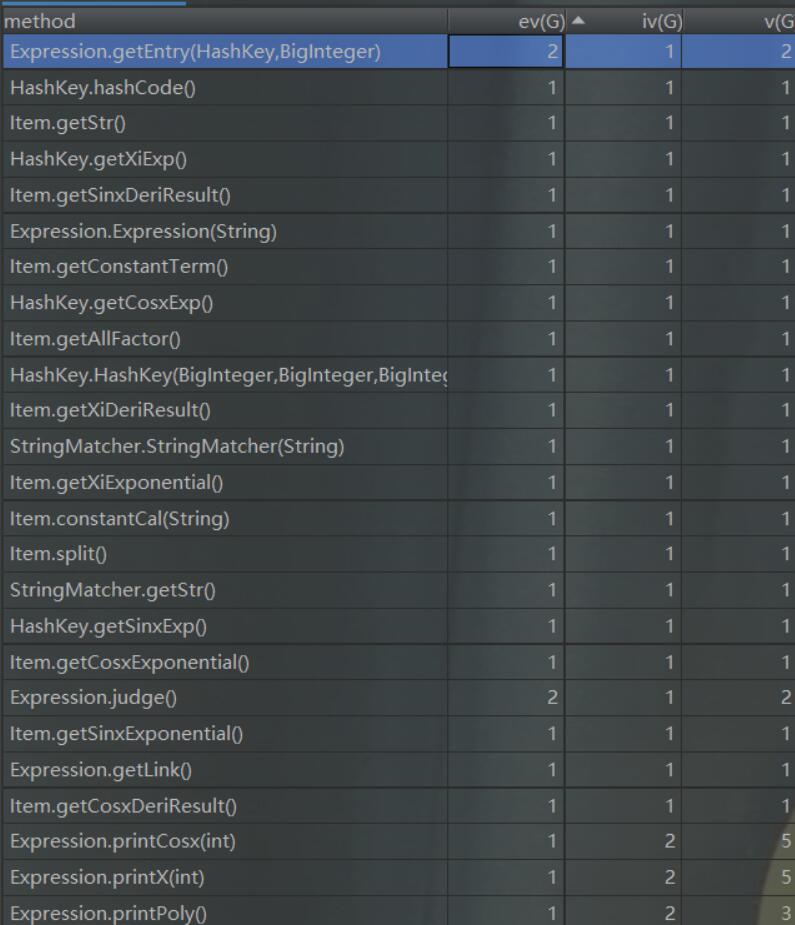
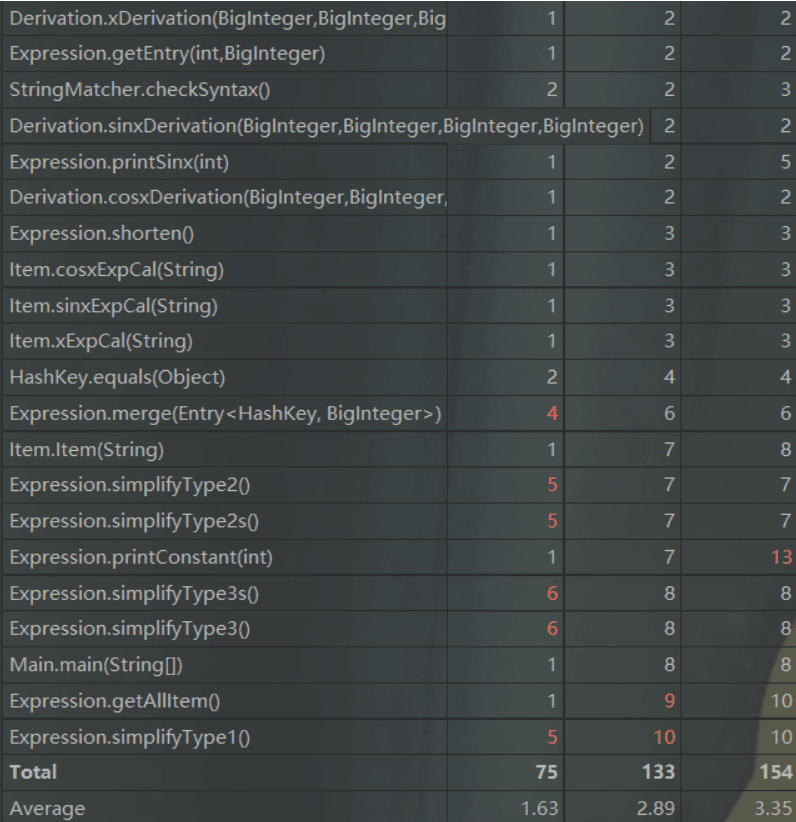
第三次作业:
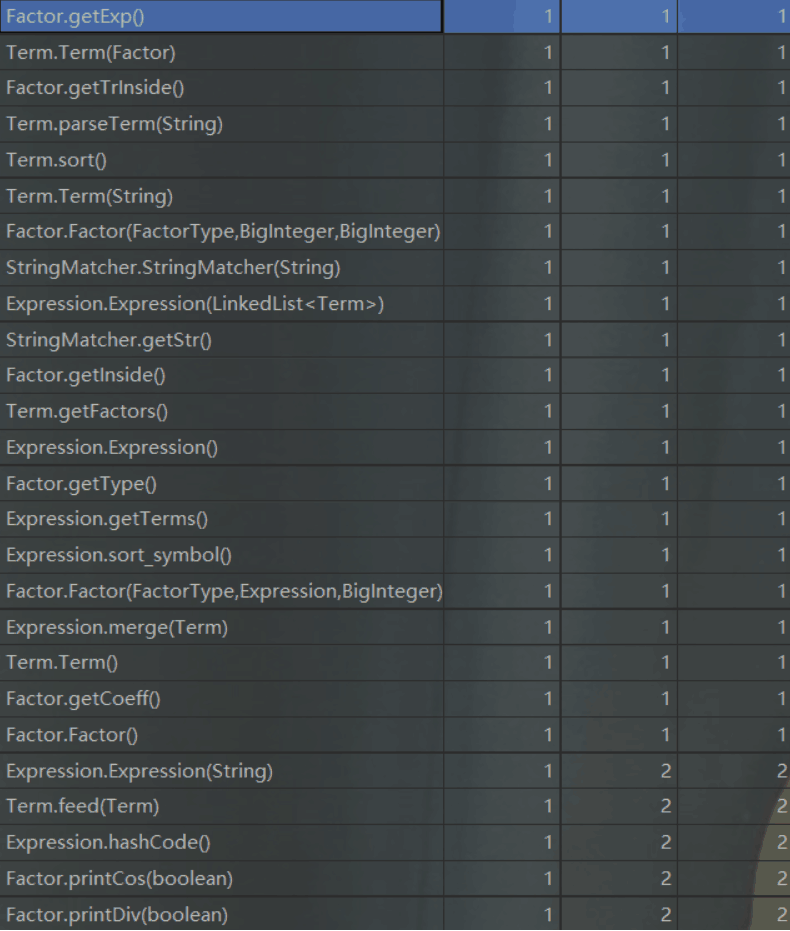
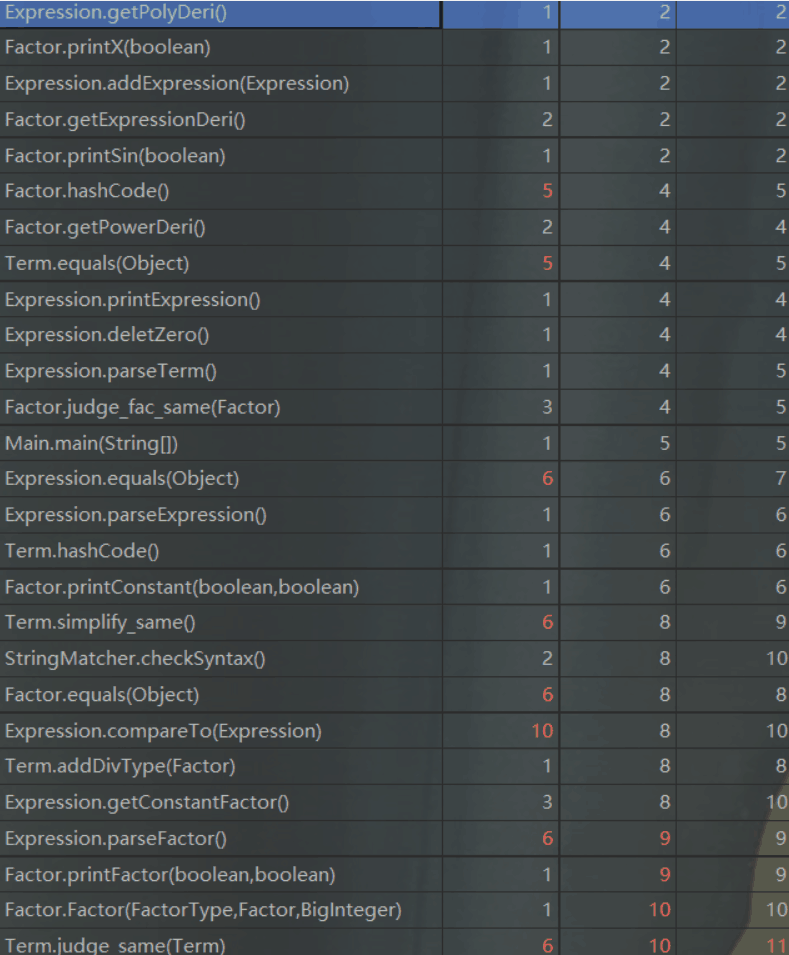
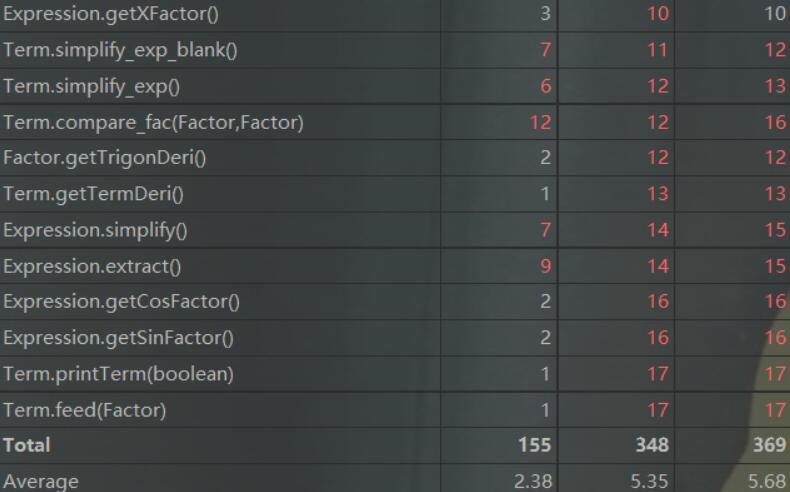
可以看出,随着三次作业的层层递进,工程的方法数目与方法复杂度均在上升。由于二、三次作业的优化相对复杂,故我在相应的类中实现了较多复杂度较高的方法来进行相应的优化,具体方法逻辑可参考类图。
四.Bug分析
三次作业我的强测全部通过,均没有出现bug,加上优化分,笔者在三次作业中的强测得分分别为100分、99.2839分、96.7647分。
但在第三次作业中,我被别的玩家hack了一个点,系我在化简过程中一个if语句判断失误,去除了三角函数中表达式因子的括号,导致输出格式有问题。这也告诫我,在优化过程中,一定要考虑全面。
五.高效Debug和Hack策略分析
笔者认为,其实要想成为OO互测的顶级玩家,必须要拥有一台自己编写的评测机,千万不要偷懒。
(1)构建自己的“强测”评测机(全面覆盖):
① 自动生成随机表达式串
② 让本组成员的程序互拍,寻找不同结果。
③ 判断错误结果的来源、错误结果的种类(即Wrong Format Error、Wrong Value Error还是Wrong Derivative Error),并输出到指定文件
下图是用Python实现的第三次作业的评测机。
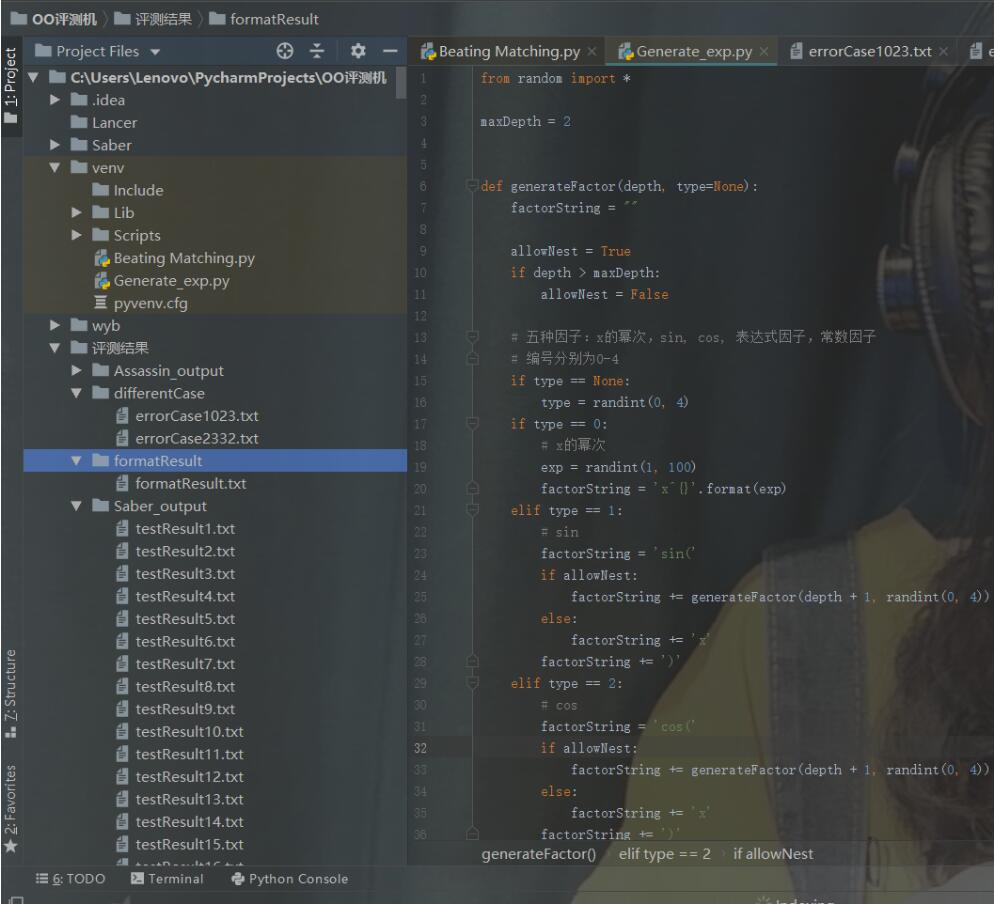
(1)精心构造测试样例(重点针对):
评测机生成的数据太随机,因此往往有些bug会疏漏掉,需要自己读懂评测屋内的代码,并分析其架构和逻辑上的失误,并构造相应样例。
比如第二次作业的一个针对优化的典型hack样例:
x*sin(x)^4*cos(x)^-4+x*sin(x)^5*cos(x)^-5+x*sin(x)^2*cos(x)^-2+x*cos(x)^-3+x*sin(x)^6*cos(x)^-6
第三次作业的一个典型hack样例
cos((((-+((((sin(x)))))))))
六.Applying Creational Pattern
工厂模式与抽象工厂
对于本次作业可以使用工厂模式来创建表达式,项,因子,我们只需定义一个创建对象的接口,让实现了该接口的子类自己决定实例化哪一个工厂类。在我们明确地计划不同条件下创建不同实例时,工厂模式将十分管用。
抽象工厂模式是围绕一个超级工厂创建其他工厂。在抽象工厂模式中,接口是负责创建一个相关对象的工厂,不需要显式指定它们的类。每个生成的工厂都能按照工厂模式提供对象,这样我们就不用花费时间在选择接口上了。
七.总结与展望
北航的OO课正在不断变好,感谢老师、助教和为其他为这门课默默付出的人。我会再接再厉,不断提升自己的分析能力和代码能力。



