题目:
扔 n 个骰子,向上面的数字之和为 S。给定 Given n,请列出所有可能的 S值及其相应的概率。
给定
n = 1,返回[ [1, 0.17], [2, 0.17], [3, 0.17], [4, 0.17], [5, 0.17], [6, 0.17]]。
方法一
概率问题最简单有效的方法当然是枚举啊,况且现在的计算机这么优秀。
n个骰子一起投掷,先列出所有可能的结果,然后求和,计数,最后算概率;
首先枚举需要的空间先给上
int[][] matrix = new int[(int) Math.pow(6, n)][n];
然后进行n重循环,枚举所有的可能情况
int speed = 0; // 变化的步长 int count = 0; // 计数器 int point = 0; // 当前要写入的数值 for (int i = 0; i < n; i++) { speed = (int) Math.pow(6, i); count = 0; point = 0; for (int j = 0; j < MAX; j++, count++) { if (count == speed) { count = 0; point++; } matrix[j][i] = (int) (point % 6 + 1); } }
然后就获得了所有的情况,而且这些情况都是等概率的;
之后就就很容易了,
然而。。。
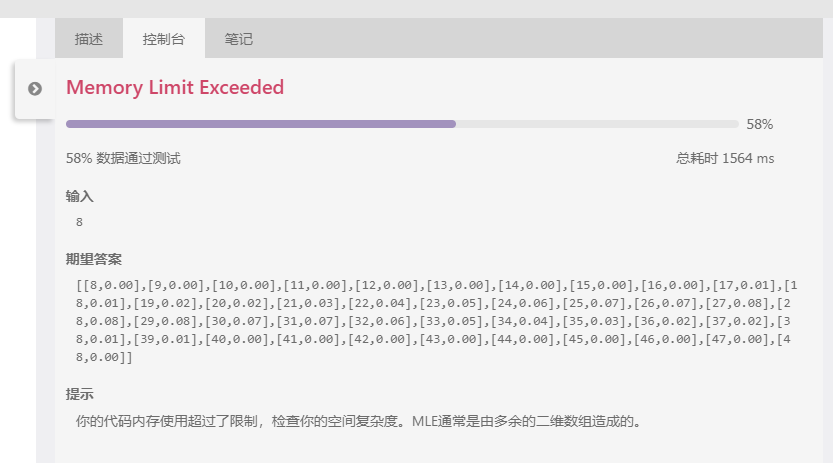
运行到 n = 8 的时候崩了。。。
把 int变成 short,再改成 char,都不好使,,,额,这个出题人不想让我们用枚举。。。
是的后面当 n = 15 时,本地的IDE页崩了;
Exception in thread "main" java.lang.OutOfMemoryError: Requested array size exceeds VM limit
所以这题要用到一些算法知识。。。
方法二
再此向大家介绍全概公式:
全概率公式为概率论中的重要公式,它将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。内容:如果事件B1、B2、B3…Bn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Bi)大于0,则对任一事件A有P(A)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn)。或者:p(A)=P(AB1)+P(AB2)+...+P(ABn)),其中A与Bn的关系为交)。
这个题目正好就是这样
投 6个骰子点数和为 25的概率 = 投 6个骰子点数和为 25并且最后一个点数为1的概率 + 投 6个骰子点数和为 25并且最后一个点数为2的概率
+ 投 6个骰子点数和为 25并且最后一个点数为3的概率 + ... + 投 6个骰子点数和为 25并且最后一个点数为6的概率;
换言之:
投 6个骰子点数和为 25的概率 = 投 前5个骰子点数和为 24并且最后一个点数为1的概率 + 投 前5个骰子点数和为 23并且最后一个点数为2的概率
+ 投 前5个骰子点数和为 22并且最后一个点数为3的概率 + ... + 投 前5个骰子点数和为 19并且最后一个点数为6的概率;
得出普遍结论:
投 n个骰子点数和为 Sum的概率 = 投 前 n-1个骰子点数和为 Sum-1并且最后一个点数为1的概率 + 投 前 n-1个骰子点数和为 Sum-2并且最后一个点数为2的概率
+ 投 前 n-1个骰子点数和为 Sum-3并且最后一个点数为3的概率 + ... + 投 前 n-1个骰子点数和为 Sum-6并且最后一个点数为6的概率;
举例检验:
投 2个骰子点数和为 6的概率 = 投 第一个骰子点数为 5并且第二个点数为1的概率(1/6 * 1/6) + 投 第一个骰子点数为 4并且第二个点数为2的概率(1/6 * 1/6)
+ 投 第一个骰子点数为 3并且第二个点数为3的概率(1/6 * 1/6) + 投 第一个骰子点数为 2并且第二个点数为4的概率(1/6 * 1/6)
+ 投 第一个骰子点数为 1并且第二个点数为5的概率(1/6 * 1/6) + 投 第一个骰子点数为 0并且第二个点数为6的概率(0/6 * 1/6) = 5/36;
投 2次的概率可以从投 1次的概率中得出,投 3次的概率可以从投 2次的概率中得出,投 4次的概率可以从投 3次的概率中得出...
所以我们可以从第二次一直计算到第 n次,
由于概率的分母为所有可能出现的情况的总数为定值:为 6的n次方;
所以我们可以先只记录可能种类的次数,最后再算概率;
double[][] matrix_II = new double[100][1000]; for (int i = 1; i < matrix_II.length; i++) { for (int j = 0; j < matrix_II[0].length; j++) { matrix_II[i][j] = 0; } } matrix_II[1][1] = matrix_II[1][2] = matrix_II[1][3] = 1; matrix_II[1][4] = matrix_II[1][5] = matrix_II[1][6] = 1; for (int i = 2; i <= n; i++) { for (int j = i; j <= 6 * i; j++) { double sum2 = 0; for (int k = j - 6; k <= j - 1; k++) { if (k > 0) { sum2 += matrix_II[i - 1][k]; } } matrix_II[i][j] = sum2; } }
格式化后,
第一层循环:从第二次到第 n次;
第二层循环:n次投掷可能的结果:n到 6n;
第三层循环:本次的概率与上次的 6种情形的概率有关;
循环完毕即得到了一个从1到 n次的投掷情况的次数矩阵;
然后只要在最后遍历一次最后一趟作为输出就行了;
附上程序:
public class Solution { /** * @param n an integer * @return a list of Map.Entry<sum, probability> */ public List<Map.Entry<Integer, Double>> dicesSum(int n) { // Write your code here // Ps. new AbstractMap.SimpleEntry<Integer, Double>(sum, pro) // to create the pair double MAX = Math.pow(6, n); double[][] matrix_II = new double[100][1000]; for (int i = 1; i < matrix_II.length; i++) { for (int j = 0; j < matrix_II[0].length; j++) { matrix_II[i][j] = 0; } } matrix_II[1][1] = matrix_II[1][2] = matrix_II[1][3] = 1; matrix_II[1][4] = matrix_II[1][5] = matrix_II[1][6] = 1; double sum2 = 0; for (int i = 2; i <= n; i++) { for (int j = i; j <= 6 * i; j++) { sum2 = 0; for (int k = j - 6; k <= j - 1; k++) { if (k >= i - 1) { sum2 += matrix_II[i - 1][k]; } } matrix_II[i][j] = sum2; } } List<Map.Entry<Integer, Double>> list = new ArrayList<>(); for (int i = n; i <= 6 * n; i++) { AbstractMap.SimpleEntry<Integer, Double> entry = new AbstractMap.SimpleEntry<>(i, matrix_II[n][i] / MAX); list.add(entry); } return list; } }
需要注意的是当程序运行到 n=15 时,数值已经大过 Int类型了;
哟。
进阶 方法三
上面的方法二应该是最有效的方法了,但似乎感觉还是有点不让人满意,求 n的概率必须把前面的概率都算一遍;
有没有一种直接就去找 n的算法呢?
有啊,因为我们平时的思考方式肯定不是从 1开始推啊;
常见的问题:投掷 3个骰子向上的点数和为 7的概率为多少?
肯定是推:有115(3),124(6),133(3),223(3),3+6+3+3=15,概率为15/36 = 5/12;
我们也可以这样啊,分别直接去求 n到 6n的概率;
1.获取去重全排列的个数;
2.获取关键的数组(如115,124等);
首先是简单的获取第一个关键数组,即和为 sum,各个位置的数值从左往右递增;
int[] arr = new int[n]; for (int i = 0; i < n - 1; i++) { arr[i] = 1; } arr[n - 1] = sum - n + 1; for (int i = 1; i < n; i++) { if (arr[n - i] > 6) { arr[n - i - 1] = arr[n - i - 1] + arr[n - i] - 6; arr[n - i] = 6; } }
从倒数第二位开始,进行判断,替换和重新构造;
哈哈,之后就不会写了。。。
for (int i = n - 2; i >= 0; i--) { // 从倒数第二个开始 while (arr[i] + 1 < 6 && arr[i + 1] - 1 > 0 && arr[i + 1] - arr[i] >= 2) { arr[i] += 1; arr[i + 1] -= 1; for (int index = 0; index < n; index++) { System.out.print(arr[index]); } System.out.println(); } }
大致是这么个结构。。。但还少进位,重构等功能;
我在这里就阵亡了,诸位算法大师,数学家,就拜托你们了;
重置 方法一
谁说枚举不能用了。。。只要不占用那么多的空间不就好了;
上程序
public class Solution { /** * @param n an integer * @return a list of Map.Entry<sum, probability> */ public List<Map.Entry<Integer, Double>> dicesSum(int n) { // Write your code here // Ps. new AbstractMap.SimpleEntry<Integer, Double>(sum, pro) // to create the pair double MAX = Math.pow(6, n); double[] sum_array = new double[6 * n + 1]; for (int i = 0; i < sum_array.length; i++) { sum_array[i] = 0; } int[]matrix = new int[n+1]; for (int i = 1; i < matrix.length; i++) { matrix[i] = 1; } int sum; while (true) { sum = 0; for (int b = 1; b <= n; b++) { sum += matrix[b]; } sum_array[sum]++; matrix[n]++; for (int i = n; i > 0; i--) { if(matrix[i] == 7) { matrix[i-1]++; matrix[i] = 1; } } if(matrix[0] > 0) { break; } } List<Map.Entry<Integer, Double>> list = new ArrayList<>(); for (int i = n; i <= 6 * n; i++) { AbstractMap.SimpleEntry<Integer, Double> entry = new AbstractMap.SimpleEntry<>(i, sum_array[i] / MAX); list.add(entry); } return list; } }
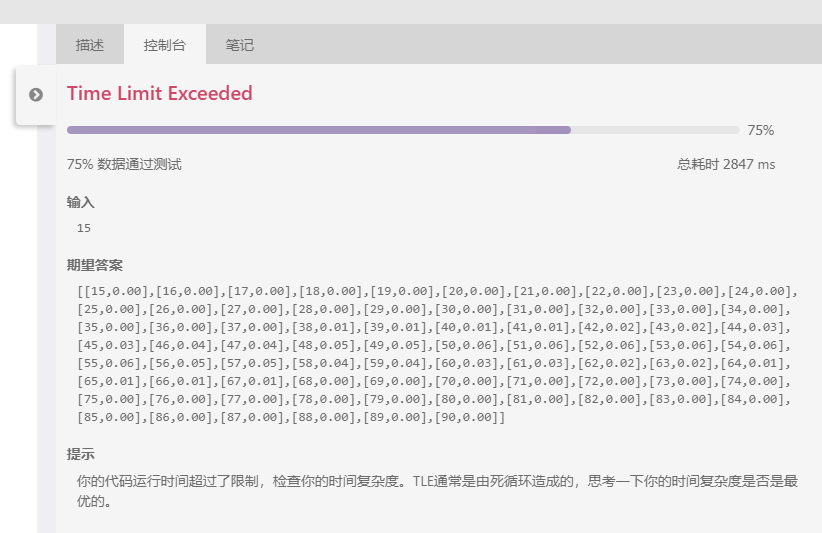
就想到了。。。枚举超时了。。。
行了,不挣扎了。




